МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
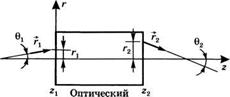
Рассмотрим луч света, пропускаемый или отражаемый оптическим элементом, действие которого обратимо по отношению к входящему и выходящему пучкам и не зависит от поляризации света (например, линза или зеркало) [1]. Обозначим через г оптическую ось этого элемента (например, линию, проходящую через центры кривизны двух сферических поверхностей линзы). Предположим, что луч распространяется преимущественно в направлении оси г в плоскости, содержащей эту ось. Лучевой вектор гх в данной плоскости на входе г = гх этого оптического элемента (рис. 4.1) можно охарактеризовать двумя параметрами, а именно, его радиальным смещением ^(^х) и отклонением по углу от оси г. Точно так же лучевой вектор г2 в данной плоскости на
|
|
|
Рис. 4.1 Матричное представление распространения луча через обобщенный оптический элемент |
Выходе z — г2 можно охарактеризовать его радиальным смещением r2(z2) от оси г и отклонением по углу 02. Отметим, что как для входящего, так и для выходящего лучей используется одна и та же ось значений г, ориентированная так, как показано на рис. 4.1. Соглашение о знаках углов таково: величина угла считается положительной, если вектор г нужно вращать по часовой стрелке для того, чтобы он оказался направлен вдоль положительного направления оси г. Так, например, на рис. 4.1 величина 0Х положительна, тогда как величина 02 — отрицательна.
В приближении параксиальных пучков лучей (англ. paraxial-ray approximation) предполагается, что угловые отклонения 0 достаточно малы, чтобы выполнялись приблизительные соотношения sin 0 = tan 0 = 0. В этом случае параметры на выходе (г2, 02) и на входе (гх, 0Х) оказываются связанными некоторым линейным преобразованием. Если ввести обозначения 0Х = (drx /dzi)2l - г/ и02 = (dr2/dz2)Z2 = г', то можно записать:
|
|
||
|
(4.2.2) |
![]() Где А, Б, С и И — константы, характерные для данного оптического элемента. Таким образом, в матричном представлении соотношения (4.2.1) естественно записать в виде:
Где А, Б, С и И — константы, характерные для данного оптического элемента. Таким образом, в матричном представлении соотношения (4.2.1) естественно записать в виде:
|
Г2 |
А |
В |
>1 |
||
|
4 |
С |
D |
Г{ |
Где ABCD-матрица, или лучевая матрица, полностью характеризует данный оптический элемент в приближении параксиальных пучков лучей.
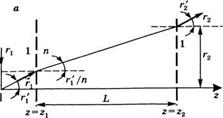
В качестве первого и самого простого примера рассмотрим распространение луча на расстояние Az = L в свободном пространстве среды с показателем преломления п (см. рис. 4.2а). Если плоскости на входе и на выходе расположены прямо на ее границах, в среде с единичным показателем преломления, то, используя закон Снеллиуса, в параксиальном приближении получаем:
Г2 =/j +Lr[/n, (4.2.3а)
Г2=г{, (4.2.36)
Так что соответствующая ABCD-матрица имеет вид:
1 L/n
0 ! • (4.2.4)
|
Б |
*1 |
1 r'i |
||
|
Р |
Л |
К < |
• | * ? | |
|
|
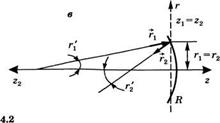 Расчет АВС1)-матрицы для: (а) распространения в свободном пространстве,
Расчет АВС1)-матрицы для: (а) распространения в свободном пространстве,
(б) распространения через тонкую линзу, (в) отражения от сферического зеркала
В качестве следующего примера рассмотрим прохождение луча сквозь линзу с фокусным расстоянием f (величина f берется положительной для фокусирующей линзы). Очевидно, что для тонкой линзы (см. рис. 4.2б)
|
Г2 = Г 1* |
![]() (4.2.5а)
(4.2.5а)
Второе соотношение получается из хорошо известной формулы геометрической оптики, а именно (1/р) + (1/q) = (1//), и учета того факта, что p = r1/r{y8iq = - r2/r2. Используя также соотношение (4.2.5а), получаем:
|
(4.2.56) |
![]() Г2=~(1/ИП+Г{.
Г2=~(1/ИП+Г{.
В соответствии с (4.2.5), АВСВ-матрица в этом случае равна:
|
(4.2.6) |
![]() 1 О 1// 1*
1 О 1// 1*
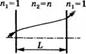
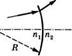
В качестве третьего примера рассмотрим отражение луча сферическим зеркалом с радиусом кривизны II (величина Я берется положительной для вогнутого зеркала). В этом случае плоскости и г2 выбирают совпадающими и расположенными непосредственно перед зеркалом, а положительное направление оси г считают одним и тем же для падающего и отраженного лучей (рис. 4.2в). За положительное направление оси г принимают направление слева направо для падающего луча и справа налево для отраженного. Угол для падающего луча положителен, если вектор гх нужно вращать по часовой стрелке для того, чтобы он оказался направлен вдоль положительного направления оси г19 тогда как угол для отраженного луча положителен, если вектор г2 нужно вращать против часовой стрелки для того, чтобы он оказался направлен вдоль положительного направления оси г2. Например, на рис. 4.2в величина г{ положительна, а величина г2'— отрицательна. При этих условиях лучевая матрица для вогнутого зеркала с радиусом кривиз-
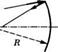
Лучевые матрицы для некоторых простых случаев
|
|||
|
|||
|
|||
|
|
||
|
|||

|
П |
А Ві |
П |
|
|
Г( |
Сі а |
Г{ |
|
|
Г2 |
-А-2 В2 |
П |
|
|
4 |
@2 Ог |
Г! |
|
(4.2.9) (4.2.10) |
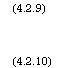
Если вместо вектора в правой части (4.2.10) подставить выражение (4.2.9), то получим:
|
А2 С2 В‘2 |
|
А, В1 С А |
|
|
Рис. 4.3
Распространение луча через три различные плоскости, когда известны матрицы для распространения луча между
ПЛОСКОСТЯМИ 2 = 21И2 = 2(
|
Г=2і 2=22 |
![]() И ПЛОСКОСТЯМИ 2 = 2гИ2 = 22
И ПЛОСКОСТЯМИ 2 = 2гИ2 = 22
Таким образом, полную АВС1)-матрицу для составной системы можно получить перемножением АВСХ>-матриц для отдельных ее компонент. Отметим, что порядок, в котором матрицы входят в такое произведение, противоположен порядку пересечения соответствующих элементов световым лучом.
В качестве первого и, в некотором смысле, тривиального примера использования полученного результата рассмотрим распространение луча в свободном пространстве среды с показателем преломления п на расстояние Ь19 за которым снова следует такое же распространение в той же среде на другое расстояние Ь2. Согласно (4.2.4), результирующее матричное соотношение можно записать в виде:
|
|
||
|
|||
Используя хорошо известные правила перемножения матриц, легко пока*? зать, что произведение этих двух квадратных матриц дает следующую пол*' ную матрицу:
1 (Ь1+Ь2)/п
О 1
(4.2.13)
Этот расчет подтверждает очевидный вывод, что результирующее распро-; странение в свободном пространстве эквивалентно такому распространении*: на суммарное расстояние Ь = Ьх+ Ь2.
|
(4.2.14) |
![]() В качестве менее тривиального и более полезного примера рассмотрим распространение на расстояние Ь в свободном пространстве среды с показав телем преломления п = 1, за которым следует отражение от зеркала с радиу1< сом кривизны Я. Согласно (4.2.4), (4.2.7) и (4.2.11), полная АВСХ)-матрицц задается соотношением *
В качестве менее тривиального и более полезного примера рассмотрим распространение на расстояние Ь в свободном пространстве среды с показав телем преломления п = 1, за которым следует отражение от зеркала с радиу1< сом кривизны Я. Согласно (4.2.4), (4.2.7) и (4.2.11), полная АВСХ)-матрицц задается соотношением *
|
А В |
1 0 |
1 Ь |
1 Ь |
||
|
С Б |
-(2/Д) 1 |
0 1 |
-(2/К) 1-(2 Ь/Щ |
Отметим, что определители матриц (4.2.13) и (4.2.14) равны 1, и этот результат оказывается справедливым для любой произвольной последовательности оптических элементов, поскольку определитель произведения матриц равен произведению их определителей.
Обратимся теперь к вопросу о нахождении элементов А', В', С', П лучевой матрицы при распространении луча через оптическую систему в обратном направлении в зависимости от заданнных матричных элементов А, В, С, О для распространения в прямом направлении. Обращаясь к рис. 4.1, видим, что если взять - г2 в качестве вектора на входе, т. е. если поменять направлю
Ниє вектора г2 на противоположное, то вектор ~гх должен быть вектором на выходе. Для обратного распространения будем использовать то же соглашение о знаках, что использовалось для отражения луча от сферического зеркала (рис. 4.2в), а именно: 1) ось г направлена в противоположную сторону, тогда как ось г остается неизменной; 2) угол между вектором г и осью г положителен, если вектор г нужно вращать против часовой стрелки, чтобы направить его вдоль оси г. При этих соглашениях видно, что вектора - Гі и - г2 определяются соответственно координатами (гІ9-г{) и (г2,-г2). Тогда следует записать:
|
П |
А В' |
Г.2 |
|
|
~г{ |
С' I)' |
-Гг |
|
(4.2.15) |
![]() Из (4.2.15) можно найти г2 и г2 в зависимости от гх и г/. Поскольку определитель А'В'С'£>'-матрицы также равен 1, получаем:
Из (4.2.15) можно найти г2 и г2 в зависимости от гх и г/. Поскольку определитель А'В'С'£>'-матрицы также равен 1, получаем:
|
|
||
|
(4.2.17) |
![]() Сравнение (4.2.16) с (4.2.1) показывает, что А' = £>, В' = Б, С' = С, а £>' = А, так что результирующая А'Б'С'1)'-матрица равна
Сравнение (4.2.16) с (4.2.1) показывает, что А' = £>, В' = Б, С' = С, а £>' = А, так что результирующая А'Б'С'1)'-матрица равна
|
А' |
В' |
I) |
В |
|
|
С' |
С |
А |
Таким образом, соотношение (4.2.17) показывает, что матрица для распространения в обратном направлении получается из матрицы для распространения в прямом направлении просто перестановкой матричных элементов А и И.
|
[ Г21 |
|||||
|
Р1^^ |
Оптический Элемент |
|
Рис. 4.4 Распространение сферической волны, испущенной из точки Р19 через обобщенный оптический элемент, характеризуемый данной АВС£>-матрицей |
Матричное представление пригодно не только для описания поведения луча при прохождении им оптической системы, но может быть также использовано для описания распространения сферической волны. Действительно, рассмотрим сферическую волну, исходящую из точки Рх на рис. 4.4 и распространяющуюся вдоль положительного направления оси 2. После прохождения оптического элемента, характеризуемого данной АВС1)-матрицей, такая волна обычно преобразуется в другую сферическую волну, с центром в точке Р2.
Рассмотрим теперь два сопряженных луча гг и г2 этих двух волн, т. е. таких, что оптический элемент переводит падающий (или входящий) луч гх В ВЫХОДЯЩИЙ луч г2. Радиусы кривизны и Я2 фронтов двух волн в плоскости на выходе 2Х и плоскости на выходе г2 оптического элемента нетрудно получить в виде:
|
(4.2.18а) (4.2.186) |
![]()
|
159 |
![]() Яі =П/г{, - Й2 =Г2/Г2'-
Яі =П/г{, - Й2 =Г2/Г2'-
ВА 4. РАСПРОСТРАНЕНИЕ ЛУЧЕЙ И ВОЛН В ОПТИЧЕСКИХ СРЕДАХ
Отметим, что в (4.2.18) использовано следую соглашение о знаках: величина Л положительа если центр кривизны находится слева от волн; вого фронта. Из соотношений (4.2.1) и (4.2.18) получаем:
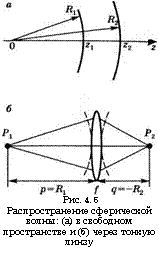
|
Рис. 4.5 Распространение сферической волны: (а) в свободном пространстве и (б) через тонкую линзу |
|
(4.2.19) |
![]() + В СИ + 2)
+ В СИ + 2)
Соотношение (4.2.19) является очень важным результатом, поскольку оно непосредственно связывает радиусы кривизны Н2 и ^ волновых фронтов соответственно на выходе и на входе данного оптического элемента через элементы описывающей его АВС1)-матрицы.
В качестве первого простейшего примера использования этого результата рассмотрим распространение сферической волны в свободном пространстве между точками с координатами и г2 на рис. 4.5а. Из (4.2.4) при п=1и1 = г2-21,а также (4.2.19) получаем: #2 = + (%2 ~ гг)у что> конечно, является очевидным результатом. Рас
Смотрим далее распространение сферической волны через тонкую линзу (рис. 4.5б). Из (4.2.6) и (4.2.19) получаем:
(4.2.20)
Что просто соответствует известному закону геометрической оптики:
Хотя оба примера на рис. 4.5 являются достаточно простыми применениями соотношения (4.2.19), его полезность можно оценить при описании более сложных оптических систем, составленных, например, из последовательности линз, расположенных на некотором расстоянии друг от друга. В этом случае полная АВСБ-матрица определяется произведением матриц для каждого оптического компонента, а радиус кривизны фронта волны на выходе легко определяется с помощью соотношения (4.2.19).