ОПИСАНИЕ С ПОМОЩЬЮ ВОЛНОВОЙ ОПТИКИ
До сих пор рассуждения проводились в приближении геометрической оптики. Для того чтобы получить более реалистичное описание мод в неустойчивом резонаторе, необходимо применять методы волновой оптики, т. е. использовать интегральное уравнение (5.2.5), которое выводится из уравнения дифракции Гюйгенса-Френеля (5.2.1). При этом для неустойчивых резонаторов важным обстоятельством является ограниченность размера апертуры зеркала на выходе, поскольку излучение должно выходить из резонатора вокруг этого зеркала. Следовательно, функция распространения К, которую следует подставить в (5.2.5), в принципе может быть получена точно таким же
методом, который был применен в разделе 5.5.2 для устойчивого резонатора. После этого интегральное уравнение может быть решено с помощью итерационной процедуры, аналогичной процедуре Фокса-Ли, которая была рассмотрена все в том же разделе 5.5.2. Детально обсуждать эти расчеты здесь не будем, а ограничимся только перечислением нескольких существенных результатов и комментариями к ним.
Первый важный результат заключается в следующем: описание с применением методов волновой оптики показывает, что собственные решения уравнения (5.2.5), т. е. такие профили напряженности электрического поля, которые воспроизводят себя после одного обхода резонатора, действительно существуют и в неустойчивых резонаторах. Для того чтобы продемонстрировать это немного более подробно, ограничимся рассмотрением одностороннего неустойчивого конфокального резонатора и определим эквивалентное число Френеля как Иед =[(М-1)/2](а|/ІА) для положительного типа и = [(М + 1)/2](а| /Ьк) для отрицательного типа, где 2а2 — диаметр
Зеркала на выходе. Характерный пример рассчитанного радиального профиля интенсивности, который воспроизводится после одного обхода, показан на рис. 5.19. Расчет относится к конфокальному резонатору положительного типа с М = 2,5 и Мед = 0,6, а профиль интенсивности, соответствует полю распространяющегося вправо пучка внутри резонатора непосредственно перед зеркалом 2 (рис. 5.18б). Профиль интенсивности на рис. 5.19 показан в зависимости от поперечной координаты х (или у)9 нормированной на радиус ах зеркала 1. При этом предполагается, что выход излучения в одном направлении обеспечивается выполнением соотношения а1 = 2,5а2. Следовательно, вертикальные линии на рисунке, проведенные при (х/ах) = ±0,4, показывают края зеркала 2 на выходе.
Исходя из рис. 5.19 можно отметить особый смысл изображенного на нем самовоспроизводящегося при одном обходе неустойчивого резонатора профиля интенсивности. Распространяющаяся влево сферическая волна, фактически отраженная от зеркала 2 (см. рис. 5.186), образована только теми участками показанного на рис. 5.19 профиля интенсивности, координаты которых удовлетворяют условию -0,4 ^ (х/ах) ^ 0,4. Действительно, остальная часть падающего на зеркало 2 излучения проходит вокруг него, образуя пучок на выходе из резонатора. Излучение, оставшееся в резонаторе, в результате совместного влияния сферической расходимости и дифракции пучка после одного обхода резонатора снова будет иметь полный профиль интенсивности, показанный на рис. 5.19. Амплитуда профиля пучка после одного обхода будет меньше исходной из-за потери той части излучения, что вышла из резонатора мимо зеркала 2. Следует также отметить, что профиль на рис. 5.19 заметно отличается от профиля для волны с предполагавшейся постоянной при описании в рамках геометрической оптики амплитудой; это различие обусловлено дифракцией волны в резонаторе, и прежде всего — на краях зеркала 2. Действительно, из рис. 5.19 видно, что если рассматривать координату х как расстояние по радиусу от центра зеркала 2, то в поперечном сечении пучка можно отметить наличие нескольких колец, возникающих в результате дифракции на краях зеркала. Несмотря на существенное
Характерный пример рассчитанного методами волновой оптики поперечного профиля интенсивности в моде неустойчивого резонатора (из [12], с разрешения)
Рис. 5.20
Поперечные профили интенсивности трех мод низшего порядка в планарном неустойчивом резонаторе с М = 2,5 и Аґ„ = 0,6 (из Г10], с разрешения)
Различие профилей интенсивности, предсказанных в приближениях волновой или геометрической оптики, изменения фазы оказываются на удивление одинаковыми при обоих способах описания. Действительно, волновой фронт близок к сферическому, с радиусом кривизны, практически равным величине, полученной в приближении геометрической оптики (т. е. в рассматриваемом случае, непосредственно перед зеркалом 2, этот фронт является плоским).
Вторым существенным результатом описания неустойчивых резонаторов с использованием методов волновой оптики является то, что для них, так же как и для устойчивых резонаторов, существуют отличающиеся друг от друга поперечные моды, т. е. специфические самовоспроизводящиеся пространственные распределения напряженности электрического поля. Обычно эти моды отличаются расположением и интенсивностью дифракционных колец. Пример трех таких мод в конфокальном неустойчивом резонаторе положительного типа показан на рис. 5.20. В отличие от устойчивых резонаторов, в данном случае невозможно провести четкое различие, исходя из вида этих распределений, между модой низшего и модами более высоких порядков. Отметим, что мода, обозначенная на рисунке как I = 0, соответствует распределению амплитуды напряженности поля, более сконцентрированному вокруг оси пучка. Таким образом, в данном случае эта мода имеет наименьшие потери, т. е. является «основной» модой.
Третий характерный результат можно найти, если варьировать эквивалентное число Френеля, т. е. как-то изменять величины параметров М, а2 или Ь. Фактически при каждом целом значении эквивалентного числа Френеля модой низшего порядка, т. е. модой с наименьшими потерями, становятся различные определенные моды резонатора. Это утверждение можно понять с помощью рис. 5.21, на котором приведена зависимость модуля собственного значения а отЫед для трех мод, показанных на рис. 5.20. Действительно,
|
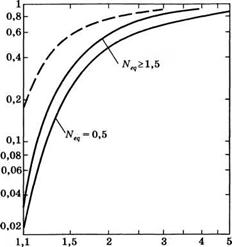
М Рис. 5.22 Потери за счет выхода излучения из неустойчивого резонатора в зависимости от коэффициента увеличения М (из [13], с разрешения) |
|
Рис. 5.21 Характерный пример осциллирующей зависимости модуля собственного значения а от эквивалентного числа Френеля Мед для трех соседних мод на рис. 5.20 |
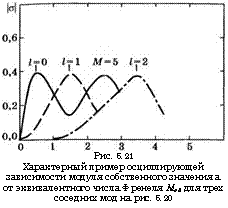 Заметим, что поскольку у = 1 — |а|2, мода с / = 1 становится модой низшего порядка, когда Ыед принимает значения больше 1 (и меньше 2). Причина этого заключается в том, что по мере увеличения Ыед, начиная, например, с = 0,6
Заметим, что поскольку у = 1 — |а|2, мода с / = 1 становится модой низшего порядка, когда Ыед принимает значения больше 1 (и меньше 2). Причина этого заключается в том, что по мере увеличения Ыед, начиная, например, с = 0,6
На рис. 5.20, пучок моды с / = 1 сжимается к оси, а моды с / = 0 — расширяется, так что при Ыед = 1 эти две моды меняются местами с точки зрения величины потерь. Из рис. 5.21 видно также, что при каждом полу целом значении Ыед разница величин потерь для моды низшего порядка и для других мод весьма значительна. Может показаться, что такие значительные различия в потерях для поперечных мод могут быть получены только при этих условиях. Однако отметим, что при тех условиях, когда кривые потерь для двух мод пересекаются, (т. е. при целых значениях Ыед на рис. 5.21), распределения интенсивностей в этих двух модах становятся идентичными. Таким образом, например, при Ыед = 1 существует большая разница в величине потерь для моды с / = 2 и мод с/ = 0и/=1, которые с точки зрения поперечного профиля пучка можно рассматривать как эффективно являющиеся одной и той же модой.[27] В заключение отметим, что для неустойчивых резонаторов всегда характерны значительные различия в потерях для поперечных мод, которые, пожалуй, наиболее сильны при полу целых значениях Мед.
Можно также указать на то, что из расчета с использованием методов волновой оптики при полуцелых значениях Иед величина потерь для моды
Низшего порядка получается значительно меньше той, которую можно предсказать на основе геометрической оптики. Это хорошо видно из рис. 5.22, на котором показаны потери у за счет выхода излучения из неустойчивого резонатора в зависимости от коэффициента увеличения за обход М. Сплошными линиями на рисунке (которые соответствуют последовательным полуцелым значениям Иед) показаны зависимости, полученные с помощью волновой оптики, а пунктирная линия соответствует выражению (5.6.5), полученному из соображений геометрической оптики. Видно, что в любом случае потери для моды низшего порядка меньше величины, предсказываемой с использованием геометрической оптики. Этот результат обусловлен тем фактом, что интенсивность в моде низшего порядка концентрируется вблизи оси пучка (см. рис. 5.20), а не равномерно распределена по его поперечному сечению, как это предполагается в рамках геометрической оптики.