ПРИНЦИПЫ ЛАЗЕРОВ

КРИТЕРИЙ УСТОЙЧИВОСТИ

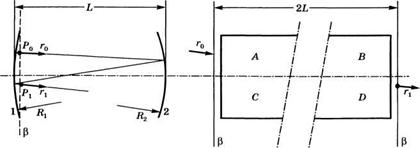
Рассмотрим вначале двухзеркальный резонатор общего вида (рис. 5.6а) и луч, идущий из точки Р0 плоскости Р внутри резонатора, например прямо перед зеркалом 1. Этот луч после отражения от зеркал 2 и 1 пересечет плос­кость Р в некоторой точке Рг. Если обозначить через г0 и гг поперечные коор­динаты точек Р0 и Рг относительно оси резонатора, а через г0' и г{ — углы, которые соответствующие лучи образуют с этой осью, то в соответствии с

(4.2.2) можно записать:

Гу А В г0

Г{ С £> Го’ (5.4.1)

Где АВС2)-матрица отвечает одному обходу резонатора. Луч, выходящий из точки Рі(гі, гі'), пересечет после одного обхода плоскость р в точке Рг(г2> г2.) с обобщенными координатами

(5.4.2)

Таким образом, после п обходов соответствующая точка Рп (гп, г'п) будет иметь координаты

Для того чтобы резонатор был устойчивым, требуется, чтобы для любой на* чальной точки (г0,Го) координаты точки (гп, г^) оставались конечными при увеличении п. Это означает, что элементы матрицы

А Вп С И

Также должны оставаться конечными по мере роста п.

Предшествующие рассуждения можно легко распространить на обобщен­ный резонатор, в котором преобразование луча при одном обходе описывает­ся некоторой АВС1)-матрицей, например на резонатор из двух зеркал, содер­жащий другие оптические элементы, такие как линзы, телескопы и т. д. (см. рис. 5.66). В этом случае снова требуется, чтобы элементы АВС£>-матри- цы в п-ой степени оставались конечными по мере роста п.

Для обоих резонаторов, изображенных на рис. 5.6, луч исходит из плос­кости Р и приходит на нее же, что означает неизменность показателя пре­ломления для обоих лучей — начального г0 и конечного гх. Отсюда следует, что определитель матрицы, (АО-ВС), равен 1. В этом случае теорема матрич­ной алгебры [2], иногда называемая теоремой Сильвестра, гласит, что если угол 0 определен в соответствии с соотношением

Сов0 = (А 4-1))/2, (5.4.4)

То справедливо равенство

Соотношение (5.4.5) показывает, что матричные элементы п-ой степени мат­рицы не возрастают до бесконечности, если величина 0 является действитель­ной. На самом деле, если бы величина 0 была комплексной, т. е. имела бы вид

0 = а 4- ib, то члены, пропорциональные, например, sinn0 в (5.4.5), могли бы быть представлены как sin п0 = [ехр(уя0) 4- ехр(-уя0)]/2у = [exp (jna - пЪ) -

- exp (-jna 4- nb)]/2j. Тогда величина sin я0 содержала бы вклад, который мог бы экспоненциально возрастать при увеличении п, например [exp (-jna + 4- nb)]/2j при b > 0, так что элементы п-ой степени матрицы стремились бы при этом к бесконечности по мере роста п. Таким образом, для устойчивости резонатора потребуем, чтобы величина 0 была действительной; согласно (5.4.4), это означает, что должно выполняться условие

-1<(^)<, (5.4.6)

Неравенство (5.4.6) устанавливает критерий устойчивости для обобщен­ного резонатора на рис. 5.66. В случае двухзеркального резонатора, изобра­женного на рис. 5.6а, можно сделать следующий шаг, записав АБС£)-матри - цу в явном виде. Напомним, что полную матрицу для системы можно полу­чить как произведение матриц отдельных оптических элементов, которые пересекает пучок, при этом матрицы должны быть расположены в очередно­сти, обратной той, в которой пучок проходит сквозь соответствующие эле­
менты. Таким образом, в рассматриваемом случае АВСР-матрица задается упорядоченным произведением следующих четырех матриц: отражение от зеркала 1, распространение в свободном пространстве от зеркала 2 к зерка­лу 1, отражение от зеркала 2, распространение в свободном пространстве от зеркала 1 к зеркалу 2. Используя табл. 4.1, получим:

Матричное произведение (5.4.7) дает

А + Б

2 Ь 21?

2Ь

2 Й! й2 + Соотношение (5.4.8) можно легко привести к виду:

А + Б

(5.4.9)

Удобно теперь ввести две безразмерные характеристики резонатора, кото­рые называют g1- и £2-параметрами резонатора и определяют как

Ё1 = 1 -(Ь/ДО, (5.4.10а)

£2=1 -(£/Я2). (5.4.106)

Используя эти параметры, критерий устойчивости (5.4.6), выраженный в виде (5.4.9), легко записать в очень простой форме:

0<ё1ё2<1. (5.4.11)

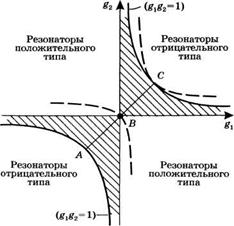
Критерий устойчивости (5.4.11) удобно изобразить графически в плоско­сти #2 (рис. 5.7). Для этого на рис. 5.7 представлены две ветви гиперболы,

Описываемой уравнением ёг • #2 = 1 (сплошные линии). Поскольку другое гра­ничное условие в (5.4.11), а именно £1 ■ £2 = 0, требует, чтобы либо = 0, либо §2 = то области устойчивости в плоскости §2 отвечает заштрихованная

Часть рисунка. Особенно важный класс двухзеркальных резонаторов пред­ставлен точками отрезка прямой АС, образующего угол 45° с осями gl и£2. Этот отрезок соответствует резонаторам с зеркалами одинаковой кривизны (симметричным резонаторам). В качестве конкретных примеров таких сим­метричных резонаторов можно указать те из них, которые отвечают пока­занным на рисунке точкам А, Б и С и являются соответственно концентриче­скими, конфокальными и плоскими резонаторами.

Следует отметить, что резонаторы указанных трех типов, отвечающие точкам А, Б и С, и, вообще говоря, любые резонаторы, параметры которых удовлетворяют соотношениям £1 • = О или ' &2 = 1» находятся на грани­

Це, разделяющей области устойчивости и неустойчивости. В таких резонато­рах только некоторые из лучей, например лучи, перпендикулярные плоским зеркалам на рис. 5.1а, не расходятся по мере распространения. Поэтому го­ворят также, что эти резонаторы являются минимально устойчивыми. Усло­вия • £2 = 0 или ёх • ё2 = 1 соответствуют, таким образом, минимально ус­тойчивым ситуациям.