ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ВЛИЯНИЕ ОТНОСИТЕЛЬНОЙ ГЛУБИНЫ КОНЦЕНТРАТОРА
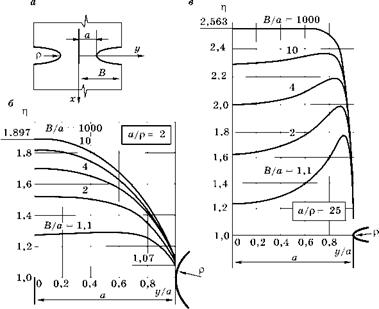
Распределение жесткости напряженного состояния в минимальном сечении (х = 0) пластины с двусторонней гиперболической выточкой приведено на рис. 3.24.
В левой части этого рисунка показаны графики для концентратора сравнительно малой остроты: а/р = 2. Видно, что если такой концентратор имеет глубину порядка 10% от минимального сечения (В/а = 1,1), то жесткость напряженного состояния не превышает 1,3; т. е. максимальные нормальные напряжения не могут превышать предел текучести более чем на 30%.
Чтобы получить жесткость напряженного состояния ^ = 1,8, нужно изготовить образец, в котором глубина надрезов в 10 раз превышает размер минимального сечения, т. е. глубина дефекта должна уменьшать сечение пластины на 90%.
Естественно, что в нормальных деталях машин или конструкций такая конфигурация практически не встречается. Она может возникнуть в случае, когда у многопроходного стыкового шва с двусторонней разделкой выполнены только корневые проходы. Дальнейшее увеличение глубины надреза до B/t = 100 повышает максимальную жесткость напряженного состояния совсем немного (до ^ = 1,897).
|
Рис. 3.24 Распределение жесткости напряженного состояния по минимальному сечению у двустороннего гиперболического надреза при разной его относительной глубине B/а при растяжении |
В правой части рис. 3.24 показаны те же зависимости, но для сравнительно острых надрезов (а/р = 25). Видно, что в этом случае при всех имеющих практическое значение глубинах надрезов (B/t < 10) максимум ^ сдвигается по сравнению с предыдущим графиком от центра сечения к корню надреза. Но даже при В/t = 10, ^ < 2,4 только при неправдоподобно глубоких надрезах (B/t = 1000) жесткость напряженного состояния приближается к своему максимальному значению для плоской деформации (^ = 2,566), показанному на рис. 3.23 при а = 1 и m = 0.
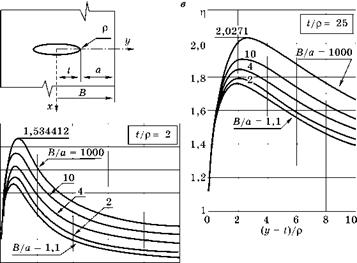
На рис. 3.25 приведены такие же графики для минимального сечения пластины у внутреннего эллиптического отверстия.
Заметим, что в отличие от предыдущего рисунка по оси ординат отложена не координата у, а расстояние рассматриваемой точки от вершины концентратора, отнесенное к его минимальному радиусу. Кроме того, параметрр, входящий в формулы (3.20) для вычисления напряжений у этого концентратора, определен только для пластины бесконечной ширины. Поэтому, в случае пластины ограниченной ширины для нахождения среднего напряжения р0
|
|
|
10 |
|
Рис. 3.25 Распределение жесткости напряженного состояния в минимальном сечении пластины с эллиптическим отверстием |
|
а |
|
б 1,6 л 1,4 1,2 1,0 |
|
(у - О/р |
в сечениях, удаленных от концентратора, которое входит в формулу (3.28), необходимо прибегнуть к интегрированию:
|
B Ро p |
Ро = B' J(y)dy, (3.56),
|
(B2/t2 + 2t / р-2) yjB2/t2 +р/t-1 ' I P |
после которого получим:
P-3 ,^B2/12 *P/1-1*^^1 J-f
Следует заметить, что увеличение B/t, которое входит в формулу для p0, соответствует уменьшению относительной глубины концентратора. Поэтому при построении кривых отношение B/t, входящее в последнюю формулу, пересчитывалось в соответствии со схемой рис. 3.25 на отношение B/a = (B/t)/(B/t - 1).
В левой части рис. 3.25 показана зависимость ^ от относительной глубины концентратора. На правом графике показано влияние относительной остроты концентратора.
Видно, что в случае мелкого надреза максимальная жесткость напряженного состояния достигается на расстоянии 1-2 радиусов от дна надреза. Правда, для надрезов значительно большей остроты это расстояние может доходить и до 10р.
Как и для внешних надрезов, ^ увеличивается с увеличением остроты t/р и относительной глубины В/а надреза. Но уровень максимальных значений жесткости несколько ниже, чем у двусторонних выточек. Даже при В/а = 1000 жесткость напряженного состояния на этих графиках не достигает своего максимального значения 2,566, получаемого при плоской деформации.