ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ВЛИЯНИЕ ЧИСЛА ЦИКЛОВ НА РАЗРУШАЮЩУЮ НАГРУЗКУ
В области многоцикловой усталости зависимость прочности от числа циклов устанавливают по экспериментальным результатам. Для этого испытывают одинаковые образцы при разных уровнях максимальных напряжений amax и отмечают число циклов Nf, при
|
Таблица 6.9 Результаты испытаний сварных пластин стали 10Г2С1 сечением 80x26 мм со стыковым швом. Растяжение г = 0
|
котором происходит полное разрушение образца. Так как построение такой кривой требует много времени, обычно ее экспериментально получают только для симметричного цикла (г = -1), который в лаборатории легко воспроизводится на быстроходных (до 6000 циклов в минуту) испытательных машинах, нагружающих вращающийся образец чистым изгибом при его вращении. Большие сварные образцы испытывают на больших пульсаторах с максимальным усилием от 300 до нескольких тысяч тонн и частотой около 300 циклов в минуту. При этом часто образец не удается нагрузить сжатием. Он не совсем равный, при сжатии изгибается, может терять устойчивость. В этом случае при испытаниях применяют пульсирующий отнулевой цикл растяжения с характеристикой г * 0.
Для определения выносливости листов стали или сварных соединений испытывают серию из 10-20 одинаковых образцов. Первый образец испытывают при amax несколько ниже предела текучести. Определяют число циклов, при котором в нем возникает трещина усталости. При испытаниях следующего образца несколько снижают нагрузку и вновь определяют число циклов до разрушения. Испытания прекращают, когда несколько образцов выдерживают около 2 млн циклов. Нетрудно подсчитать, что для того, чтобы получить 2 млн циклов, один сварной образец на пульсаторе (при 300 циклах в минуту) нужно испытывать непрерывно в те
чение около 5 суток. Испытания образцов у предела усталости стоят очень дорого.
Результаты испытаний представляют в виде табл. 6.95.
При этих испытаниях для каждого образца фиксировали три значения числа циклов: при первом появлении усталостной трещины, при ее росте до 2-3 мм (это значение считалось концом стадии зарождения усталостного разрушения) и по моменту окончательного разлома образца.
При математической обработке таких результатов обычно пользуются линейной регрессией. Советские исследователи (В. И. Тру - фяков в инстиуте электросварки им. Е. О. Патона, И. В. Кудрявцев в ЦНИИТМАШе и др.) обычно пользовались регрессией в полулогарифмических координатах (а - log(N)). В этом случае результаты представлены формулой
|
|
(6.163)
где ar, N — предел усталости, определенный для заданной при испытаниях характеристики цикла r и числе циклов до разрушения N при вероятности разрушения Р = 50%; аЕ — экспериментальное значение предела усталости при максимальном в эксперименте числе циклов NE = 2106 и заданной характеристике цикла r; k — тангенс угла наклона прямой; sN1 — среднеквадратичное (нормальное) отклонение экспериментальных точек от прямой линейной регрессии с P = 50%. Оно имеет размерность напряжений, что удобно при интерпретации результатов.
Формула написана так, чтобы под знаком логарифма была безразмерная величина. Размерность под знаком логарифма абсурдна.
Европейские и американские исследователи представляют такие результаты в двойных логарифмических координатах log(a) - log(N). В этом случае результаты экспериментов описываются
|
или |
формулой
|
|
|
|
(6.164)
Зависимость (6.164) от N похожа на формулу (6.157) для малоцикловой усталости. Она линейна в двойных логарифмических координатах. Здесь среднеквадратичное отклонение sN2 не имеет
5 Данные таблицы из: Труфяков, В. И. Усталость сварных соединений. — Киев : Наукова думка, 1973.
|
|
|
Коорди наты |
No |
N |
Na |
2s» |
от |
Уравнение для зарождения трещины |
|
Полуло- гариф- мические |
7,5-105 |
1,16-106 |
2,4-106 |
2,51 |
12,8 |
0-1, N — 81,6 — - 11,3 - log(N)± 1,25 |
|
Лога рифми- ческие |
1,1-106 |
1,59-106 |
3,2-106 |
0,052 |
12,7 |
°-1, N 12,7 С N Л-0_247 I N 1 -|0±0.П26 11,59-106 J |
|
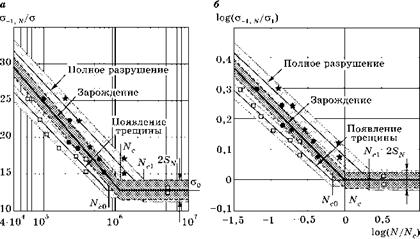
Рис. 6.74 Результаты обработки данных табл. 6.9 в полулогарифмических (а) и в двойных логарифмических координатах (б) |
размерности. Можно заметить, что sN2 = log(n), где n — множитель, аналогичный коэффициенту запаса прочности, на который нужно умножить или разделить ar, N, чтобы получить границы полосы разброса экспериментальных точек.
Чтобы сравнить эффективность выбора той или иной системы координат, на рис. 6.74 показаны результаты обработки данных из табл. 6.9.
Наклонные сплошные прямые представляют собой линии средних значений ст0, N при вероятности разрушения Pf = 50%. На каждом графике нанесены три таких линии. Первая проведена по светлым квадратным точкам, показывающим число циклов, при котором впервые обнаружено появление усталостной трещины. Вторая жирная линия проведена по черным круглым точкам, которые соответствуют росту усталостной трещины до 2-3 мм. Эта величина трещины обычно считается критерием завершения стадии зарождения усталостного разрушения. Третья линия проведена по черным звездочкам, которые обозначают полное разрушение образца. Для каждой линии пунктиром показаны границы полос стандартных отклонений шириной 2sN, которые залиты точками разной плотности.
Предел усталости определен приближенно по двум образцам, которые не разрушились при 2 млн циклов. Критическое значение числа циклов Nc определено по точке пересечения наклонной прямой с горизонтальной линией предела усталости.
Считается, что ширина полосы разброса экспериментальных точек (2sn) не зависит от числа циклов. Поэтому ширина полосы разброса предела усталости может быть определена в результате линейной регрессии координат экспериментальных точек на наклонной части графика.
Среднее значение предела усталости показано на графиках жирной горизонтальной прямой. Ниже, в таблице, даны три значения критического числа циклов, определенные по трем критериям: Nc0 — появление зародыша трещины; Nc — завершение стадии зарождения трещины; Nc1 — полное разрушение образца. Значения этих параметров зависят от системы координат, в которых производится обработка.
Cравнивая числа циклов для точек перегиба линий этих графиков, можно получить представление о длительности каждой стадии разрушения при испытаниях стыкового сварного соединения. Например, предел усталости по критерию появления трещины при обработке в двойных логарифмических координатах достигается примерно после 1 млн циклов. Стадия роста малой трещины до критического размера (2-3 мм) требует около 0,6 млн циклов. Стадия распространения корректной усталостной трещины до полного разрушения длится около Nc1 - Nc = 3,2 - 1,6 = 1,6 млн циклов, т. е. столько же, сколько циклов требуется для зарождения трещины и роста ее до критической величины 2-3 мм. При обработке результатов в полулогарифмических координатах (рис. 6.74а) эти критические значения чисел циклов оказываются существенно меньше.
Сравним эти два способа обработки по ширине полосы разброса при Nc. При обработке в полулогарифмических координатах эта ширина составляет 2sN = 2,51 кГ/мм2. При обработке в двойных логарифмических координатах ширину полосы можно вычислить по формуле
Аа0 = а0 • (10sn -10-sn ) = 12,909 • (10°,°26 -10-°,°26) = 1,547 Кг/мм2.
Это меньше, чем при обработке в полулогарифмических координатах. Но с уменьшением числа циклов ширина полосы стандартных отклонений в двойных логарифмических координатах увеличивается. Например, при ст0, N = 26 кг/мм2 ширина полосы будет в два раза больше и составит около 3 кг/мм2, что больше, чем при обработке в полулогарифмических координатах.
Таким образом, сравнивая два способа обработки результатов эксперимента, приведенных в табл. 6.9, нельзя с уверенностью сказать, какая система координат заведомо лучше.
|
ст. |
В расчетных нормах для зависимости предела усталости от числа циклов обычно используются приведенные графики (рис. 6.746) при симметричном цикле. На этих графиках по оси ординат откладывается значение предела усталости при ограниченном числе циклов ст_!, N, равное амплитудному значению предела усталости (ста, N), отнесенное к экспериментальному значению предела усталости стЕ, полученному при стандартном для рассматриваемых норм числе циклов Ne. Обозначим это отношение, как в СНиП, буквой а:
1, N
а" СТЕ ■ (6.165)
Зная значение а и экспериментальное значение предела усталости стЕ, предел усталости при заданном числе циклов можно определить по формуле
ст-1, N = а • стЕ. (6.166)
До 1960 годов считалось, что физический предел усталости сварных соединений конструкционной стали достигается при 2 млн циклов. Поэтому принималось NE = 2106 и стЕ = ст-1, т. е. полагали, что стЕравно физическому пределу усталости. В последующие годы экспериментально установили, что физический предел усталости для разных сталей и разных типов сварных соединений достигается в широком диапазоне чисел циклов. Например, в монографии В. И. Труфякова приведена таблица, включающая результаты испытаний 45 серий сварных образцов различных конструкций из 15 марок сталей. Из этой таблицы следует, что точка перелома может находиться в интервале от 1,5 до 4 млн циклов. Вероятно, чтобы не потерять ранее накопленные экспериментальные результаты, в европейских и американских нормах оставили NE = 2106. Тогда стЕ можно назвать экспериментальным (условным) значением предела усталости при r = -1 и числе циклов N = NE = 2106.
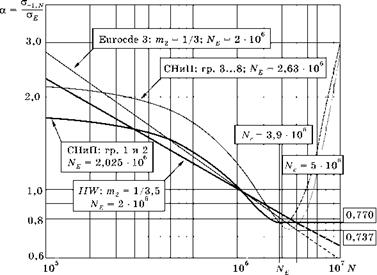
На рис. 6.75 показаны 4 кривые зависимости коэффициента а от числа циклов:
|
Рис. 6.75 Обобщенные кривые зависимости ограниченного предела усталости от числа циклов по трем нормативным документам |
IIW — линия для сварных соединений конструкционных сталей по рекомендациям Международного института сварки (International Institute of Welding), 1990 г.;
Eurocde 3 — линия по Европейскому стандарту для сварных соединений конструкционных сталей, 1992 г.
В этих нормах влияние числа циклов на коэффициент а описывается степенной зависимостью. В двойных логарифмических координатах функции a(N) представлены прямыми линиями с угловыми коэффициентами т2 = 1/3,5 и т2 = 1/3:
Ч N Г - <6лв7>
Кроме того, на рисунке приведены две кривые, построенные по СНиП II-23-81*), 1990 г., которые описываются полиномами второй степени от числа циклов N:
■ для 1 и 2 групп соединений:
а( N) = 1,75 - 0,5 • (N-) + 0,064 •( N ^ (6.168)
■ для 3-8 групп соединений:
a(N) - 2,2 - О.64 •( N)+ 0,07'(N J".
Число циклов Ne, при котором определяется экспериментальный предел усталости аЕ и а = 1,0, у этих линий отличается от европейских норм. Для сварных соединений групп 1 и 2 с малой концентрацией оно близко к европейским (Ne = 2,025 106), но для сварных соединений групп 3-8 оно заметно больше (Ne = 2,63 106).
По всем приведенным нормам число циклов Nc, при превышении которого назначается физический предел усталости, и прочность не зависит от числа циклов, существенно превышает Ne. По строительным нормам и правилам для любых групп сварных соединений Nc = 3,9106, а отношение физического предела усталости к его экспериментальному значению для всех групп сварных соединений а = 0,77. По Eurocode 3 и рекомендациям IIW физический предел усталости достигается при Nc = 5106 циклов. Как видно из рисунка, относительное значение предела усталости по рекомендациям IIW при этом числе циклов равно а = 0,77, что совпадает с нормами СНиП. Но по Eurocode 3 относительное значение физического предела усталости оказывается меньшим и равно 0,737 от экспериментального значения аЕ. Это связано с тем, что наклон прямой по Eurocode 3 больше.
Обычно, если наклонная прямая в двойных логарифмических координатах представляется несколькими отрезками прямой, то наклон этих отрезков уменьшается с ростом числа циклов.
|
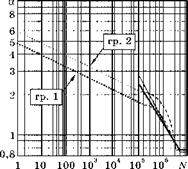
Рис. 6.76 Зависимость коэффициента а от числа циклов в более широком диапазоне |
Коренное отличие формы двух нормативных кривых для расчетов на усталость рис. 6.75, вычисленных по СНиП, от нормативной наклонной прямой линии, вычисленной по нормам Международного института сварки (IIW), вызывает удивление. Такие же наклонные нормативные прямые линии используются в в расчетах на усталость в европейском стандарте Eurocde 3 и американском стандарте ASTM.
Возможно, уменьшение наклона линий а по СНиП с уменьшением числа циклов на рис. 6.75 связано с переходом к малоцикловой усталости. Чтобы прояснить этот вопрос, на рис. 6.76 все кривые рис. 6.75 построены в более мелком масштабе, а в левой части графика нанесены две прямые линии малоцикловой усталости. Для этого ординаты прямой линии рис. 6.69 были поделены на пре
делы усталости аЕ сварных соединении первой и второй группы стали с пределом прочности 540 МПа по табл. 6.8.
|
1 m2 |
Если напряжения цикла меняются во времени, то для определения долговечности можно использовать гипотезу линейного суммирования повреждений. Из формулы (6.164) следует, что число циклов до разрушения при заданном амплитудном напряжении а можно вычислить по формуле
N = ne
Это выражение далее можно подставить в формулы (6.158) и (6.159) для линейного суммирования повреждений при заданном спектре нагрузок, подобно тому, как это было показано для малоцикловой усталости: тогда
1
-f - NN {th (6.169)
а предельное состояние для n ступеней нагружения при ai > ас выразится формулой
XAdi = {N 1 _ JXANi-am =1. (6.170)
i=1 ^ ne 'Qe J i=1
При использовании формулы (6.170) следует учитывать, что она достаточно точно работает, если напряжения каждого последующего цикла равны или больше, чем напряжения в предыдущем цикле. Если это правило нарушается, то после цикла с большими напряжениями при последующих циклах с меньшими напряжениями степень повреждения металла оказывается меньшей, чем это следует по формуле (6.169) для постоянных напряжений. Наблюдается «эффект перегрузки». В этом случае расчеты по гипотезе линейного суммирования повреждений дают заниженное количество циклов и идут в запас надежности. В литературе можно найти результаты исследований, позволяющие уточнить этот расчет.