ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ У КОНЦЕНТРАТОРОВ
Ниже приводятся решения для полей линий скольжения, взятые из книги Л. М. Качанова «Основы теории пластичности». Настоятельно рекомендую читателям использовать ее, если они в своей инженерной деятельности встретятся с подобными задачами.
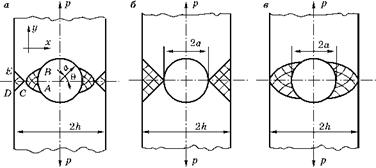
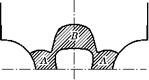
На рис. 3.51 показаны три варианта полей линий скольжения в растянутой полосе, шириной 2h с круглым отверстием радиуса а в центре.
На рис. 3.51а предполагается, что нагрузкаp такова, что условие текучести І! = k выполняется только в пределах дуги AB контура отверстия. К границе, описанной по дуге окружности, должен прилегать участок осесимметричных линий скольжения (рис. 3.49).
Если точка B находится под центральным углом 0В, то угол наклона крайней верхней линии скольжения в точке В равен фв = а = 0В + л/4. В точке С по условию симметрии тху = 0. Ось х является главной осью. Следовательно, линия скольжения должна быть наклонена к этой оси под углом фС = 5л/4.
Приращение угла ф между точкой B и точкой С составит: Аф = фС - фв = 5л/4 - (0B + л/4) = л - 0B. Радиус до точки B можно
|
Рис. 3.51 Три вида полей линий скольжения у кругового отверстия в растянутой полосе |
найти из формул (3.113): ra = a ■ ехр(фа - а) = a ■ ехр(л - 0В), а напряжения в точке С по формулам (3.112) и (3.107) приpa = 0:
|
=°ma +2k-A(p = k + 2k-(л-0в );
|
(3.115)
+k = 2k-(Л-0В +1) = 2k ■ ln [ ra j + 1 .
Так как угол 0В не может быть согласно рисунку больше л/2, ra < a ■ ехр(л/2).
Последнее равенство формул (3.115) справедливо для любой точки оси х в пределах a < r < га. Следовательно, по минимальному сечению эпюру напряжений на этом участке можно представить формулой
|
|
(3.116)
На больших расстояниях от отверстия к прямой вертикальной границе полосы прилегает поле линий скольжения однородного напряженного состояния (рис. 3.51a). В пределах этого участка:
°x =^3 = 0;
|
(3.117) |
=®m = ст3 + k = k;
=®m + k = 2k.
Теперь из условия равновесия можно найти либо величину приложенных средних напряжений p по заданному углу 0В или радиусу га, или по заданной нагрузке определить 0В или га. Запишем условие равновесия:
|
a |
(3.118)
|
|
Второй вариант поля линий скольжения (рис. 3.516) получается из первого, если принять 0В = 0; или ra = a. Тут все минимальное сечение занимает однородное поле напряжений. Соответствующая этому варианту нагрузка:
|
(3.119) |
p ■ h = 2k ■ (h - a).
Наконец, в третьем возможном варианте поля линий скольжения на все минимальное сечение распространяется область логарифмических спиралей rc = h. Разумеется, это возможно только
при h < а ■ ехр(л/2) = 4,81 а. В этом случае выражение (3.118) приобретает вид:
|
|
(3.120)
Сравнивая формулы (3.118)-(3.120), можно сделать вывод, что формула (3.119) дает минимальное значение для внешней нагрузки. Следовательно, прежде будет реализовываться именно второй вариант поля линий скольжения (рис. 3.516). Для того чтобы быть уверенным в этом умозаключении, нужно быть уверенным в том, что, действительно, пересмотрены все возможные конфигурации полей линий скольжения и из них выбран тот вариант, который соответствует наименьшей нагрузке.
Еще одно замечание. В точке С эпюра напряжений ar = ах (рис. 3.51а) имеет скачок. Справа от точки С: ах =2k ■ (л - 0B); слева от точки С: ах = 0. Следовательно, в точке С нарушаются дифференциальные условия равновесия.
Такую неоднозначность результатов вычислений, полученных методом линий скольжения, нужно всегда иметь в виду.
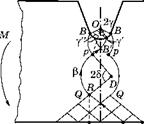
На рис. 3.52 показано поле линий скольжения в растянутой пластине с двусторонними трещинами.
Поле состоит из трех типов сеток.
1. Треугольные области равномерного напряженного состояния OABO, прилегающие к поверхностям трещин. В них всюду:
°х = °1 = 2k;
°y = °3 = 0;
= k.
2. Секторные области центрированных полей OBCO у вершины трещины — в этих областях угол ф изменяется на Лф = л/2. В результате гидростатические напряжения увеличиваются на Лстт = 2k ■ л/2. Тогда на линии OC имеем:
az = ат = k + Лат = (л + 1) ■ k; ау = ^1 = ат + k = (л + 2) ■ k; °x = °3 = ®т - k = л ■ k.
3. Две квадратные области равномерного напряженного состояния OCD — здесь всюду напряжения равны тем, что были вычислены выше для линии OC.
В минимальном сечении нет концентрации напряжений. Жесткость напряженного состояния:
|
|
|
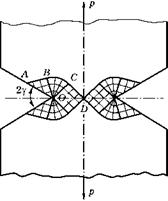
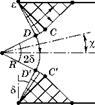
Рис. 3.53 Линии скольжения у двустороннего надреза с углом 2у |
Напомним, что для такой же упругой задачи максимальная жесткость была равна 2,56. Следовательно, при переходе от локальных пластических деформаций к общей текучести жесткость напряженного состояния у двустороннего надреза возрастает.
Влияние угла раскрытия острого надреза позволяет проанализировать поле линий скольжения, представленное на рис. 3.53, где имеются те же три типа областей, что и на предыдущем рисунке.
В областях OABO главные напряжения ^ и а3 те же по величине, что на рис. 3.52. Но их площадки, по сравнению с предыдущим рисунком, повернуты на угол у. Отличие заключается в том, что угол поворота линий скольжения в центрированных областях OBCO уменьшился на у. Следовательно, все напряжения в областях OCD с равномерным напряженным состоянием уменьшаются на 2k ■ у, по сравнению с рис. 3.52:
стг = ат = k + А<зт = (л + 1 - 2у) ■ k; ау = сті = ат + k = (л + 2 - 2у) ■ k;
= °3 = - k = (л - 2у) ■ k.
Жесткость напряженного состояния в минимальном сечении определяется формулой
ст1 _ (л + 2 -2у)
л=-
Если угол у достигнет л/2, то надрезы исчезнут. При этом жесткость напряженного состояния будет равна Л = 2/7э, что связано с наличием плоского деформированного состояния (запрещением деформаций в направлении оси z).
|
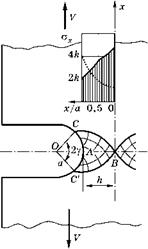
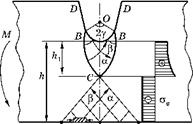
Рис. 3.54 Линии скольжения у двустороннего надреза с радиусом а |
На рис. 3.54 показано поле линий скольжения у двустороннего надреза с конечным радиусом закругления а в случае, когда полуширина минимального сечения h < а ■ ехр(л/2) = 4,81 а.
|
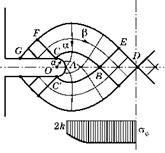
Рис. 3.55 То же, что рис. 3.54, но при большем значении h |
Здесь логарифмические спирали линий скольжения распространяются от поверхности концентратора до центра детали. Вид эпюры напряжений О = оу по минимальному сечению показан в верхней части рисунка. Пунктирной кривой показано распределение напряжений, вычисленное по первой формуле (3.13) для упругого материала и а/р = 1.
Сплошной кривой показано распределение напряжений, вычисленное по формуле (3.116) для стадии общей текучести.
Обратите внимание, как изменился вид эпюры напряжений при переходе от упругой стадии нагружения к общей текучести. В последнем случае максимум напряжений в центре сечения, где оу = 2k ■ [1 + ln(h/a)].
|
Рис. 3.56 Экспериментальное поле пластических деформаций |
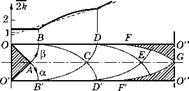
На рис. 3.55 показано поле линий скольжения для таких же надрезов, как на рис. 3.54, но ширина сечения h > а ■ ехр(л/2).
В этом случае поле с логарифмическими спиралями занимает область ACBC’A. Расстояние OB = а ■ ехр(л/2). От точки C, где от = k, до точки B угол ф изменяется на Аф = л/2. Следовательно, в точке В средние напряжения
ътв=k+2k • 2.
Такими они сохраняются до точки D во всей области равномерного напряженного состояния. Напряжения стф = ау = ст1 в центральной части сечения:
|
|
Эпюра этих напряжений в минимальном сечении показана в нижней части рис. 3.55.
Кроме знакомых областей линий скольжения здесь добавлены области CFEBC c простым напряженным состоянием. В этих областях напряжения постоянны при движении вдоль стрелок а и изменяются при движении в направлении стрелок р. Видно, что при пластическом растяжении материал в направлении стрелок р может перетекать от кромок надреза к центральным частям сечения — к области BED. Только в результате такого перетекания материала пластина может увеличивать свою длину.
Но экспериментально это поле может и не быть реализовано. На рис. 3.56 показаны результаты травления продольного сечения предварительно пластически растянутой пластины.
Видно, что заштрихованные контуры зон пластической деформации (A и B) совсем не похожи ни на рис. 3.55, ни на рис. 3.54. Здесь пластическая деформация «обошла» зону с высокой жесткостью напряженного состояния, о которой говорилось при анализе упругого решения для пластин с двусторонними гиперболическими надрезами Нейбера.
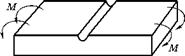
Аналогично можно анализировать и напряженное состояние надрезанных пластин в условиях общего течения при изгибе. Схема такой пластины с односторонним надрезом показана на рис. 3.57.
|
|
|
Рис. 3.57 Схема изгибаемой пластины |
Так производят испытания материалов и сварных соединений. Поэтому приведенный ниже анализ представляет значительный интерес для интерпретации результатов таких испытаний.
На рис. 3.58 показаны два варианта полей для изгибаемой пластины с концентратором.
Согласно левому варианту вращение жестких частей пластины происходит вокруг точки С. Выше этой точки материал растянут и сдвиги идут вдоль логарифмических спиралей семейств а
|
|
|
м. |
|
О” А' А |
|
|
|
A -2k I O' А |
|
) |
|
) м |
Рис. 3.58
Две картины линий скольжения при изгибе надрезанной пластины моментами М в условиях плоской деформации
и р. При этом по минимальному сечению напряжения нарастают по известной формуле
|
|
где радиус r отсчитывается от точки О. Ниже точки С находится поле равномерных напряжений и стф = ax = -2k. Положение точки С можно найти из условия равенства нулю вектора сил, создаваемых ах.
Наблюдаемая экспериментально конфигурация полей пластических деформаций часто близка к этой картине. Но здесь, как и в случае левого поля на рис. 3.51, напряжения ar в точке С имеют разрыв. Нарушаются условия равновесия. Поэтому между логарифмическими спиралями в верхней части сечения и равномерным полем напряжений в нижней части сечения должна существовать некая переходная область.
На правой схеме рис. 3.58 эта переходная область добавлена в виде двух дуг PQ, по которым происходит скольжение. При этом
|
|
|
А Р В |
|
О |
|
А' |
|
В' |
|
Рис. 3.59 Линии скольжения при изгибе консоли |
левая жесткая часть пластины вращается вокруг точки D. По мере уменьшения размера этих дуг правая схема рис. 3.58 приближается к левой.
Нарис. 3.59 показано поле линий скольжения при изгибе консоли.
Видно, что оно состоит из:
|
р |
1) двух областей с равномерным напряженным состоянием
ABCA, где ау = 0; ax = 2k;
2) двух центрированных полей ADCA, в которых напряжения увеличиваются пропорционально углу поворота ф;
3) дуги СС”, которая представляет собой узкое поле простого напряженного состояния (рис. 3.486).
|
'у
|
На рис. 3.60 показано поле линий скольжения, возникающее в полосе толщиной 2h, сжатой жесткими штампами.
Рис. 3.60
Схема линий скольжения и распределение напряжений при сжатии плоского слоя толщиной 2h в направлении оси у
Линии скольжения задаются уравнениями циклоид: для a: x = - h ■ (20 + sin20) + const; у = h ■ cos20; для p: x = +h ■ (20 - sin20) + const; y = h ■ cos20.
В верхней части рисунка показана эпюра напряжений, которые нарастают с удалением от края.