ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ПОПРАВКА НА ОГРАНИЧЕННОСТЬ РАЗМЕРОВ И ФОРМУ ТРЕЩИНЫ
Ограниченность размеров детали и форма трещины в механике разрушения учитываются коэффициентом Х-тарировки, который часто обозначается буквой Y и на который умножается коэффициент интенсивности напряжений, определенный для бесконечной пластины. В случае трещин нормального отрыва, используя формулы (3.61), получаем
|
(3.73) |
ki = Pyy ■'fn~l ■Y.
Имеются англоязычные справочники для определения Y в различных условиях. В табл. 3.1 приведены формулы для наиболее частых случаев.
В последней строчке таблицы даны формулы не для Y, а для вычисления коэффициентов интенсивности напряжений KI(l) у правого конца трещины под действием сосредоточенных расклинивающих сил, приложенных на расстоянии x от центра трещины. Заменив сосредоточенную силу P малым участком dx c распределенным давлениемр, можно вычислить коэффициент интенсивности напряжений у трещин, подверженных внутреннему давлению (например, водорода): P = р ■ dx.
При равномерном давлении р по всей поверхности трещины имеем:
|
|
(3.74)
Интегрирование нужно выполнять отдельно по интервалам отрицательных и положительных значений координаты х.
3.2.4.
|
ДО Й |
ВЛИЯНИЕ ПРОДОЛЬНЫХ СВАРОЧНЫХ НАПРЯЖЕНИЙ НА КОЭФФИЦИЕНТ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
Выпишем отдельно интегралы (3.74), так как ими приходится пользоваться при вычислении коэффициентов интенсивности напряжений от сварочных напряжений. Представим формулу (3.74) в виде
|
|
(3.75)
|
Для положительных значений х: J.<x>=1^*= Ь^=гdx + f |
|
=dx = |
|
Vi27 |
|
x“ |
|
(3.76) |
|
= l ■ arcsin *xj->/12 - x2 . Аналогично для интервала отрицательных значений х: |
|
J2(x>=jJi{Xidx=!#=?dx - У |
|
X |
|
-dx = |
|
Vi2— |
|
(3.77) |
|
= l ■ arcsin xxj + yjl2 - x2. |
Из приведенных формул видно, что в случае равномерного давления:
Ji(l> + Ji(l) = 2 • l • 2.
Подставив это значение в (3.75), получим, что внутреннее давление внутри трещины создает такое же К1, как и внешнее растяжение той же интенсивности:
|
(3.78) |
• l 'К = p 'ЛІК' l.
л/я-l
Снятие с берегов трещины равномерно распределенных растягивающих остаточных напряжений, действующих в сварном шве или околошовной зоне, аналогично приложению к поверхности трещины давления, эквивалентного этим напряжениям. Поэтому для поперечной трещины в сварном шве, если она находится в зоне с равномерными сварочными напряжениями и нет внешней нагрузки, можно записать:
|
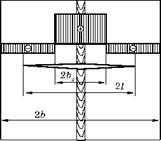
Рис. 3.35 Схема сварной пластины с трещиной и сварочными напряжениями |
Кг =стсв-л/тГ7. (3.79)
Для трещины, показанной на рис. 3.35, нужно интегрировать нагрузку от снятия сварочных напряжений.
Допустим, что в пределах зоны 2bs сварочные напряжения до образования трещины были равны пределу текучести p = ат). Если считать распределение сварочных напряжений симметричным, то тогда на основании условия равновесия за пределами зоны 2bs должны действовать сварочные напряжения:
|
(b - bs) Используя последнюю строчку табл. 3.1 и формулы (3.75)- (3.77), для правого конца трещины рис. 3.35 получим K =-р= • [J2(bs ) - J2 (0) + J(bt ) - Ji(0)] + yjn-l + - f= • J2(l) - J2(bs ) + J1(l) - J1(bs )]. yjn-l Это выражение можно привести к виду ki =Дт=£ х |
|
arcsin blsJ + J1 -b |
|
р2 - ст2св - ' |
|
лік^і f |
|
СТТ • bs |
|
Результаты вычисления KI по 3.36. Видно, что при l > bs коэффи- Однако формула (3.80) не при- шина попадает в зону действия сжимающих сварочных напря- Но на практике кроме сварочных напряжений при распростра- Если по оси абсцисс графика рис. 3.37 откладывать не l/bs, а ний KIp, вызываемого внешней нагрузкойр, от относительной дли- |
|
ны трещины будет определяться формулой KIp = р •yjn-l. |
|
2 ■ bs — • arcsin -s к V l |
|
1 - 2 • |
|
(3.80) |
|
1,772 |
454 |
Ъ = |
5bs |
||
|
Рис. 3.36 Изменение Kj при увеличении длины поперечной трещины в сварной пластине |
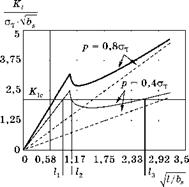
На рисунке эта зависимость для двух уровней нагрузки (р = = 0,4стт и р = 0,8стт) представлена ординатами двух прерывистых наклонных линий.
|
Рис. 3.37 Совместное влияние сварочных напряжений и напряжений от внешней нагрузки на коэффициент интенсивности напряжений |
|
|
Далее к каждой из этих ординат была добавлена зависимость от той же абсциссы коэффициента интенсивности напряжений от сварочных напряжений, вычисленная по формуле (3.80) и показанная на рис. 3.36; полученные суммарные кривые обозначены сплошными линиями — жирной для нагрузки р = 0,8стт и тонкой для р = 0,4стт.
Критерий распространения хрупкой трещины записывается в виде KI > KIC, где KIC — критическое значение коэффициента интенсивности напряжений, определяемое экспериментально путем разрушения стандартных образцов с трещиной. Ориентировочный уровень KIC показан на рис. 3.37 горизонтальной прямой линией.
Из этого рисунка видно, что при р = 0,4стт хрупко начнут распространяться трещины с начальной длиной lt; распространение прекратится, когда трещина достигнет длины l2. При большей длине трещины суммарный коэффициент интенсивности напряжений K1 становится меньше критического, и распространение трещин длиной меньше l3 невозможно. Такие остановившиеся хрупкие трещины достаточно часто наблюдаются в сварных конструкциях в том случае, если они возникают при малых внешних нагрузках. Остановка происходит потому, что вершина трещины попадает в зону сжимающих сварочных напряжений. Из этого же рисунка следует, что при р = 0,8стт остановка трещины становится невозможной.