ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ

КОНСЕРВАТИВНОЕ И НЕКОНСЕРВАТИВНОЕ ДВИЖЕНИЕ ДИСЛОКАЦИЙ

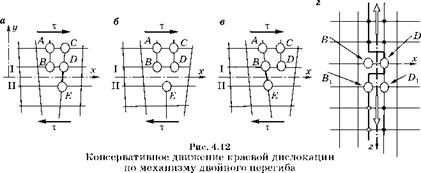
Схема перемещения дислокации при скольжении показана на рис. 4.12.

На рис. 4.12а, б, в показано сечение, перпендикулярное линии краевой дислокации, направленной вдоль оси 2. Краевая дислока­ция в исходном положении (рис. 4.12а) заканчивается атомами лишней плоскости A и B. Под действием напряжений т атомная плоскость I сдвигается относительно плоскости II вправо, и меж­атомная связь D и Е растягивается, а между атомами B и Е укора­чивается. В положении, показанном на рис. 4.12б, усилия, связы­вающие пары атомов BE и DE, равны. Несмотря на то, что эти

усилия очень велики и близки к теоретической прочности метал­ла, внешнее напряжение т, приложенное к атому Е в горизонталь­ном направлении, здесь равно нулю.

При дальнейшем сдвиге упрощенно можно считать, что связь между DE рвется, а между BE восстанавливается до нормальной величины (рис. 4.12в). Это означает, что лишняя плоскость пе­реместилась на одно межатомное расстояние вправо, и ее край совпадает с атомом D. Дислокация перемещается на один шаг ре­шетки b.

От перемещения дислокации из положения (а) в положение (б) не возникает никаких дополнительных возмущений структуры. Суммарный расход энергии равен нулю. Поэтому такое движение дислокации называют консервативным.

На рис. 4.12г эта схема показана в плоскости скольжения (x, z). В исходном положении (рис. 4.12а) все атомы лишней плоскости (атомы B) образуют прямую линию, параллельную оси z. Эта ли­ния показана на рис. 4.12г жирной прямой линией с точками.

К каждому атому этой линии приложена распределенная сила, действующая на дислокацию F = т • b. Кроме того, каждый атом совершает хаотические тепловые колебания. Поэтому практиче­ски невероятно, чтобы под действием усилия т • b все атомы жир­ной линии одновременно, как солдаты по команде, сделали шаг вперед, перейдя в положение, показанное на рис. 4.12в.

Очевидно, что сначала лишняя плоскость перейдет в новое по­ложение D только на одном атоме — на том, в котором фаза мак­симума тепловых колебаний совпала с направлением силы т • b, приложенной к дислокации. В результате на дислокации образу­ется двойной перегиб, показанный на рис. 4.12г жирным прямо­угольным выступом.

Как только двойной перегиб образовался, переход прилегаю­щих к нему атомов из положения рис. 4.12а в положение рис. 4.12б требует меньших локальных усилий, меньшей нужной по фазе амплитуды температурных колебаний. Поэтому двойной перегиб быстро распространяется в стороны, как показано большими свет­лыми стрелками. Когда двойной перегиб распространится на всю длину линии дислокации, она переместится на вектор Бюргерса вправо.

Оценим (грубо) необходимые для этого процесса напряжения. Пусть плотность дислокаций р = 108 1/см2. Тогда расстояние ме­жду дислокациями d = 1/(р)1,2 = 10-4 см. Пусть один двойной пе­региб приходится на длину дислокации, равную d. Тогда один двойной перегиб приходится на площадь F1 = d2 = 10-8 см2. Пусть

для распространения этого двойного перегиба в стороны нужно приложить напряжения St на площади 2 • b2. Тогда с учетом (4.4), необходимые для движения дислокации в a-Fe напряжения:

2,S, b2 2• £-■ (2,481 108)2 E

х, = t =—2Л -------------------- =-- 1,9•іо-7 • E «1,5•lO-3 кГ/мм2

1 F1 108 2(1 + v) 1

Этот пример убедительно демонстрирует, сколь эффективен механизм движения дислокаций двойными перегибами.

Также из схемы рис. 4.12г следует, что если даже один пере­скок атома лишней плоскости происходит со скоростью упругих деформаций, то максимальная скорость пластической деформа­ции в d/(2b) = 10-4/(2 • 2,48110-8) = 2000 раз меньше, чем макси­мальная скорость распространения упругих деформаций.

Первыми сопротивление движению дислокаций в идеальном кристалле исследовали около полувека назад Пайерлс и Набарро. Поэтому сопротивление идеального кристалла движению дисло­кации в литературе часто называют силой Пайерлса-Набарро, или силой трения, и обозначают символом тг.

Некоторое представление о величине х, могут дать эксперимен­тальные результаты по определению сопротивления пластическим деформациям на монокристаллах.

В обзорной книге Д. Мак-Лина «Механические свойства метал­лов» приведены следующие значения для касательных напряже­ний, при которых в монокристаллах при комнатной температуре начинается пластическая деформация:

Однако измеренные экспериментально значения все время уменьшаются с повышением достижимой чистоты монокристал­лов. Кроме того, процесс пластической деформации монокристал­лов связан с термической активацией. Поэтому их сопротивление пластической деформации возрастает с понижением температу­ры. При -200°C хт у молибдена возрастает до 120 кГ/мм2, а у алю­миния — до 10 кГ/мм2.

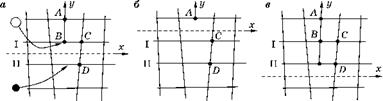
Неконсервативное движение дислокаций возникает в резуль­тате диффузии к лишней плоскости краевой дислокации либо ва­кансий, либо внедренных атомов. Это приводит к перемещению дислокации в направлении оси у, перпендикулярной к плоскости скольжения (x, z).

Если дислокация находится в области сильного объемного сжа­тия у препятствия (например, у твердого неметаллического вклю­чения), то вакансии диффундируют в область сжатия и растворя­ют край лишней плоскости. На рис. 4.13а вакансия показана светлым кружком. Когда она попадает на край лишней плоско­сти, атом B «растворяется». В результате край лишней плоскости перемещается на атом А, как показано на рис. 4.136.

Если же край лишней плоскости находится в области объем­ного растяжения, то туда могут диффундировать межузельные атомы (такой атом показан на рис. 4.13а черным кружком). Когда он попадает в растянутую зону под лишней плоскостью, он ее до­страивает, как показано на рис. 4.13в.

Таким образом, остановленная у препятствия дислокация мо­жет медленно переползать через него. Скорость переползания оп­ределяется скоростью диффузии вакансий, т. е. экспоненциальной зависимостью от температуры. Поэтому вклад неконсервативного движения дислокаций возрастает с повышением температуры ра­боты материала.