ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ИЗМЕРЕНИЯ ДИАМЕТРА ЗЕРНА
Для того чтобы пользоваться в расчетах формулами типа (4.33), нужно знать размер зерна. Обычно диаметр зерна измеряют на микрошлифах — как средний его диаметр в плоскости шлифа. С этой целью достаточно определить количество зерен, видное на единице площади, определить среднюю площадь одного зерна, и, считая зерно квадратным или круглым, найти его размер.
Данное решение основано на предположении, что на металлографическом шлифе виден действительный диаметр зерна. На самом деле это далеко не так. Если предположить, что все зерна
|
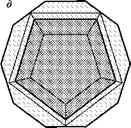
Рис. 4.23 Конфигурация некоторых сечений пентагондодекаэдра |
|
|
|
|
|
|
изотропны, то на линии стыка трех зерен (на рис. 4.23а эта линия выходит на плоскость чертежа в точке 0) атомы при температурных колебаниях находятся поочередно то в решетке первого зерна, то второго, то третьего.
Однако чем больше угол, который занимает данное зерно, тем большее время граничные атомы проводят в этом зерне. В это время следующие атомы становятся граничными. В результате граница перемещается в точку 0*. Поскольку больший угол обычно имеет большее зерно, говорят, что крупные зерна «пожирают» мелкие. Так будет продолжаться до тех пор, пока все двугранные углы зерен не станут равными 2л/3 = 120°. Такими двугранными углами обладает додекаэдр (рис. 4.236). В первом приближении предположим, что все зерна имеют форму додекаэдров, хотя из них нельзя построить сплошного тела.
Если в поликристалле из этих зерен сделать произвольный разрез, то можно предположить, что сечения различных зерен будут проходить по различным, случайно ориентированным плоскостям. Чтобы получить представление о форме данных сечений, на рис. 4.23 показаны формы, получаемые при трех возможных ориентациях плоскостей разреза.
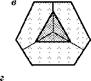
Если срезается вершина додекаэдра (рис. 4.23в), то зерна на шлифе могут иметь либо форму треугольников малого размера, либо шестиугольников, если разрез прошел ниже.
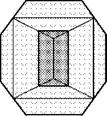
Если срезается ребро додекаэдра (рис. 4.23г), то на шлифе получаются прямоугольники или восьмиугольники.
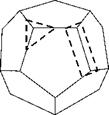
Если срезается грань додекаэдра (рис. 4.235), то на шлифе должны быть видны либо пятиугольные, либо десятиугольные срезы зерна.
Только на десятиугольных срезах заметен действительный размер этого додекаэдра. Все остальные сечения имеют меньший размер.
Из этих рассуждений следует, что измеряемый на шлифах размер зерен не может считаться их истинным диаметром, он всегда меньше его. Но вероятно, что средний размер зерна, измеренного на шлифе, будет пропорционален истинному размеру зерна. Поэтому теоретические формулы, типа формулы (4.33), обязательно должны содержать эмпирическую поправку не только на статистические характеристики распределения зерен по диаметру йз и их ориентировки 01 и 02, но и эмпирическую поправку на отличие истинного диаметра зерна от измеренного его диаметра.
Как правило, величины, рассчитанные с помощью теории дислокаций, верны с точностью до постоянного множителя, который определяется экспериментально.