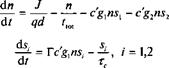Оптоэлектроника

Конкуренция мод: перекрестные модуляторы

В дополнении 11.Д мы видели, что вблизи порога полупроводниковый лазер может генерировать в многомодовом режиме несмотря на то. что усиливающая среда яв­ляется однородной. При достаточно сильном возбуждении настолько выше порога, что спонтанной эмиссией можно пренебречь по сравнению со стимулированным излучением, лазер, в конце концов, вновь приобретает одномодовый характер. Сейчас мы изучим этот феномен более детально. Мы покажем, что этот эффект может быть понят с учетом перекрестного насыщения, при этом мы увидим, каким обра­зом этот эффект используется в оптоээлектронных приборах, а именно в модулято­рах с перекрестным усилением.

Мы начнем с (13.Д.7), дающего динамические уравнения для лазерного резона­тора в многомодовом режиме. Для упрощения расчетов предположим, что лазер функционирует в режиме намного выше уровня прозрачности так, что п » ntr и величиной Rspon можно пренебречь, при этом существуют лишь две моды. В этом случае уравнение (13.Д.7) может быть записано в виде:

Напоминаем, что б и п есть соответственно концентрация электронов и плотность фотонов, / — плотность тока накачки, с1 —толщина активной области; ^о1 — полное рекомбинационное время жизни; г — время жизни фотонов в резонаторе; gi — дина­мическое усиление; с' — скорость света в среде, а Г — коэффициент ограничения. В стационарном состоянии 13.11) дает концентрацию электронно-дырочных пар:

Здесь: п0 = Л{о1/дс1 есть концентрация электронно-дырочных пар холодного резона­тора, что приводит к усилению среды <7 для моды / в виде:

С, =--------- Яа------

1 + £,5, + £2Б2

Здесь <7.0 = Гс'£.л0 есть усиление холодного резонатора и е. = Как и в допол­

Нении 11.Е и в соответствии с общепринятой практикой члены е обозначают вели­чину, обратную плотности насыщения фотонов ^ для которой величина усиления уменьшается вдвое (смотрите главу 2). В последнем уравнении (13.13) мы видели, что усиление на одной длине волны может быть насыщено пучком накачки на различных длинах волн. Этот эффект используется в модуляторах с перекрестаным усилением. Рассмотрим и объясним сейчас функционирование этого прибора.

Рассматриваемый прибор способен преобразовывать модулированный сигнал с длиной волны Л2 в модулированный сигнал с длиной волны Лг В завершение этого полупроводниковый оптический усилитель (типа МОРА) накачивается непрерыв­ным пучком на длине волны Л2 с интенсивностью, приближающейся к плотности насыщения (смотрите рис. 13.И. 1). Дополнительный сигнал на длине волны Я1 на­сыщает среду (смотрите 13.3.3), при этом на длине волны Л2 наблюдается ослабле­ние усиления. Таким образом выходная мощность на длине волны Л2уменыиается, когда увеличивается входная мощность на длине волны Лг Таким образом, сигнал, изначально передаваемый на длине волны Я,, отображается «негативно» в световом пучке на длине волны Л2 (смотрите рис. 13.И. 16).

Дадим теперь краткое описание динамического поведения этого лазера с уче­том конкуренции мод 1 и 2. Для этого мы предположим, что лазерное усиление <7 находится в стационарном режиме в то время, как оптические моды не находятся в этом режиме. Это приводит к /1о1 < г, что имеет место в лазерах на основе атомных переходов, но не в полупроводниковых лазерах. Хотя и нет особой необходимости

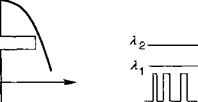
В такой аппроксимации, без нее будут скрыты физические аспекты рассматривае­мой задачи, которые мы хотели бы представить в явном виде.

Подставляя выражение для насыщенного усиления (13.И.3) в (13.И. 1), получаем:

5. =___________ £»______________ / = 1,2

1 +ех8х+е2Б2 'г/ ’ (13.И.4)

Предположим, что среда слегка насыщена (что предполагает ер. « 1), обеспечивая ограниченное разложение (13.14):

5, = - 6,25^2

Б2 = а2Б2 - 62,5,52 - К2б] (13.И.5)

В это последнее выражение мы ввели следующий параметр:

<*/ = <7/о “ —» К; = &Iе» °и =

Гс (13.И.6я)

Эти члены есть ничто иное, как полное усиление (являющееся результатом конку­ренции между резонаторным усилением и потерями, членом автонасыщения и чле­ном автоперекрестного насыщения). В контексте аппроксимации (13.И.5) мы ви­дим, что имеются два стационарные решения для плотности фотонов для этих двух уравнений:

(а, - /с,5, -0|252>, = о

(а2 - 0215, - = 0 (13.И.66)

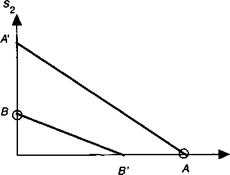
Легко показать, что линии а. = к р. + в. р. не пересекаются. Таким образом, решения лежат в точках пересечения линий, определяемых условием (13.И.66), и осей координат, как это представлено на рис. 13.И.2: точка А ($20= 0 и 510 = осх/к^ и точка В (у10 = 0 и 520 = а2/к2). Мы увидим, что только одна из этих двух точек дает устойчивое решение (13.И.5).

Вблизи точки А для плотности фотонов может быть записано разложение в виде 52 = Зб2 и 520 = а2/к2. После чего дифференциальные уравнения линеаризуются и могут быть записаны в матричном виде:

Мы видим, что решение будет устойчивым только, если:

А2 < в2Х

Кх

С учетом определений (13.3.6) это соответствует условию:

С, о > С20 (13.И.9)

Другими словами, хотя положительное усиление в резонаторе имеет место для обеих длин волн, предпочтительной для лазера в стационарном состоянии будет генерация на моде с наибольшим усилением (отсюда и термин конкурен­ция мод). Используя тот же самый формализм, мы могли бы показать, что нео­днородно уширенная среда будет характеризоваться многомодовым стационар­ным функционированием.

Свойства основных полупроводниковых материалов

[1] Символ л обычно используется тогда, когда может возникнуть путаница в различии между физи­ческой величиной ( например положением г) и соответствующей ей квантовой наблюдаемой (?).

[2] Примечание ред. : строго говоря энергии фотонов Н соп = 2 эВ соответствует оранжевый цвет

Свечения.

[4] - 5>„ - ( - - 777^г-т (2.87)

П=0 п=О С 1

Подставляя уравнение (2.87) в условие (2.86б), получаем распределение Бозе - Эйнштейна:

[5] В контексте этого раздела поглощение не может быть отрицательным. Единственным случа­

Ем, когда сила осциллятора отрицательна, является ситуация, при которой Орне является основным уровнем (т. е., если Еу< Е{), в случае чего уравнение (3.44) должно отслеживать величины заселенности

[7] По-видимому, существует столько же вариантов нормировки Фурье-образа, сколько суще­ствует и авторов. Некоторые из них используют коэффициент 1/У2я, другие 1/2#для перехода от со к и Третьи же авторы используют эти коэффициенты для перехода от I к со

[8] V

-1 Ч)

[9]0*0* о* о» о» о*о*о*о*о*о «о о *о *0*0

0*0* О* О» О» О* О* 0*0*0 *о *о О О *0*0*

*0*0* о* о* о» о* о * о * о • о *о «О О «О *0*0

0*0*0* О» О О* О* 0*0*0 *о *о О «О *0*0*

*0*0* о* о* о» о*о*о*о*о*о «О О «О *0*0

0*0*0* о. О О* О* 0*0*0 *о *о О О *0*0*

Ю - фонон

Рис. 6.Б.30. Картина смещения атомов в двумерной решетке, содержащей два типа атомов. Поперечные оптические (ТО) и продольные оптические (Ь0) фо­ноны представлены соответственно в верхней и нижней части рисунка.

[10]3 = 2*, - *» =

[11] (7.В.6)

■Дй^ахт

Глубина скин-эффекта

[12] модель предсказывает спектральную зависимость типа Л2 для коэффициента поглощения, что не подтверждается экспериментом. В общем случае, коэффици­ент поглощения а пропорционален степенной зависимости Л с показателем, отлич­ным от 2 (а= const х Лр, где р изменяется в диапазоне 1,5—3);

Поведение обеих волн носит особенно простой характер, когда удовлетворяет­ся брэгговское условие (АР = 0), т. е. когда волновой вектор решетки равен коэф­

Фициенту я/А волноводной волны. В этом случае решение (9.Б.10я) принимает простой вид:

[14] (г)=^ ~ф1^^ ^

[15] -

[16] =------- Na, d2<z<d2+d

Dz 8

[17] Постоянная времени из-за переноса носителей через область пространственного за­ряда. Протяженность SCR при приложении потенциала в 1 В составляет величину порядка 1 мкм, при этом напряженность электрического поля в этой области составляет 104 В см-1. Даже в материале со сравнительно малой подвижностью (например, ju = 102 см2 В-1 с-1) это соответствует скорости 106 см с-1 и таким образом времени пролета носителей 100 пс и частоте отсечки 10 ГГц.

Первые два ограничения являются неприемлемыми для большинства телеком­муникационных применений, требующих ширины полосы частот в десятки ГГц или более того. Предназначенные для этих применений р—/—я-диоды (смотрите рис. 11.13) обладают собственной областью с большой шириной W заключенной между сильнолегированными областями п - и р-типа проводимости.

Эти диоды были рассмотрены в разделе 10.2 (смотрите зонную диаграмму на рис. 10.А.2). Такая приборная структура обладает рядом преимуществ:

(и

[19] mr

[20] Фотопроводник с рекомбинацией. Мы можем предположить, что излучатель-

Ное время жизни носителей распределено в соответствии с процессом Пуассона:

[22]2vG = 2qAvqG(x0)AAx

& =2?Дга„/„(*о)** (11. А. 54)

[24] сЬ = собЬ, бЬ = бшЬ

[25]

[26] Прим. ред.: В данном случае под / понимается прямой ток смещения, а не его плотность.

[27] Прим. ред.: для СаАз0 35Р0 65^ = 2 эВ.

[28] ,

+ -—1п ' 2Ь

Фотонное время жизни в полупроводниковом резонаторе определяется выраже­нием (смотрите (4.23а, б)):

[29] бЬ = сЬ = собЬ.

[30] Прим. ред.: Это утверждение не совсем корректно, т. к. нанесение полупрозрачных металличес­ких зеркал на поверхность полупроводниковых слоев возможно и используется в технологии ЛД.