Оборудование заводов по переработке пластмасс

Распределение напряжений сдвига, поле скоростей и объемный расход при поступательном течении

В случае изотермического режима исходная система уравнений равновесия подвергается дальнейшим упрощениям. Вследствие неизменности температуры величина dxzyldz—0, и уравнения равновесия сводятся к виду

ДР дхух дР _ dxyz

Дх ду ' дг ду

Из второго уравнения следует, что P=P(x, z). Поскольку ле­вые части уравнений (5.56) зависят только от х и z, а правые только от у, то

DP dxyx dP dxyz

Последовательно интегрируя (5.57), получим для компонен­тов девиатора тензора напряжений выражения

DP dP

%ух = - аГУ-С9 хуг = -^у-Сь (Ь. ЬЬ)

Для функции Px, z имеем:

DP dP

P(x, z) = -^-z---^-x = C2z--ClX (5.59)

- Полученные результаты показывают, что градиенты давле­ния в рассматриваемом случае плоского изотермического тече­ния постоянны по всему потоку.

Из уравнений (5.58) следует, что напряжения сдвига, дей­ствующие во взаимно перпендикулярных плоскостях хоу и zoy, распределены линейно, т. е. зависят только от у.

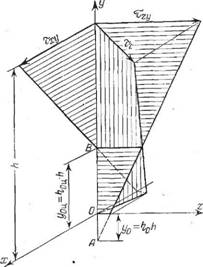
Для большей наглядности изобразим пространственную эпю­ру напряжений сдвига, действующих на верхнюю грань элемен­тарных объемов. Такая эпюра распределения тангенциальных напряжений (рис. 5.23) показывает, что в каждом из составляю­щих течений существует сечение нулевых напряжений. При этом, поскольку в циркуляционном течении всегда существуют обла­сти с различным направлением движения и, следовательно, гра­диент скорости меняет знак, то сечение, в котором txy = 0, рас - лолагается внутри канала.

Циркуляционное течение возникает вследствие того, что на­правление относительного движения между червяком и кор­пусом не совпадает с осью винтового канала. Поэтому ве­личина действующих в плоскости хоу напряжений сдвига зави­сит от угла подъема винтового канала, возрастая с его уве­личением. В случае ньютоновской жидкости взаимное влия­ние ' поступательного и циркуляционного течений ограничива­ется только этой зависимостью.

Считая течение в пределах «сечения толщиной dz изотермиче­ским, воспользуемся уравнением (5.49) и выразим %ух й %yz в (5.58) ■через компоненты тензора скоростей деформаций. При этом уравнения

(5.58) с учетом (5.50) примут вид: (-£*.-*) <'■"'=

Fc-HS»-*) (5'м"

Интегрируя эти уравнения и оп­ределяя постоянные интегрирования из граничных условий (5.53), получим выражения, описывающие поля ско­ростей поступательного и циркуляци­онного течений.

Рис. 5.23. Типичная пространственная Диаграмма распределения напряже­ний сдвига в канале червяка. Пояс­нення в тексте.

Если пренебречь тормозящим влиянием стенок, то распреде­ление скоростей в поступательном течении описывается выраже­нием

Uzy yh-y* dP

~~h~~ 2rj--------- dT (5'61>

Здесь первое слагаемое описывает распределение скоростей вынужденного потока, второе — потока под давлением.

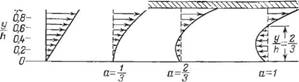
Распределение скоростей вынужденного потока имеет форму треугольника, а распределение скоростей потока под давлени­ем— форму равнобокой параболы. Фактический профиль ско­ростей поступательного потока образуется в результате вектор­ного суммирования в каждой точке скоростей обоих потоков. Эпюры результирующего профиля скоростей, соответствующие различным значениям потока под давлением, приведены в ниж­ней части рис. 5.24.

Объемную производительность зоны дозирования получим, интегрируя выражение (5.61) по всей высоте канала:

А

>=wjvzdy : =

Здесь первое слагаемое — объемный расход вынужденного потока qa, второе — объемный расход противотока qp.

H-f/z-H Поверхность корпуса

0,8- Вынижден-—у

У 0,6- ный г—у А-— Противоток

OA- поток tt fc^ Г v

0,2- vzcL ^ н

Безразмерные коэффициенты Fd и Fp учитывают влияние стенок, проявляющееся в уменьшении эффективной ширины ка­нала: ■

Значения Fd и Fp, рассчитанные по уравнениям (5.63) и -■(5.64), при изменении hjw в интервале от 0 до 2 приведены на рис. 5.25.

Введем безразмерную характеристику поступательного тече­ния:

Lqd h*F„dP/dz

В общем случае, если к обоим концам червяка приложены произвольные внешние давления, величина а может принимать любые — как положительные, так и отрицательные значения. Однако, если внешние давления отсутствуют, значение а изме­няется от нуля до единицы. При этом для червяка, работающе­го в режиме свободного выхода, а = 0; для червяка, работающе­го с полностью закрытым выходом, но при отсутствии утечек, «=1; из-заj существования утечек а<С 1. Если давление на вы­ходе из зоны дозирования меньше, чем на входе, то а<0.

Используя этот безразмерный параметр, можно представить выражение (5.62) в виде

Q = qd{ — a) (5.66)

Если подставить геометрические характеристики червяка в (5.62), получим выражение

1 dP

Q = —Р —- - зг

Здесь а — коэффициент подачи вынужденного потока, чис­ленно равный половине объема одного витка:

А = 0,5ji2D2/2[1 — ie/(nD tg ф)] sin ф cos фFd

(5.68)

Коэффициент подачи потока под давлением р равен

Р = siDhs [1 — ieftsiD tg ф)] sin2 (fFp ■ (5.69)

Профиль скоростей в циркуляционном течении определяется выражением, аналогичным (5.61). Если воспользоваться безраз­мерным отношением расхода вынужденного потока к расходу потока под давлением в циркуляционном течении, положив его равным единице (утечки пренебрежимо малы), то распределе­ние скоростей циркуляционного течения будет описываться вы­ражением

VK=Ux(2,y*/h*-2y/h) (5.70)

Выражение (5.70) показывает, что распределение скоростей в циркуляционном течении не зависит от давления в головке и полностью определяется размерами канала и скоростью враще­ния червяка.

Полученные выше выражения позволяют рассчитать объем­ный расход в любом сечении винтового канала при заданных значениях температуры и локального градиента давления. Воз­можен также и обратный вариант расчета — определение ло­кальных значений градиентов давления при заданных объемном расходе и температуре. При этом все расчеты основаны на при­менимости изотермического приближения, справедливого в пре­делах участка канала малой длины, например в пределах одно­го шага расчета (Дz^.D/10).