Оборудование заводов по переработке пластмасс

Продолжительность стадии охлаждения

Время, необходимое для охлаждения изделия до температуры, при которой его можно удалить из формы, оказывает домини­рующее влияние на общую продолжительность цикла и, следо­вательно, на фактическую производительность литьевой ма­шины.

Охлаждение находящегося в форме изделия происходит в основном за счет теплопроводности. Поэтому при теоретическом анализе процесса охлаждения реальных изделий следует ис­пользовать результаты, полученные в теории нестационарных тепловых процессов. В настоящее время получено достаточно большое число решений одномерных уравнений теплопровод­ности для тел различной геометрической формы.

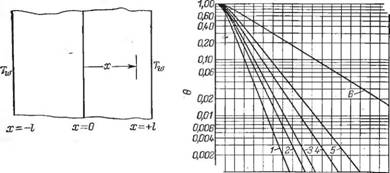
В качестве примера можно рассмотреть задачу об охлаждении тонкой пластины (рис. 7.38).

Принимая, что температура на поверхности изделия немедленно становит­ся равной температуре стенки формы, можно воспользоваться для анализа про­цесса охлаждения тонкой пластины решением Карлсоу и Егера, полученным для граничных условий третьего ряда (заданы температура и коэффициент теплоотдачи на поверхности контакта).

Для случая, когда в начальный момент температура цластины Т0 во всех точках одинакова, а коэффициент теплоотдачи очень велик (это эквивалентно

Ц2 Q4 О, Б 0,8 1,00 1,20 1.W 1,60 1,80 Fo

Рис. 7.39. Номограмма зависимости безразмерной температуры Є от критерия Фурье Fo:

/ — центр шара; 2— цилиндр (/ = D); 3 — куб; 4— цилиндр (L = оо); 5 — стержень квад­ратного сечения 6 — середина бесконечной пластины.

Заданию постоянной температуры на стенке), решение имеет вид Є = Ф (1/2F01/2) = Ф (х/2 ~[/ai) Здесь 0 — безразмерная температура, равная

То — Txt

0= ■

То — Тш

Где Tw — температура стенки формы (см. рис. 7.38).

Критерий Фурье Fo равен Fo=at/x2 (где а — коэффициент температуро­проводности) . Функция ошибок Ф (х) равна

Ф (х) = erf х

Где

/зt J6 dS і/л (

Средняя температура в пластине в момент времени t равна

А(2п - f - I)2 л2Г 4I2

П=О

Где I — полутолщина пластины.

Для прикидочных расчетов удобно пользоваться номограммой зависимо­сти 0 от Fo (рис. 7.39).

Использование этого решения и приведенной на рис. 7.39 номограммы состоит в следующем.

1. Определив на основании результатов лабораторных испытаний темпе­ратуру теплостойкости, рассчитывают по формуле (7.8а) безразмерную темпе­ратуру в центре пластины (х=0).

2. По номограмме (см. рис. 7.39) определяют безразмерное время (при­нимают, что а=оо).

3. Подставляя значение коэффициента температуропроводности а и полу­толщины стенки I, определяют фактическое время охлаждения:

I= I2 Fo/a (7.11)

Наибольшее время необходимо для охлаждения наиболее массивных мест изделия. Номограммы, описывающие зависи­мость безразмерной температуры от критерия Фурье (безраз­мерное время на оси бесконечного цилиндра' и в центре шара), также приведены на рис. 7.39.

Расчет продолжительности охлаждения реального изделия сводится, таким образом, к расчленению изделия на ряд про­стых по геометрической форме частей и определению продол­жительности охлаждения каждой из этих частей в отдельности. При этом следует стремиться к тому, чтобы разница между минимальным и максимальным значением времени охлажде­ния различных частей детали не была слишком велика.

Для приближенной оценки продолжительности охлаждения можно воспользоваться упрощенной зависимостью:

Т0 = 0,08 (l2/a) lg (0,7850) (7.12)

При использовании любого из описанных методов расчета нужно иметь в виду, что теплопроводность материала зависит от температуры. Поэтому при расчетах следует использовать ее среднее значение, определенное для интервала температура впрыска -— теплостойкость.