Оборудование заводов по переработке пластмасс

Приращение давления в зоне питания

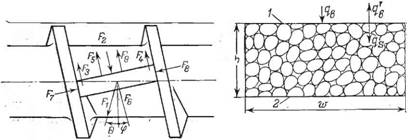
Для определения давления, развивающегося в зоне питания,, рассмотрим силы, действующие на элемент твердой пробки (рис. 5.21).

Сила Fi — это сила трения, действующая со стороны корпу­са на пробку и заставляющая ее двигаться по червяку. Она про­порциональна давлению со стороны пробки на корпус Р и дей­ствует под углом 0 к плоскости, нормальной к оси червяка:

F1 = foPtpudz = fbKsPwdz (5.10)

Осевая и тангенциальная компоненты Fi соответственно рав­ны

Fii = fhPi, wdz sin Є (5.11)

Fie = fbPbwdz cos в (5.11a)

Пара сил F2 и Fe представляет собой реакции отброшенных кусков пробки, действующих на рассматриваемый элемент. Их можно определить, умножив удельное давление на площадь по­перечного сечения канала.

Если, как это часто бывает на практике, глубина канала плавно уменьшается (конический сердечник червяка), то

F2 = hwP (5.12) Fe = (P + dP)(h — ydz)w (5.12a)

Вычитая F2 из F6, получим:

Fe — F2=w(h + dh) dP— wPydz (5.13)

Силы F7 и Fs — это нормальные силы, действующие со сто­роны стенок канала червяка на пробку. Сила Fs равна

F8 = Pxhdz = PKJidz (5.13а)

Где Ks=Px/P, определяется из (5.4).

Сила F7 — это сила, с которой на пробку давит толкающая стенка канала. Она складывается из двух частей: силы, рав­ной силе Fа, и силы F*, уравновешивающей все остальные:

F7 = Pxhdz + F* (5-14)

Разность между F7 и F8 равна неизвестной силе F*.

В червяках с коническим сердечником со стороны сердечни­ка на пробку действует дополнительная нормальная сила Fg, равная

F9 = P, ws sin (arctg x) dz ~ PKswsydz (5.15)

Сила трения F3, действующая на пробку со стороны толка­ющей стенки червяка, равна

F3=(Pxhdz + F*)fs (5.16)

Сила трения F4, действующая на пробку со стороны перед­ней стенки канала, составляет

F4 = PKhfsdz (5.17)

Сила трения Fs, действующая на пробку со стороны дна ка­нала, равна

F5 = Pswdzfs cos (arctg у) « PKswdzfs (5.18)

Где Ps — нормальное давление, действующее со стороны стенок канала червя­ка на пробку.

При нормальной работе экструдера сумма проекций всех сил на ось червяка должна быть равна нулю:

Fи + (Fв ~ FJt - 7 - fs)l + Fst + hi + F5I +Fsl = 0 (5.19)

Осевые^ компоненты сил F2—Fg получим, умножая их на sincp, sin ф, віпфа. Умножая каждую из действующих сил на со­ответствующее значение радиуса, получим уравнение равнове­сия в моментах сил относительно оси червяка:

D D D D

Fid 2 ~(Fe — Fih~2~—— Fs)e~2~ —— D Ds Ds

Тангенциальные компоненты сил F2—Fg получают умноже­нием модуля соответствующего вектора силы на совф, совф или cos фв.

Преобразуя уравнения (5.19) и (5.20), исключая неизвест­ную нормальную силу F* и выполняя интегрирование, получим следующее выражение для определения приращения давления на участке длиной Az=z2—Zi

Z2

^expf dz (5.21)

Zi

Здесь P] — давление на входе в участок длиной Az; Рг — давле­ние на выходе;

Ах = wfbKs sin 6 — sin cp - j - 2tiKsfs sin cp +

+ wfsKs sin ф (1 + x//s)/(l + X2)1/a (5.22}

A2=hw sin ф (5.23)

B1 = wfbKb cos 0 + cos ф D/D —

- 2hKsfs sin <p ctg ф D/D - wKsfs (1 + %lh) D (5-24>

B2 = wh cos ф D/D (5.25)

К = Ъ sin<p + /scoscp (5 26)

U COS ф--- /s sin ф

Где ф = arctg [t/(nD) и ф5 = arctg [і/(яД5)].

Давление в зоне питания определяется по формуле (5.21) численным методом. В практических расчетах можно заменить конический сердечник ступенчатым цилиндрическими и, поло­жив в выражениях (5.22) —(5.24) %=0, вычислять-давление по более простой формуле:

Рг^Рм-ЪЁТйГ* <5-27>

Если гидростатическое давление в пробке подчиняется за­кону Паскаля, то Ks = Kb = !•

Изменение скорости движения пробки, вызванное изменени­ем плотности гранулята, учитывается при помощи эмпирической: зависимости вида

It^i (5.28)?

Где р —плотность пробки при давлении Р; р„ — предельное значение плотно­сти хорошо спрессованного полимера; р0 — начальная плотность гранулята;. с — эмпирический коэффициент, равный в случае полиэтилена низкой плотно­сти 0,16 МПа-1.

Изменение плотности приводит к изменению угла трения Є„. который рассчитывается по формуле (5.9) при заданном значе­нии массового расхода.