Оборудование заводов по переработке пластмасс

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ПРОЦЕССЕ КАЛАНДРОВАНИЯ

Производим и продаем электроприводы ЭТУ, ЭПУ для двигателей постоянного тока, тел./email +38 050 4571330 / rashid@msd.com.ua

Привод ЭПУ 25А с дросселем - 5500грн

Математическое описание процесса каландрования полностью подобно описанию процесса вальцевания, приведенному в гл. 4. Основные теоретические результаты были получены именно при анализе процесса каландрования. Поэтому для описания кине­матики потока, возникающих в зазоре напряжений сдвига, распорных усилий и мощности, необходимой для привода вал­ка, можно пользоваться зависимостями, выведенными в гл. 4. При этом следует иметь в виду, что ширина листа при перехо­де полотна с одного валка на другой в связи с уменьшением зазора несколько возрастает (рис. 6.9), так', чтобы величина объемного расхода оставалась неизменной. Поэтому при рас­чете всех интегральных характеристик процесса (распорные усилия, действующий на валок крутящий момент, мощность привода каждого валка) необходимо учитывать это увеличение ширины.

Поскольку внешние валки контактируют только с одной по­верхностью зазора, на которой действуют напряжения сдвига, а внутренние — с двумя, а также и потому, что ширина листа на внешних валках меньше, мощность, необходимая для при­вода центральных валков, превышает мощность, требуемую для привода внешних, примерно в 2—2,5 раза. Типичное распреде­ление мощности двигателей привода для четырехвалкового ка­ландра, выполненного по схеме рис. 6.2, з: 0,14/0,33/0,36/0,17.

Математическая модель неизотермического каландрования строится в предположении, что реологические свойства полимера могут быть описаны степенным уравнением. Кинематическая картина движения и все упрощающие предположения остаются такими же, как в случае симметричного вальцевания ньютоновской жидкости. С учетом этих допущений математическая модель, в которую входят уравнение движения, уравнение неразрывности, уравнение теплопроводности, реологическое уравнение состояния, а также начальные и граничные условия, имеет вид

DP дхгц дь'х , dvu

TOC o "1-3" h z - W = ~W (6Л) + = ° (6-2>

Їх., I dvx І1/" . dvx

=I~dy J (6-3>

ДТ a''T dvx

К/Л - Q - = я ~дхТ (6-4>

Где р, Ср и k — плотность, удельная теплоемкость и коэффициент теплопровод­ности расплава соответственно; остальные обозначения приведены выше.

Начальные и граничные условия:

Х=х±; Р = 0; Т = т0;

Х = —х2; Р = 0; хху = 0; vx = U

(6.5)

Dvx Л дТ

У = 0' ж = т^ = 0; Ж = 0

У — ±h vx = U; Г = ГШ; Г0=ГШ; £У=соЯ

Решение системы уравнений (6.1)—(6.4) с учетом начальных условий (6.5) позволяет рассчитывать как температурные поля, так и все кинетостати - ческие и энергетические параметры процесса. Система уравнений (6.1) — (6.5), представляющая полную математическую модель неизотермического каланд - рования, состоит из нелинейных дифференциальных уравнений в частных про­изводных. Аналитическое решение такой системы невозможно. Поэтому для расчета температурных полей и кинетостатических характеристик использовали численные методы.

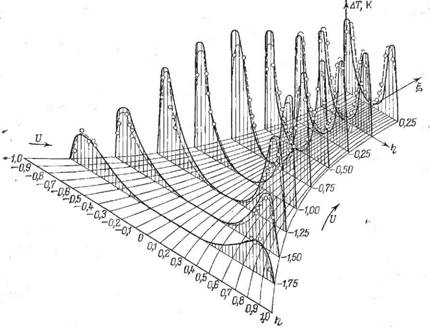
Типичный пример рассчитанного температурного поля для каландрующего зазора лабораторного каландра представлен на рис. 6.10. Особенностью профиля температур является на­личие трех экстремумов — двух максимумов и одного миниму-

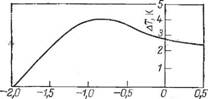
Рис. 6.11. Продольное распределение экстремального приращения темпера­туры в зоне деформации каландра.

Ма. Оба максимума располагаются в непосредственной близо­сти от поверхности валков, а минимум — в центре зазора. Та­кая форма температурного поля обусловлена тем, что величина мощности диссипации достигает максимального значения на поверхности валков, а в центре тепловыделение отсутствует. В результате теплопроводности часть тепла отводится к вал­кам, максимум температуры смещается на некоторое расстоя­ние внутрь зазора. Таким образом, теплопроводность играет существенную роль только в непосредственной близости от по­верхности валков и проявляется в некотором выравнивании тем­пературного поля.

По мере продвижения полимера вдоль зазора максимумы температур вследствие процесса теплопроводности смещаются вглубь, а в центре наблюдается незначительное повышение температуры. Поскольку теплопроводность полимеров невели­ка, безразмерная координата максимума температуры в потоке каландруемого материала составляет rj= ±0,8—0,65.

Возрастание температуры в середине листа, как правило, не превышает 1—2'°С. Наиболее интенсивный разогрев происходит на начальном участке области деформации (рис. 6.11). Затем температура несколько снижается и сохраняется в дальнейшем примерно на одном уровне. Это объясняется снижением дисси - пативных тепловыделений в сечении максимального давления (напряжения сдвига равны нулю) и некоторым выравнивани­ем температурного поля вследствие теплопроводности. В ос­новной массе каландруемого материала профиль температур­ного поля определяется процессом конвективного переноса теп­ла.

Неравномерный характер распределения температур следу­ет учитывать при выборе режимов каландрования термочувст­вительных полимеров. Расчетные и экспериментальные данные показывают, что локальные приращения температуры в сечении каландруемого листа при высоких скоростях каландрования высоковязких смесей могут достигать нескольких десятков гра­дусов. Можно полагать, что именно локальный разогрев явля­ется причиной таких видов наблюдающегося при каландрова­нии брака, как пористость и пузыри, возникающие вследствие термодеструкции ПВХ при каландровом методе получения ли­нолеума и лимитирующие максимальную скорость каландрова­ния.