Оборудование заводов по переработке пластмасс

Математическое описание работы зоны дозирования

Для удовлетворительного описания процесса экструзии матема­тическая модель течения расплава в пределах зоны дозирования должна учитывать основные особенности процесса: существова­ние аномалии вязкости; взаимное влияние циркуляционного и поступательного течений; влияние тепла, выделяющегося в ре­зультате внутреннего трения, и теплообмена с окружающей сре­дой на температуру и эффективную вязкость расплава.

Очевидно, что для работы экструдера безразлично, враща­ется ли червяк внутри неподвижного корпуса или, наоборот, корпус вращается относительно червяка. По этой причине для упрощения будем считать корпус вращающимся, а червяк не­подвижным. Расположение связанной с червяком неподвижной системы координат показано на рис. 5.19. Ввиду малости отно­шения глубины винтового канала к радиусу (h/R<i0fi5) можно пренебречь кривизной винтового канала и развернуть его на плоскость так, как это показано на рис. 5.22. При этом корпус будет изображаться бесконечной плоскостью, движущейся над развернутым каналом в перпендикулярном оси I направлении.

Течение считаем установившимся. Массовыми силами и си­лами инерции пренебрегаем. С учетом этих допущений уравне­ния равновесия в напряжениях примут вид

ДР дх иу дх, х _ дР дхУ7 дхиг _ „ ,

Среду считаем несжимаемой:

Дух дуу дуг дх > dy дг

Компоненты тензора напряжений определяются выражением [ gv. dvj

= і, І = х. у,г (5.49)

Для построения модели, допускающей аналитическое реше­ние, сделаем следующие допущения.

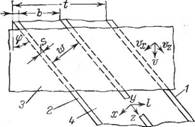
Рис. 5.22. Развертка винтового канала червяка на плоскости:

]__ стенка канала; 2 — развертка червяка;

З — поверхность корпуса; 4 — канал.

1. Течение в направлении оси у существует только в непосред­ственной близости к стенкам ка­нала. В остальной части сечения канала течение в направлении оси у отсутствует (vy = 0).

2. Размеры канала по всей длине постоянны, следовательно, значения vx и vz не зависят от z.

3. Температурный градиент в поперечном направлении из-за наличия циркуляционного течения пренебрежимо мал по срав­нению с температурным градиентом в продольном направлении. Следовательно, дТ/дх=дТ/ду=0; дТ/дгфО.

Благодаря большому отношению ширины винтового канала к его глубине, учитывая допущение 2, а также особенности цир­куляционного течения, можно принять, что на некотором рас­стоянии от стенок канала скорости vx и vz не зависят и от х. Следовательно

Dvz

■ = 0

Дх

Дь'п

Dz = df— <5-50>

Для описания температурной зависимости вязкости исполь­

Зуем выражение:

Ь (г-г6)

(5.51)

■ температурный коэффици-

Где г)о — вязкость при температуре плавления; ент вязкости.

Уравнение энергетического баланса, составленное для уста­новившегося режима в предположении, что все теплофизические характеристики не зависят от температуры, имеет вид ■ дГ д2Т dvx dvz

РсР°*~дГ = ~km + ~W ( ]

Где Ср — теплоемкость расплава; Т — температура расплава (остальные обозна­чения приведены выше).

Граничные условия для такой дифференциальной модели зо­ны дозирования имеют вид

При у = 0

При х = 0 и x = w (для всех у) .

(5.53)

Vz = Uz — U cos<p

Нри 0 < да и у = А

Где Ts и Ть — соответственно температуры червяка и стенки корпуса.

Итак, компоненты напряжений тХу и тух оказываются функ­циями только у и z, причем последняя зависимость возможна и в том случае, если T=T(z).

При записи уравнений энергетического баланса будем счи­тать, что теплопередача за счет теплопроводности вдоль оси канала пренебрежимо мала. В этом случае уравнение (5.52) сведется к виду

Рсрьг Тгу(5.54),

Представленное в такой форме уравнение (5.54), по сущест­ву, превращается в уравнение тепловыделения. При его интегри­ровании нужно учитывать температурные условия на поверхно­сти полимерной струи, имея в виду, что температура поверхно­сти зависит от теплообмена с окружающей средой.

Можно проинтегрировать (5.54) по у. В этом случае вместо дифференциального уравнения для элементарного объема полу­чим дифференциальное уравнение для элементарного сечения:

DT dW dP QpCp-^=K_ + Q — (5.55)

Где dW—мощность вязкого трения, рассеиваемая на участке длиной dz.

Для учета теплообмена с окружающей средой в уравнение (5.55) введена дополнительная характеристика процесса — ко­эффициент политропичности К, который характеризует направ­ление теплового потока и количество тепла, отводимого в окру­жающую среду или, наоборот, подводимого извне.