Оборудование заводов по переработке пластмасс

ГОЛОВКИ ЭКСТРУДЕРОВ. КОЭФФИЦИЕНТЫ СОПРОТИВЛЕНИЯ

Головка экструдера — это профилирующий инструмент, придаю­щий необходимую форму выдавливаемой струе полимера. От степени совершенства конструкции головки в значительной ме­ре зависит точность поперечных размеров экструдируемого из­делия и качество его поверхности. В соответствии с этим назна­чением конструкция головки должна удовлетворять следующим требованиям: 1) она должна способствовать формированию по­перечного сечения потока, соответствующего форме сечения экструдируемого изделия; 2) геометрические размеры профили­рующей щели и углы выхода должны обеспечивать возможность работы с максимальными значениями производительности, при которых еще не наблюдается «эластической турбулентности»; 3) конфигурация каналов должна исключать образование в них зон застоя; 4) головка должна обладать достаточным сопротив­лением, чтобы на выходе из червяка создавалось противодавле­ние, обеспечивающее качественное смешение и гомогенизацию полимера; 5) конструкция профилирующих органов должна быть достаточно жесткой, чтобы при любых рабочих давлениях сечение проточной части оставалось неизменным; 6) конструк­ция головки должна обеспечивать возможность регулирования распределения объемного расхода по периметру струи для устранения влияния неточностей расчета и изготовления на про­филь экструдируемого изделия.

Далеко не все эти задачи поддаются строгому количествен­ному анализу, н в настоящее время при проектировании голо­вок используется не только точный инженерный подход, но и в значительной мере колоссальный практический опыт, накоплен­ный в этой области.

Одна из основных проблем, которые приходится решать при конструировании головок, — это определение коэффициента со­противления, позволяющего рассчитать давление экструзии и определить фактическую производительность экструзионного аг­регата.

Объемная производительность определяется как решение си­стемы двух уравнений: описывающего внешнюю характеристику экструдера Q = Q(P)n при заданных условиях {N, Ты) и описы­вающего внешнюю характеристику головки Q = Q(Pt)t• Решение этих уравнений можно находить как численным, так и графиче­ским методом, нанося на один график обе характеристики (рис. 5.29). В этом случае точка пересечения кривых (точка А) и оп­ределяет величину фактической производительности. Эта точка называется рабочей точкой.

Следует отметить, что определение коэффициента сопротив­ления строго аналитическим методом даже в случае экструзии расплавов, обладающих свойствами ньютоновских жидкостей, возможно только в ограниченном числе простых случаев тече­ния. Необходимость учета аномалии вязкости в еще большей

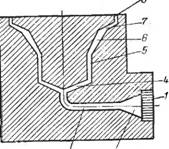
Рис. 5.30. Схема проточной части головки для получения пленки рукавным методом:

/ — цилиндрические каналы решетки; 2 — сходя­щийся конический канал; 3 — цилиндрический ка*' иал; 4 — разводящий канал; 5, 8 —кольцевой ци­линдрический канал; 6 — кольцевой конический расширяющийся канал; 7 — кольцевой конический сужающийся канал.

Мере сужает круг задач, поддаю­щихся строгому аналитическому подходу. Поэтому обычно прибега­ют к методам приближенного рас­чета, основанным на замене реаль­ных проточных систем упрощенными моделями, составленны­ми таким образом, чтобы каждый из элементов модели можно было свести к форме, поддающейся аналитическому описанию.

Рассмотрим в качестве примера схему головки для получе­ния пленки рукавным методом, схема которой изображена ни­же на рис. 5.43. Можно в первом приближении считать, что со­противление, которое преодолевает поток, проходящий через эту головку, эквивалентно сопротивлению, которым обладает си­стема из восьми каналов, изображенная на рис. 5.30.

При расчете суммарного коэффициента сопротивления будем исходить из очевидного условия, что полный перепад давле­ния в головке Рг, соответствующий некоторой заданной величи­не объемного расхода, складывается из перепадов давления, необходимых для преодоления сопротивления каждого из уча­стков канала в отдельности:

Т

Г=1

Где т — число отдельных участков.

В общем случае объемный расход через канал с неизменной геометрией зависит от перепада давлений следующим образом:

В случае моделирования свойств среды ньютоновской жидко­стью

Q = КГРГ/П (5.96)

В случае моделирования свойств среды аномально вязкой жидкостью

Q = KT'(P/v)n (5.97)

Где Кг и К/ — соответственно коэффициенты сопротивления при течении нью­тоновской и псевдопластичной («степенной») жидкостей.

Располагая значением коэффициента сопротивления для каж­дого из элементарных участков в отдельности, можно записать в случае моделирования расплава ньютоновской жидкостью:

АР; = Qm/Kri (5.98)

Рис. 5.31. Цилиндрический канал круглого сече­ния.

При этом выражение (5.98) позволяет учитывать изменения эффективной вязкости в разных участках канала, вызванные как различием в значениях градиента скорости, так и измене­нием температуры. Эффективная вязкость в пределах каждого участка рассчитывается по кривой течения при соответствующем значении пристенного градиента скорости.

Рассчитав значения эффективной вязкости и коэффициента сопротивления для каждого элемента канала, можно определить суммарный коэффициент сопротивления по формуле

І-ї-тсі •

111

1=1

Зная Кг?., можно определить давление в головке:

Рт = ФПі/^гЕ (5.100)

Где г)і — эффективная вязкость в канале профилирующей матрицы.

Если учет аномалии вязкости производится не введением эф­фективной вязкости, а непосредственно интегрированием урав­нений движения степенной жидкости, то суммарный коэффи­циент сопротивления определяется выражением

1/п

1= 1

Выражение (5.101) позволяет определять суммарный коэф­фициент сопротивления для всех случаев экструзии расплавов пластмасс. Единственное существующее при этом ограничение сводится к требованию, чтобы влияние температуры сказыва­лось только на значении константы р,;.

Определим коэффициент сопротивления и значение пристен­ной скорости сдвига yw для элементарных случаев течения.

Круглый цилиндрический канал (рис. 5.31). Используя метод эффективной вязкости, можно записать

Кг = л/?4/(8£) (5.102) yw = Q(n + 3)/(я/?3) (5.103)

Использование степенного закона дает

Кг' = я/?"+3/[2"(п + 3)L«] (5.104)

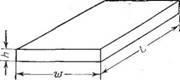
Плоский щелевой канал (рис. 5.32,с). Используяме - тод эффективной вязкости, получим:

Kr = wh4'p(h/w)/(2L) (5.105) VW = 6Q/(wfi2) (5.106)

Использование степенного закона дает:

Whn+2Fp (h/w) Kr - (п + 2) 2"+1 Ln ( '

' Коэффициент Fp(h/w), входящий в уравнения (5.105) и (5.107), учитывает тормозящее влияние стенок и определяется по номограмме, приведенной на рис. 5.25, или по формуле (5.64).

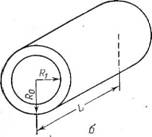
Кольцевой цилиндрический канал (рис. 5.32,б). Используя метод эффективной вязкости, имеем:

KF = n (R0 + Ri) (R0 — Rifl(2L) (5.108)

Yw= QQ/[n(R02 — Ri2) (R0—Ri)] (5.109)

Применяя степенной закон, получаем:

Кг' = я (R0 — Ri)^ (R0 + Ri)![(n + 2) 2«+і£«] (5.110)

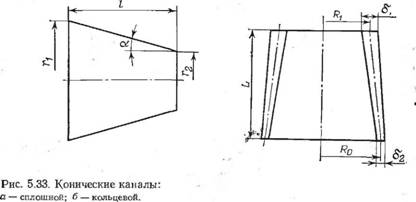
Конический канал (рис. 5.33, с). Используя метод эф­фективной вязкости, получим:

Я(1— cos и)2 (1+2 cos а) Лг— sin3 а (2 — 3 sin2 a) (r2~s — rx~a) (i>. ill)

V = 8Q IL (-A - + - Xr-)S

" ^ I L sin а ~ sin а ]

-Ступенчатая аппроксимация. Существует метод расчета ко­эффициента сопротивления конических каналов, основанный на использовании ступенчатой аппроксимации реального канала се­рией цилиндрических ступеней, длина которых выбирается та­ким образом, чтобы диаметры соседних ступеней отличались друг от друга не более чем на 10%.

Рис. 5.32. Щелевые каналы:

А~ плоский; б — кольцевой цилиндрический.

Конический канал. Используя уравнения (5.101) и (5.104) и принимая температуру постоянной по всей длине ка­нала, получим:

/ т -п

= 2"(и + 3)А1п (2 ) (5.113)

Где т — число ступеней, равное m=L/Al; АI — длина ступени;

= + (5-114)

Конический кольцевой канал (рис. 5.33, б). При­менив метод ступенчатой аппроксимации, выразим размеры эле­ментов ступени через размеры моделирующего канала. Из гео­метрических соображений следует:

R« = R1 + ±+ ^-Я'Н-^-Ц -- 1) (5.115)

= ЧЬ-Ы-Ь-и (і — 1) (5.116)

Используя (5.101) и (5.110) и принимая температуру по всей длине канала постоянной, получим:

1

2 '(Я0г - RuY^I" (R0 + Р^)1"1 J (5Л17)

Метод ступенчатой аппроксимации обычно дает хорошие ре­зультаты. Особенно удобно им пользоваться в тех случаях, ког­да вычисления производятся с применением ЭЦВМ.

5 6. ПРОИЗВОДИТЕЛЬНОСТЬ ЭКСТРУДЕРА. РАБОЧАЯ ТОЧКА. ОСНОВНЫЕ ПАРАМЕТРЫ ПРОЦЕССА

Изложенные в предыдущих разделах сведения позволяют рас­считать внешнюю характеристику экструдера и внешнюю харак­теристику головки независимо друг от друга. В действительно­сти всегда приходится иметь дело с их сочетанием. Поэтому фактический рабочий режим определяется как решение систе­мы двух трансцендентных уравнений, одно из которых описыва­ет внешнюю характеристику червяка Q = Q(P)N, а другое — внешнюю характеристику головки Q = Q(Pr)r■ Решение, одно­временно удовлетворяющее обоим уравнениям, называется ра­бочей точкой, поскольку при заданной скорости вращения чер­вяка производительность экструдера, так же как и температура и давление экструзии, определяется этим решением.

Использование описанной математической модели позволяет решить ряд практических задач, основными из которых являют­ся следующие: поверочный расчет экструдера; проектный расчет экструдера; анализ технологического режима, включающий ис­следование влияния вариаций температуры нагревателей корпу­са и свойств сырья на стабильность размеров и температуры экструдируемого изделия.