Оборудование заводов по переработке пластмасс
Физическая сущность процесса вальцевания
Рассмотрим движение полимера в зоне между двумя вращающимися валками (рис.
4.15). Вследствие прилипания наружный слой материала движется вместе с поверхностью валка. Из-за наличия сил внутреннего трения наружный слой увлекает прилегающие к нему слои, и вся масса материала начинает втягиваться в зазор.
|
|
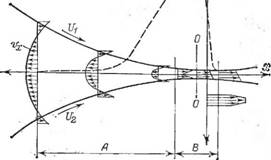
Поскольку площадь поперечного сечения зазора по мере удаления от входного сечения (поверхность А—А) все время уменьшается, а обрабатываемый материал практически несжимаем, скорости движения слоев материала, расположенных на разных расстояниях от поверхности валка, оказываются различными. Распределение скоростей в зазоре между валками для сечений, расположенных на различном расстоянии от входа в зазор, показано на рис. 4.16. Всю рабочую зону можно разделить на две области: область А, в пределах которой центральная часть потока движется в направлении, противоположном направлению движения валков, и область В, в которой весь находящийся в зазоре материал движется в одном направлении.
|
|
|
Р(х > / V
Рис. 4.16. Распределение скоростей и давлений в вальцуемом материале. |
|
|
При этом скорость движения материала по мере удаления от поверхности валка увеличивается.
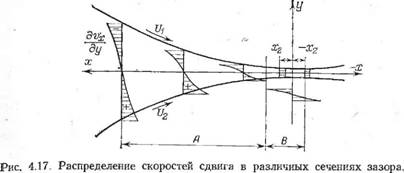
Существование переменной по сечению скорости приводит к возникновению в материале, транспортируемом через зазор^ деформации сдвига. При этом скорость деформации зависит как от окружной скорости, так и от размера зазора, увеличиваясь с возрастанием скорости и уменьшением зазора. Типичное распределение скоростей сдвига по длине зазора приведено на. рис. 4.17.
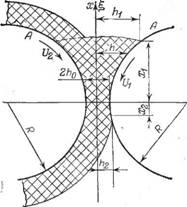
Поскольку скорость сдвига пропорциональна напряжению - сдвига, в разных точках находящегося в зазоре материала действуют различные напряжения сдвига, абсолютное значение и; направление которых меняются в зависимости от места расположения и режима (скорость, зазор, температура). Типичная', картина распределения напряжений в зазоре между валками, приведена на рис. 4.18.
Таким образом, материал, проходящий через зазор вальцов,. подвергается воздействию напряжений сдвига и претерпевает: существенные деформации сдвига. При этом материал, находящийся в области А (см. рис. 4.16), участвует как в поступательном, так и в циркуляционном движениях. Существование области циркуляционного течения и областей с различной ориентацией скорости сдвига и обусловливает возможность применения, вальцов для смешения.
Смешение происходит в зазоре вальцов за счет того, что. вальцуемый материал подвергается большим сдвиговым деформациям, которым сопутствует периодическая переориентация* расположения поверхностей раздела вследствие циркуляционного течения в области А и существования областей разноори - ентированных деформаций сдвига.
Для более эффективного смешения применяют вальцы с. фрикцией, наличие которой интенсифицирует циркуляционное течение в области А. Так как перемешивание материала происходит только в плоскости, нормальной к оси валков, для выравнивания продольного распределения концентраций смешивае-
|
Zfl |
|
Оа |
|
|
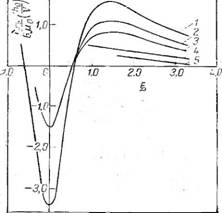
Рис. 4.18. Распределение напряжений сдвига в зазоре между валками; значения rj:
1 — 1: 2 — 0,8; 3 — 0,6: 4 — 0.4; 5 — 0,2.
Мых ингредиентов вальцуемый материал периодически снимается с поверхности валка, скручивается в рулон, который поворачивается на 90° и вновь пропускается в зазор между валками. Таким образом достигается переориентация областей, ранее располагавшихся в разных местах образующей валка, которые при
Этом оказываются расположенными примерно в плоскости одно - то нормального сечения. Поэтому дальнейшее вальцевание обеспечивает выравнивание концентраций в направлении, не охваченном в предыдущем цикле.
Возникновение в проходящем через зазор материале значительных напряжений сдвига позволяет кроме смешения осуществлять при вальцевании и операции диспергирования. Вследствие этого вальцевание используют не только для смешения, но и для диспергирования в полимере твердых и жидких ингредиентов (тальк, технический углерод, мел, пластификаторы, стабилизаторы, красители и т. д.). Поскольку процесс диспергирования происходит тем интенсивнее, чем выше напряжение сдвига, а величина напряжения сдвига, в свою очередь, однозначно определяется эффективной вязкостью, диспергирующее вальцевание следует вести при минимально возможных температурах, ггак как при этом вязкость, а следовательно, и напряжения сдвига максимальны.
Описанные выше изменения в характере течения материала, находящегося в зазоре, проявляются в изменении гидростатического давления. Типичная кривая распределения давления Р(х), полученная при экспериментальном исследовании процесса вальцевания, была приведена на рис. 4.16. Сопоставление аюля скоростей с эпюрой давлений показывает, что трансформация поля скоростей сопровождается увеличением давления, достигающего в какой-то точке максимума. Профиль скоростей в. этом сечении имеет вид, изображенный на рис. 4.16 (сече - ;ние О—О). Такая форма профиля скоростей показывает, что. силы, возникающие вследствие изменения гидростатического давления и действующие с одной стороны сечения, полностью уравновешиваются аналогичными силами, действующими с другой стороны. Следовательно, напряжение сдвига в этом сечении равно нулю, и материал движется подобно твердой пробке, не
подвергаясь никаким деформациям сдвига. При дальнейшем' движении материала это равновесие нарушается, и центральные - слои начинают двигаться с большей. скоростью, чем слои, прилегающие к поверхности валков. Максимальная разница достигается в минимальном сечении, расположенном на линии, соединяющей центры валков. Дальнейшее движение сопровождается: торможением центральных слоев. Наконец, на выходе из зазора избыточное давление падает до нуля, а профиль скоростей вновь, принимает прямоугольную или трапециевидную форму.
4.4.2.2. Гидродинамическая теория изотермического вальцевания полимеров, обладающих свойствами ньютоновской жидкости
Для вывода Основных уравнений теории изотермического вальцевания рассмотрим схему движения, приведенную на рис. 4.15.
Дифференциальные уравнения движения материала записываем в форме уравнения Стокса без учета массовых сил (считаем, что жидкость несжимаема, траектории частиц материала мало отличаются от параллельных, квадратичными членами инерции пренебрегаем):
|
Дх дР |
|
(4.15а) |
|
Ду |
ДР і d2vx d2vx
|
/ о vy o'vr
|
Пренебрегая сжимаемостью расплава, запишем уравнение неразрывности - в виде
|
Дх ду |
Dvx dvy
= 0 (4.16>
Принимая, что материал прилипает к поверхности валков, сформулируем; граничные условия:
Vx I = U cos [arcsin (x/R)] = U УI — x2/R2 ~ U (4.17>
y=h
P (*i) = P (—= 0 (4.17a>
Далее, полагая, что члены вида dvx/dx и dvy/dx пренебрежимо малы, и принимая, что дР/дх^дР/ду, сведем уравнение (4.15) к форме, аналогичной, уравнению Рейнольдса:
DP * ,А IRV
Сделанные допущения справедливы в том случае, если h0 мало по сравнению с R, а вязкость среды [і столь велика, что инерционными и массовыми силами можно пренебречь (число Рейнольдса мало).
Интегрируя уравнение (4.18), получим
В случае движения материала в зазор между валками, вращающимися с одинаковой окружной скоростью (Ui = U2), задача становится осесимметрич - ной. Следовательно, dvJdy^O при у= 0, отсюда Сі = 0. При наличии фрикции - нулевое сечение смещается в сторону валка, вращающегося с меньшей ско
ростью. При этом величина Сг оказывается равной
Сг = ~(U0/h) к (4.20) тде (У0= (Ui+U2)/2 — средняя окружная скорость валков;
X=(U1-U2)/(2U0) (4.20а)
Интегрируя уравнение (4.19), получим для случая Я=0:
|
2(х dx |
Ф dP
+ С2 (4.21)
Если ^=5^0, то
DP у2 иЧм
Постоянные интегрирования определим из условий прилипания (4.17), аюлагая, что x/R<^ 1. Следовательно, vx{h) = 11 и ид—h) = U2.
В случае 7І=0 имеем:
H dP
Тогда выражение для vx принимает вид
Обратим внимание, что в уравнении (4.22) течение в зазоре между вал» жами представлено как сумма двух потоков: один поток—-это течение с прямоугольным распределением скоростей (вальцуемый материал движется, как твердое тело, со скоростью, равной окружной скорости валков); второй поток — это течение под давлением, направление которого зависит от знака градиента давлений. На участке зазора, в пределах которого градиент давлений положителен, второй поток направлен навстречу основному движению материала. В результате в центральной части зазора возникает область противотока и, как следствие этого, — циркуляционное течение.
При наличии фрикции (Х^=0) постоянная интегрирования, определенная из условий прилипания, равна
H2 dP
Подставляя это выражение в уравнение (4.21а), получим:
„_-„.(,t^-Jf^-i - (..Ш)
Выражение для vx оказывается совершенно аналогичным уравнению (4.22), отличаясь от него только тем, что вместо постоянной окружной скорости U в него входит произведение среднего значения скорости на безразмерный параметр І+гД/ft.
Величина h (расстояние от оси симметрии зазора до поверхности валков) -связана с координатой х соотношением
H = h0 + R — yR* — x* (4.23)
Объемный расход через единицу ширины зазора определяется выражением
H
(4-24)
При отсутствии фрикции интегрирование этого уравнения дает следующее выражение:
/ h? dP ,, „, г
При! наличии фрикции величина объемного расхода равна
|
( |
/j2 dP
И°х — "3jT ~dx) <4-24б>
Введем безразмерные переменные:
І = х/УШЇ0; Г] = y/h (4.25)
Соответственно получим:
Si = ^/УШо, |2 = (4.26)
Далее, разложим стоящий в правой части выражения (4.23) корень квадратный в биномиальный ряд и ограничимся первыми двумя членами ряда:
Л=М 1+£2) (4-27)
Заменяя градиент давлений dP/dx в уравнении (4.24) на
DP dl __ dP______ l_
Dl dx dg УЩ,
И подставляя h из (4.27), получим:
DP SfiU! f2R
1 / IK
У ИГ (4-28)
Dl - к (і +12)3 V к
Входящий в уравнение (4.28) параметр определяется из условия dP/dx=0 при х=х2'
= yQ/(2Uhn) - 1 (4.29)
С другой стороны, величина £2 определена выражением (4.26).
Следовательно, между объемным расходом и координатой точки отрыва вальцуемого материала от поверхности валка существует однозначная связь:
Х, = y2Rh0 Q/(2Uh0) — 1] (4. ЗО)
Для вальцов с фрикцией величина продольного градиента давлений определяется выражением, аналогичным (4.28):
DP 3(а£/„ лГЖ оя
Соответственно изменится и соотношение для определения |2:
^=У(3/(2ВД - 1 (4.29а)
Интегрируя уравнение (4.28а), получим выражение, описывающее распределение давлений в зазоре:
= + . (4.31)
Функция g"(|2, определяется уравнением
£ fe, і) = g ~(1 - arctg 1 (4 ■з2)
|
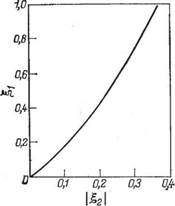
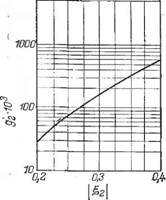
Рис. 4.19. Зависимость |і от | 1 - Рис. 4.20. График зависимости g2 от ||2|. |
Постоянная интегрирования С определяется из граничного условия
Р(-Ы= 0:
|
(4.33) |
|
С=- |
|
1+1 |
|
(4.36a) |
|
Vx = - U |
|
Зі!2 (I2 — І22) + 3|22 — I2 + 2 2(1+12) |
|
Типичная картина распределения скоростей, рассчитанная из уравнения (4.36), приведена на рнс. 4.16. Заметим, что при |= ±|2 правая часть уравнения (4.36а) не зависит от т]. Это означает, что при отсутствии фрикции ма- |
1 + 3|22
,1-0-3^) arctg 1|
Приравнивая производную dP/d% нулю, получим, что при |=+£г функция Р( 1) проходит через максимум.
Далее обратимся к уравнению (4.31). Поскольку по условию (4.17а) Р(£і) =Р(—4г) =0, выражение (4.32) должно иметь два корня, при которых оно обращается в нуль. При этом, поскольку один из них определяется выражением (4.29), второй определяется условием
*(Ь. Е.> = - С(Е2)«-бБ,8 • 34)
Следовательно, между gi и |-|2| существует однозначная функциональная зависимость, график которой приведен на рис. 4.19. Можно с достаточно высокой точностью аппроксимировать эту кривую зависимостью
/ 0,33
B = -*('.g+o. B5-iu) <4-35>
Распределение скоростей. Чтобы получить выражение, описывающее распределение скоростей в зазоре между валками, воспользуемся соотношением (4.22а), произведя в нем замену переменных (х на g и у на т]) и подставив в него значение dPjd% из уравнения (4.28а):
»*= - T+fT [4V № - + + Ф (1 + I2)] (4.36)
|
|
В случае вальцевания без фрикции Я=0 уравнение (4.36) переходит в известное уравнение:
Териал в этих сечениях движется с постоянной скоростью. Если же скорость вращения неодинакова, то в этих сечениях эпюра скоростей имеет форму трапеции, поскольку по мере удаления от оси симметрии скорость линейно увеличивается (или уменьшается — в зависимости от знака г]) в соответствии с последним членом выражения (4.36).
Объемный расход через единицу ширины зазора определяется интегрированием выражения для vx в пределах от —h до +/г. Наиболее рационально выполнить это интегрирование в сечении, в котором І=+Із. Тогда в случае вальцевания без фрикции
1
Q = 2h j = 2 Uh0 (1 + I*) (4.37)
О
В случае вальцевания с фрикцией
_Q=2t/0/i0(l+Ј22) (4.37а)
Выше отмечалось, что на входе в зазор существует область циркуляционного течения. Границу этой области можно определить, положив vx=0 при т]=0. Величина граничного значения |s определится как корень квадратного уравнения
—is2 + 3|2а + 2 = 0 (4.38)
Т. е.
Is = l/3l? T2 (4.38а)
Поскольку вся зона противотока расположена в области положительных значений отрицательный корень отбрасываем.
Скорость сдвига в зазоре можно определить, дифференцируя уравнение (4.36а):
___ U0 Зт1(|2-£22) + М1+Г)
Ду - дц ду - h0 (1+g2)2 (4'dy)
Распределение давлений в зазоре описывается выражением (4.31). Для приближенного учета аномалии вязкости подставим в это выражение вместо постоянной вязкости эффективную вязкость. Положив средний
Градиент скорости y=Uo/ho, получим:
Р ®=/®+(4-40)
Существование аномалии вязкости приводит к ослаблению зависимости давления от скорости вращения и величины зазора, тем большему, чем больше индекс течения.
Определим максимальное давление, полагая в выражении (4.40) |=+12:
|
Здесь |
Ш ' 7^6.» (4-41)
Распорное усилие, приходящееся на единицу ширины валка, определим, интегрируя уравнение (4.40):
— г 3и R / U
Т = 1/2Rh0 ) Р (|) dl = g2 (Јs) (4.42)
Її
G2(l2) = 'i+IJ1 Ei + 1Ы +5|І2і3(1+Іі2)] +
|
IVV^ Г _R_ Hi in у 2hg |
+ (1 - 3|22) dial arctg 112 I - Ь arctg |г) (4.43)
Номограмма зависимости g2 от ||2| представлена на рис. 4.20. С увеличением ||2| значение функции £г( |Ы) довольно быстро растет. Так, при изменении |2 от 0,2 до 0,3 значение ^(ІІгІ) возрастает почти в 5 раз. Это указывает на существенную связь между объемом загрузки и распорным усилием. Поэтому во избежание поломки вальцов никогда ие следует сразу загружать на валки всю порцию вальцуемого материала. Напротив, необходимо 'загружать' материал постепенно, с тем чтобы величина росла вместе с увеличением температуры вальцуемого материала. Тогда увеличение распорного усилия, вызванное ростом значения функции Ё2{Ы), будет компенсироваться уменьшением эффективной вязкости вследствие разогрева материала.
Аномалия вязкости приводит к значительному уменьшению распорных усилий [см. уравнение (4.42)]. Для иллюстрации определим отношение распорного усилия Гц, рассчитанного по формулам ньютоновского течения, к распорному усилию Тіа, рассчитанному с приближенным учетом аномалии в случае вальцевания расплава, для которого [х0= 10~3 МПа-с1/2, а п=2 (при расчете в ньютоновском приближении принимаем, что u, n= 10—3 МПа-с; U/h„^ «250 с-'):
ТЪа №)1/П 1 V
Иначе говоря, распорное усилие, рассчитанное без учета аномалии вязкости, оказывается примерно в 15 раз больше, чем распорное усилие, рассчитанное с учетом аномалии вязкости.
Из уравнения (4.43) видно, что распорное усилие очень сильно зависит от расстояния между валками, увеличиваясь с его уменьшением. Это связано с тем, что при уменьшении /іо одновременно увеличивается |2 и, следовательно. 82(^2) и возрастает множитель x0(U/ho)lln, поскольку ho входит в знаменатель. Экспериментально показано, что при уменьшении в 4 раза толщины (калибра) каландруемой пленки (от 0,1 до 0,025 мм) распорное усилие возросло в 4,8 раза (материал — наполненная композиция на основе поливинил - хлорида). Казалось бы, аналогичное влияние на распорное усилие должна оказывать и скорость вращения валков. В действительности этого не происходит, потому что одновременно с увеличением скорости вращения валков возрастает интенсивность тепловыделения, что приводит к снижению вязкости.