Оборудование заводов по переработке пластмасс
Экспериментальная оценка гомогенности смеси
Для статистической оценки качества смеси от нее отбирают ряд одинаковых проб (не менее десяти), объем которых должен превышать объем предельной частицы по меньшей мере в 103 раз. Очевидно, что даже в идеальной смеси число частиц ДФ в разных пробах будет различно.
Статистическая теория смешения предсказывает, что распределение числа частиц ДФ в отобранных пробах должно подчиняться биномиальному закону:
Р(*)= Ь (п— Ь) (4.1)
Где х=Ь/п — предполагаемое относительное содержание ДФ в пробе (Ъ — предполагаемое число частиц ДФ в пробе, п — общее число предельных частиц в пробе); q — относительное содержание ДФ в смеси.
|
(4.2) |
Для такой идеальной смеси мерой предельной неоднородности, неизбежна Даже в идеальной смеси, является генеральная дисперсия (ГД) а2:
A* = q(-q)!n
Формула (4.2) позволяет вычислить относительную ГД. Для определения фактической ГД — Сф2 — необходимо умножить результат на п2 и д2:
Cii? = q*(l-q)n (4.2а)
Минимальный размер пробы, которую можно считать представительной, должен удовлетворять следующему условию:
«мин >9/1(1-9) 9] (4.3)
В этом случае биномиальное распределение практически совпадает с нормальным (гауссовым) распределением, и для определения его характеристик можно пользоваться обычным аппаратом математической статистики.
На практике для оценки гомогенности смеси необходимо проанализировать отобранные пробы и определить, соответствует ли распределение концентрации ДФ в пробах закону биномиального распределения.
Существует много способов определения качества смешения. Наиболее рациональны те из них, которые основаны на сопоставлении ГД и экспериментальной дисперсии (ЭД) диспергируемой фазы. Для этого данные, полученные при анализе отобранных проб, используют для определения средней концентрации х и экспериментальной дисперсии ДФ s2 в пробах:
J N. / N
*=лг2*г (44) 52=ЖГТ <4-4а>
І=і г=і 1
Где N — число параллельных проб; xt — концентрация ДФ в і-й пробе.
При этом величина х не должна сильно отличаться от q—• относительной концентрации ДФ в смеси. Если х сильно отличается от q, то выбранное число проб явно недостаточно для оценки качества смеси.
|
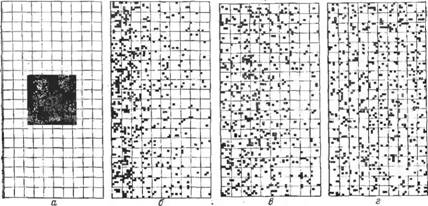
Рис. 4.1. Модельные смеси с разной степенью однородности. Пояснения в тексте. |
Наиболее распространенный критерий смешения — это индекс смешения 1\
/1=a2/s2 (4.5)
Индекс смешения изменяется в интервале от 0 до 1. Значение /1 = 0 соответствует совершенно несмешанной системе. При Ii = система обладает свойствами идеальной смеси. Иногда применяется в качестве критерия однородности критерий Лейси-
H= K2-ss)/(°o2-oa) (4.6)
Где Coz=9(l— Q)—дисперсия исходной системы, вычисленная в предложении и=1.
Значение /2 также изменяется от 0 (совершенно несмешанная система) до 1 (идеальная смесь).
Для оценки качества смеси можно также использовать коэффициент вариации v (%):
V = (s/x) ■ 100 (4.7)
У хороших смесей значение коэффициента вариации составляет доли процента.