Моделирование миграции подземных вод
Растворение и осаждение
Растворение и осаждение — два взаимосвязанных и взаимообусловленных процесса, влияющие на состав подземных вод и их использование. Например, освоение геотермальной энергии подземных вод в теплоэнергетике в значительной мере ограничено образованием труднорастворимых осадков в системах транспорта воды в поверхностных условиях. В результате нестабильности подземных вод качественно меняется химический состав — макрокомпо - нентный за счет образования основной массы осадка и микрокомпонентный вследствие соосаждения и сорбции осадком микроэлементов, Геологическая и геохимическая роль процессов осаждения наиболее очевидна, например, в образовании специфических осадков в местах естественной разгрузки подземных вод (карбонатные травертины, гейзериты, натечные формы карбонатов в пещерах, гипсовая и карбонатная цементация песчаных отложений, трубчатые формы отложений сульфидных минералов).
К геологическим проявлениям растворения следует, отнести •формирование карста в карбонатных и сульфатных породах. Довольно часто на земной поверхности и при каптаже подземных вод отмечаются гидроксиды железа (III). Для процессов смешения сероводородных подземных вод с железосодержащими характерно •образование сульфидов железа (гидротроилит FeS-ftH20), а когда железо в водах отсутствует, формируется серовато-Желтый осадок элементарной серы. В тех случаях, когда подземные вОды в условиях пласта насыщены легкорастворимыми солями, последние при подъеме на поверхность способны отлагаться из воды, образуя соляные пробки на устье скважин.
Однако, как бы ни были разнообразны геологические и геохимические следствия деятельности подземных вод, в их основе лежат физико-химические законы и термодинамические уравнения равновесия.
В качестве примера термодинамического описания процессов растворения и осаждения рассмотрим реакцию растворения труднорастворимого вещества типа МегХу [3]:
МекХ3,(пі?:гМеУ++уХ*-.
По закону действующих масс с учетом того, что активность твердой фазы постоянного состава равна 1, запишем уравнение константы равновесия этой реакции:
[Меу^]г[хг']у = к^ь (3.9)
Где /Ств — константа произведения растворимости, или сокращенно произведение растворимости. С учетом условий материального баланса по катиону [Ме^] =zS и аниону произведение растворимости имеет вид
(3.10)
Где S — растворимость труднорастворимого соединения, моль/л.
Выражения (3.9) и (3.10) можно использовать только для ориентировочной оценки растворимости солей, так как в них не учитываются образование комплексных ионов и величина коэффициентов активности.
Особенно велики погрешности, если речь идет о соединениях, обладающих относительно высокой растворимостью, например о гипсе, у которого ионная сила насыщенного раствора (S=1,50X ХЮ~2) составляет 0,04 и требует введения существенных поправок на неидеальность системы. Как будет показано ниже, даже в чистой воде треть величины растворимости гипса составляет комплексная частица CaS04°.
Для относительно простых соединений типа CaS04 или BaSO* ориентировочный расчет по величине произведения растворимости ведется ПО формуле 52 — ^BaSO,
Для более сложных соединений, например CaF-г, уравнения материального баланса имеют вид S—[Са2+] и 2S=[F~], а растворимость определяется согласно выражению 4S3 —КСйР .
Учет реального взаимодействия даже в простых системах резко усложняет расчетные зависимости и обычно приводит к уравнениям значительно более высоких порядков. В простейшем случае при расчетах растворимости можно ограничиться использованием величин коэффициентов "активности, учитывающих различные виды взаимодействия в системе. Например, если в растворе бьіліг аналитически определены ионы Са2+ и S042-, то уравнение произведения растворимости может быть записано в виде
WsO»" fCa2+J tS0M = ^eaSO, '
Если при данной ионной силе воды и определенных величинах коэффициентов активности (для удобства' используют выражение 2 ____________
Tcaso, — Tca2+Ts02- левая часть уравнения больше (или меньше) величины константы, то уравнение решается введением в материальный баланс искомой величины растворимости х:
7c. so4<lCa*1 +*)([SO»-] +*)=ATCaS04. (3.12)
В этом случае расчет сводится к решению квадратного уравнения, относительно величины х, причем отрицательные решения отбрасываются, а из положительных физический смысл имеет лишь одно значение.
Любая добавка общих ионов согласно уравнению произведения растворимости резко сказывается па равновесие системы, уменьшая растворимость соли. 48
Для примера оценим растворимость гипса в растворе, содержащем 0,1 моль/л СаС12. Условия материального баланса в этом случае имеют вид: [Са2+] =х+0,1 и [S042-]— х. По уравнению (3.12) без учета коэффициентов активности и при константе равновесия К= 10_48! получим квадратное уравнение ж(ж+0,1) — Ю-4-61, из которого находим х=2,46-10~4.
Содержание частиц CaS04° можно определить из соотношения констант равновесия реакций CaS04 Са»+ + SO2" и CaSO^ Са2+ - f SOj' как
<тв) Кг к2
Кі 10~4'S1
Rr gQno = =------------------------------ = 5,0Ы0-з.
XCaS04 ^ j q—2,31
Искомая величина растворимости гипса в первом приближении составит S— = 2,46-10~4+5,0Ы0_3=5,26-Ю-3, а ионная сила такого раствора будет /= = 0,1-3+2,46-10~4-4~0,30.
Из уравнения Дэвиса (2.4) определим величину коэффициентов активности ионов Y':
LgTi = 0.509.z] _ 0,2/J = 0,598 или ї(,а2+ = = 0,252.
Для ассоциата
CaS°4fgTCaSOo = 0,b/ ИЛИ ТСа5оГП07.
4 4
Введение коэффициентов активности в уравнение произведения растворимости (3.11) изменит его вид: х2+0,1 jc— 10-3'41 = 0 и даст новое значение растворимости, составляющей в расчете на ионы 3,72-Ю-3. Содержание ассоциата CaS04° после учета коэффициента активности будет определяться по уравнению
К IQ—4,61
*CaS04 = = = 4'68'10 •
4
В итоге растворимость гипса в 0,1 М СаС12 составит S=3,72- Ю-3 4- + 4,68-10_3=8,40-Ю-3 моль/л. Дальнейшее введение поправок на изменение ионной силы, а следовательно, и коэффициенты активности, нецелесообразно» так как изменение ее составляет всего десятые доли процента: /=0,3+1,49Х Х10-2~0,31. Полученный результат определения растворимости на 5% ниже экспериментально определенной величины (8,80-Ю-3 моль/л).
С увеличением концентрации электролитов погрешности таких расчетов обычно растут. Усложнение состава системы при наличии других электролитов требует учета в величине растворимости частиц типа NaS04~, MgSO40, СаНС03+ и др. О значении возможной погрешности в связи с комплексообразованием можно судить по приведенному выше примеру, где содержание CaS04° определяет более половины величины растворимости.
- В связи с этим в практических целях термодинамические расчеты процессов растворения и осаждения обычно ограничивают ионной силой подземных вод в пределах применимости уравнений Дебая — Хюккеля для коэффициентов активности (0,1 моль/л), что обычно соответствует минерализации подземных вод До 5 г/л. В более минерализованных водах прогнозная оценка процессов раствррения и осаждения возможна, но достоверность таких расчетов невелика. В случае относительно простых систем (например, хлоридных) обычно вводят в уравнения произведения раство
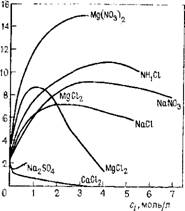
римости эмпирические параметры (например, коэффициенты активности той или иной соли, определенные по опытным данным). В случае смешения подземных вод, резко отличающихся по минерализации (пресных и рассолов), увеличение растворимости объясняется максимумом на изотерме растворимости гипса в растворе хлорида натрия (рис. 4). Появление общих ионов в этой системе, например, вследствие добавления хлорида кальция, более чем на порядок снижает растворимость. Присутствие сильных электролитов также сказывается на растворимости труднорастворимого карбоната кальция, однако это влияние несущественно в сравнении с действием растворенной углекислоты. Любая потеря углекислоты вследствие дегазации вод ведет к осаждению карбоната кальция в трубах, в местах выхода источников, на запорной арматуре скважин.
|
•■Са504,г/л
Рис. 4. Графики зависимости растворимости гипса от концентра - .ции различных электролитов (по В. В. Витвицкому) |
С ростом температуры растворимость большинства солей возрастает, однако эта зависимость часто неоднозначна. Для гипса увеличение растворимости ограничено 42 °С, а при более высокой температуре стабильной фазой становится другая кристаллическая модификация сульфата кальция (ангидрит), обладающая более низкой растворимостью. При температурах около 100 °С гипс дегидратируется с образованием метастабильных полугидратов CaS04-0,5 Н20. Для карбоната кальция повышение температуры приводит к снижению растворимости углекислого газа, а следовательно, к возможному выпадению избытка карбонатов в осадок. Характер изменения растворимости некоторых минералов в зависимости от температуры приведен в табл. 5.
|
Таблица 5 Растворимость некоторых минералов в воде [67] Растворимость минералов, г/л
|
|
Таблица б Растворимость минералов S в воде при 25 °С, давлении 105 Па и рН 7
|
|
* Значения получены прн парциоиаль'ном давлении рс0а, равном 100 Па и 104 Па - соответственно. |
Примеры реакций растворения некоторых солей в воде и их растворимость приведены в табл. 6.
С ростом давления растворимость большинства солей возрастает. В табл. 7 приведены данные, показывающие увеличение растворимости гипса.
При растворении оксидов и гидроксидов, электролитически диссоциирующих в воде, становится особенно отчетливой зависимость растворимости от значения рН.
Рассмотрим, например, такой процесс: Fe(OH)24*Fe2+-|-2PH-, для которого - при известных значениях химических констант получается lgFe2+=—14,7—
|
Таблица 7 Влияние давления на растворимость гипса (по данным С. Ф. Люшина, А. М. Ершова, Ф. А. Гарипова И Г. В. Галеевой, 1973)
|
|
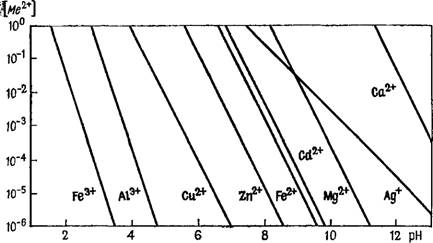
Рис. 5. Графики зависимости равновесного содержания ионов металлов от рН водного раствора |
—2(14)—2рН=13,3--2рН. Отсюда следует, что если величина рН изменяется от 8 до 7, то Fe2+ увеличивается от 2 до 200 ммоль/л.
На рис. 5 для некоторых металлов дано графическое изображение зависимости их растворимости от рН, причем видно, что с увеличением кислотности значительно возрастает миграционная мобильность ионов металлов (особенно тяжелых) в подземных водах.
При осаждении оксидов и гидроксидов путем адсорбции и ионного обмена на поверхности микрофлокуляции (в особенности тяжелых металлов Си, Со, Ni, Pb, Zn) этот процесс называется совместным осаждением.
Нередко определяющее значение для состава подземных вод имеет растворимость газов. Между количеством растворенного в воде газа Хі и его парциальным давлением над раствором рг существует равновесие, описываемое уравнением
*,=tfr/r = tfr? rTr. (3.13)
Где Кг — константа Генри; /г и - уг — летучесть и коэффициент летучести газа при данных р и Т [25].
Для чистой воды величина уг может быть принята за 1, и тогда уравнение (3.13) явится математическим выражением закона Генри— Дальтона: Хі = Кгрг-
В подземных водах высокой минерализации растворимость газов (неэлектролитов) как правило меньше, чем в чистой воде (явление высаливания). Уменьшение растворимости в зависимости от ионной силы воды описывается уравнением Сеченова [25] lg (x/x0) = KJ, где х—растворимость газа в чистой воде; л'0 — то же, в растворе с ионной силой I; Кс — коэффициент Сеченова (при 52
|
Таблица 8 Растворимость составляющих воздуха в воде Растворимость (в мг/л) при различной температуре (в °С)
|
25 °С для NaCl он равен ОД05, для MgS04 —0,066, для Na2SC>4 — 0,101).
Сравнительная оценка растворимости газов (см. ниже) и главных составляющих воздуха в воде (табл. 8) показывает, как велика потенциальная растворяющая способность подземных вод в отношении углекислоты и сероводорода. Растворимость некоторых газов в воде при парциальном давлении 105 Па и 0 °С:
Газ. . . Не Н3 N2 03 СН4 NH3 СО, H3S Растворимость, мг/кг 1,7 1,92 28,8 69,5 39,6 1000 3346 7100
Растворимость (в мг/л) в воде таких неэлектролитов, как нефть и нефтепродукты, невелика: для топливной нефти 10—50, бензина ~60, керосина 0,1—5. Нефтепродукты, попадая в поверхностные воды, распределяются следующим образом: на дне водоема оседает 40 %, в воде в виде эмульсии остается 40 % и на поверхности в виде пленки остается 20 %.
Если термодинамическое равновесие отсутствует, то согласно уравнению (3.3) получим соотношение
При индексе насыщенности /н> 1 раствор содержит избыток растворенных ионов, и происходит их осаждение, а при і„<1 продолжается растворение. Величина 1—/н часто используется в качестве показателя движущей силы процессов растворения и осаждения, причем, следуя уравнению кинетики химических процессов первого порядка, можно записать для скоростей растворения vp и осаждения vQ выражения [И]: ир=/Ср(1—/н); vQ — ~Ко(1н—1), где Кр и k0 — коэффициенты растворения и осаждения.
При построении расчетных моделей кинетики процессов растворения и осаждения целесообразно выделять два характерных случая, отражающих особенности взаимодействия фильтрующегося раствора со средне - и труднорастворимыми минералами породы. '
Скорость растворения среднерастворимых соединений, дающйГх растворы близкого к ним состава, в значительной степени лимитируется диффузионным механизмом межфазового взаимодействия. В соответствии с феноменологической концепцией Нернста, интенсивность такого рода процессов пропорциональна текущей суммарной концентрации веществ в растворе с и контролируется концентрацией насыщения с„ [7, 11]:
DNldt = ap(c-cB), (3.14>
Где ар — константа скорости гетерогенной реакции. При растворении твердой фазы c<.cH(dN/dt<.0), а при выпадении компонентов в осадок c>c„(dN/dt>0). Предполагая, что fc ходе процесса не меняется доступность растворяемого вещества водному раствору, Н. Н. Веригин принимает ар~М, где |=1 и |=0,5 соответственно при пластовом и дисперсном залегании растворяемого вещества [7]. Однако в реальных породах в процессе растворения (выщелачивания) вероятна метаморфизация пород, приводящая к усложнению уравнения растворения.
Дело в том, что процессы растворения (чаще их относят к разряду выщелачивания) труднорастворимых веществ, как правило, сколько-нибудь активно протекают лишь при взаимодействии с породой сложных растворов, содержащих несколько активных ингредиентов (причем часто одним из них является, растворенный газ). Это требует отражения в расчетных схемах миграционного процесса химических взаимодействий в явном виде через парциальные концентрации реагирующих веществ Сі с учетом стехио- метрических коэффициентов Vi конкретных реакций [71].
Пусть реакций растворения протекает по достаточно общей схеме: v^j + . . . + Vі* + - р. . . + гДе
А — содержание компонента. Тогда скорость изменения концентраций реагирующих веществ и продуктов реакции растворения в жидкой фазе Wsi в простейшем случае определяется выражением k
= П сл / —1, . . k, А+ 2, . . ., (3.15)
Где vi<0 для i>k-{-1; к— число компонентов, превращающихся в продукты реакции (&-И—твердое соединение); к* — общее число соединений, участвующих в реакциях.