Моделирование миграции подземных вод

Рациональные алгоритмы для численного моделирования конвективно-диффузионного переноса

Линейный поток. В линейном потоке теоретическая модель конвек­тивно-диффузионного переноса при распаде со скоростью %с и дей­ствии источников-стоков интенсивностью w представляется урав­нением

Дс D д2с v дс \ . w АЧ

----- —--------------------------------------- —• (7.9)

Dt п() дх2 п0 дх п0 «і

Из большего числа алгоритмов, используемых для рациональ­ного решения, может быть представлен алгоритм, основанный на конечно-разностной аппроксимации третьего порядка по времени О (Л/3), конечно-разностной аппроксимации второго порядка по про­странству О (Л*2) и вычислении суммарной функции источников стоков по правилу Симпсона. Для большей наглядности этот алго­ритм приводится при постоянных в пространстве и во времени па­раметрах и при постоянном пространственном и временном шаге дискретизации.

Временная дискретизация осуществляется на основе уравнения (7.8) путем замены в нем выражения dc/dt через правую часть уравнения (7.9), учитывая при этом, что d2c/dt2& (v/n0)2(d2c/dx2) [см. уравнение (7.4)]. В результате для уравнения (7.9) получает­ся следующая дискретизированная по времени форма:

М Г/гч v2bt\ дч дс, . яя;ч+ы „ лі, АІ.

----- D--------------------------- V----------- Хс 4- W — ПоС*+а( 4-

2 [\ 6п0 J дх2 дх J

I kt Г/гч, V2 ДА д2с дс, . 1' . , п /-7 1А\

+ — £> + -— — - V-------------------------- IC + W + П0С(=0. (7.10)

2 [V 6п0 J дх2 дх

Представив пространственные производные с помощью простой конечно-разностной аппроксимации второго порядка 0(Дл:2)

Дс/дх |„ ж (с„+1 - с„_і)/2д-*>

Д2фх21„ « (сп+і - 2сп + сп_,)!Ъх\

И представляя при w, независимости от с, суммарную функцию ис­токов s = Xc±nQc w уравнением s= (s„_[+4sra + sn+1)/6, получим

Дискретизированное в пространстве и во времени дифференциаль­ное уравнение (7.9) для п-й ячейки сетки

- -+- -

Введем для упрощения следующие обозначения: V D = D Д^/Дл;2; RN = (я0 + X Д*/2)/6; DZ = w Д

#0 = (я0 —X Д£/2)/6; DN = D — 1>2/(6я0); DO = D + <я2/(6я0) и получим уравнение

~-DN(cn+i-2сп + сп^у+*' + ^-(сп+1 - cn_xy+*<+RN(cn+l + + 4с„ + = /?0 (ся+1 + 4с„ + +jDO (<?я+1 - 2с„ +

+ £„-,)< (ся+, - с^У + DZ. (7.11)

4

Оно представляет собой п-е уравнение трехдиагональной систе­мы с неизвестными Xt = с1+&* и коэффициентами главной диа­гонали матрицы DN2 и вспомогательных диагоналей BN и EN, соответственно:

BNnXn_x + DN2nXn + ENnXn+i = Fn, где

Fn = BOnc\_x + D2nc<n + ЕОпс'п+1 + DZ„.

Для рассмотренного случая с постоянными параметрами имеем:

BN = — 0,5DN - 0,25V-j-RN; EN = — 0,50^ + 0,251/ + /?ЛГ;

Z)iV2 = + DN + 4W; BO = 0,500 + 0,25 V + RO\

EO - 0.5/Ю - 0,25 V 4- #0; D2 = - DO + 4/?0.

Одномерный поток переменного сечения. Процесс переноса в потоке (трубке тока) переменного сечения описывается уравне­нием

Е — = —(DA —) — Q —------------------ Lc ^W, (7.12)

Dt дх \ дх J дх

Где E—n0mB\ x — координата оси трубки тока; DA=Dmb\ Q — расход потока; L=Xmb\ W=wmb, m и b — соответственно мощ­ность и ширина потока в ленте тока. 126

Уравнение (7.12) при временной дискретизации, аналогичной для (7.10), может быть приведено к виду

[djc \ 6 / дх дх

\ 6 / дх дх

С пространственными производными, задаваемыми в соответствии с прил. 3.

Для суммарной функции источников-стоков в соответствии с правилом Симпсона имеем

„ ХП — хп-% $п-1 "Ъ, хпМ — хп 2 Sn - f - Sn+1

Хп+J — 3 xn+l — хп-1 3

При этом могут быть записаны уравнения, соответствующие урав­нению (7.11). Коэффициенты BNn, DN2 и ENn, а также Fn раз­личны для каждого л-го уравнения и изменяются от одного времен­ного шага к другому вместе с изменением М, так что параметры Е, DA, Q, L и W, а также граничные условия могут изменяться произвольным образом.

Осесимметричный перенос характеризуется математическими моделями, которые представлены особым видом уравнения (7.12) с В=2пг, так что нет необходимости рассматривать указанный случай специально.

Двумерный конвективно-диффузионный перенос. Наиболее из­вестными методами численного решения на ЭВМ задач двумерно­го конвективно-диффузионного переноса, описываемого дифферен­циальным уравнением вида

(DtJL)-Vl±„~noJL+ic-w (7.13).

Dxi \ dxi f dxi dt

При /=1, 2, соответствующих направлениям координат х, у, явля­ются методы характеристик, случайного блуждания (Монте-Кар­ло) и конечных элементов.

В методе характеристик временные изменения концентрации dc/dt в уравнении (7.13) делятся на три части, соответствующие проявлению конвективного переноса (dc/dt) и дисперсии (dc/dt) 2, обменным процессам и источника-стока (dc/dt)3 и имеющие вид.

(dc/dt), = - (vjn0) (дс/дХі), (7.14)

(dc/dt)2 = (І/я,,) (д/дхй (Адс/дХі), (7.14а)

(dc/dt)з = (Х/л0) с — w/n0. (7. Не­

Соответственной декомпозиции подчиняются, разумеется, и гра­ничные условия.

Решение уравнения (7.14) для каждого пространственного узла k, I согласно временной дискретизации исходит из представления

(dc! dt), = (c<+f<-cltl)iU,

Где с*кі установлено из решения на предыдущем интервале вре­мени.

Для определения величины cffi* служит способ блуждаю­щей точки. В этом способе маркируются точки поля потока, кото­рые блуждают как центры тяжести определенного количества ве­щества со скоростью Ui—v/n0=vx/n0-\- Vy/n0. Концентрация ct+ft получается при этом как сумма вещества, поступающего в блок k, /, отнесенная к объему воды в блоке.

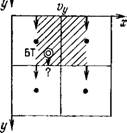
Основная задача метода случайных блужданий состоит в том, чтобы возможно точнее и с наименьшими затратами установить местоположение каждой блуждающей точки ко времени t-\-At. Для этого необходимо знать непрерывное распределение компо­нентов скоростей vx=vx(x, у) и Vy — Vy(x, у). Они определяются через производные от напора, распределение которого получается. аналитическими или численными решениями соответствующей гео­фильтрационной задачи. На рис. 26 представлены три способа численного определения скоростей фильтрации путем билинейной интерполяции.

Ух

DII> сж>

Рис. 26. Схема билинейной интерполяции пространственно-дискретизированных компонентов скорости фильтрации vx и vy для случаев их задания на границах элемента (а), в узле элемента (б), а также на границах и в узле элемента (в). 1 — узловые точки; 2 — блуждающая точка; 3 — область блуждания 128

Местоположение блуждающей точки ко времени t-j-At устанав­ливается по местоположению во времени t из выражений

Хр*'К К' УІ)+< Іх'+Л(< у?*')+<+Л( УІ) +

+ у'+л*)]\ (7.15)

УІ) Уг+Л{)К УІ) +

+ /vt+at(xt+atf yt+at^f {7ЛЪа)

Где координаты и у*+л* в правых частях уравнений уста­навливаются итеративно. Обычным является отказ от итераций, и тогда в правой части задаются х(+Лі — х(т и у*+йі При этом шаг по времени должен ограничиваться таким образом, чтобы препятствовать продвижению блуждающей точки в преде­лах каждого временного шага на расстояние, превышающее раз­мер пространственного шага сетки, т. е. должно соблюдаться усло­вие

.. , а&х,, . аДу

М <:----------- , <----------- У--- .

(Уд/Ло)тах (fy/«o)max

В то же время приведенный в работе [61] тест показал, что путь должен быть больше, чем расстояние между стартовыми точ­ками блужданий, чтобы уменьшить осцилляцию результатов. При распределений четырех блуждающих точек в квадратном блоке рекомендуется а=0,75, а при девяти точках а=0,5.

В точках Источников непрерывно стартуют нбвые блуждающие точки, а в точках стоков они погашаются. В некоторых случаях может оказаться необходимым в определенные периоды времени реализовать новые распределения стартов.

Уравнения (7.15, а) решаются на основе конечно-разностной аппроксимации. При доминировании конвективного переноса над дисперсивным используется явная расчетная схема [у—0 в урав­нении (7.1)]. Однако в случае, когда явная схема в соответствии с критерием

2 Dx, 2D

{lxy ' (ду)>

Требует слишком маленького значения шага At, в виде исключе­ния может быть эффективным использование неявной схемы, на­пример, с у=0,5.

Уравнение (7.14,6) также решается по явной схеме, хотя хо­рошие результаты может дать и применение квазинеявной схемы при 7=0,5. Ограничения временного шага для этого решения опре­деляются условием, что изменение количества вещества в блоке за

Алгоритм метода характеристик не требует для моделирования миграции решения системы уравнений. Достоинство этого алго­ритма — быстрота. Недостатком его являются большие затраты времени на размещение вычислительной программы в ЭВМ.

Примеры вычислительных программ по методу характеристик приведены в работе [61], где для решения фильтрационной зада­чи использована конечно-разностная аппроксимация с неявной схе­мой переменных направлений. Приведенным в работе [61] реше­нием тестовой задачи показано, что лучшие результаты дают де­вять стартовых точек блуждания в каждом квадратном элементе. Достоинство этой программы проявляется в контрольном состав­лении баланса вещества на каждом интервале времени. Последо­вательное усовершенствование декомпозиции (комбинированное рассмотрение Эйлера—Лагранжа) описано в работе [70].

Метод случайных блужданий (Монте-Карло) также базирует­ся на декомпозиции миграционной модели на три части. Конвек­тивный перенос, как и в методе характеристик, моделируется по способу блуждающей точки. Определяемые таким путем положе­ния блуждающих точек рассматриваются в статистическом смысле как ожидаемые величины. В методе случайных блужданий детер­министические рассуждения метода характеристик для процессов переноса преображаются в стохастические.

Описываемое с помощью уравнения (7.14,6) влияние процес­сов обмена и превращений, а также источников-стоков должно учитываться путем корректирования в каждой точке блужданий представительного количества вещества га, которое на каждом временном шаге для точки с номером k в простейшей форме будет:

Где AV— объем элемента, в котором находится k-я блуждающая точка во времени kr — общее число блуждающих точек, на­

Ходящихся ко времени в этом элементе.

С точки зрения проведения вычислений метод случайных блуж­даний точек по сравнению с методом характеристик имеет следу­ющие преимущества: выпадает решение уравнения (7.14, а), что при использовании эффективного генератора случайных величин возмещается ускоренным построением программы; пространствен­ная сетка необходима только для решения фильтрационной задачи и подлежит поэтому лишь небольшой реконструкции; распределе­ние концентраций, которое в методе характеристик устанавливает­ся на каждом временном шаге, рассчитывается только по заданию вычислителя, что сокращает расчетное время; это единственный способ, позволяющий простейшим образом учитывать возрастание
.дисперсивности с увеличением пути переноса; метод требует ми­нимальных затрат для моделирования переноса многокомпонент­ных и взаимосвязанных мигрантов; при повторных расчетах оди­наковых примеров отчетливо виден стохастический характер, та« что может быть полезнее, например, решать задачу 10 раз с 200 блуждающими точками, чем один раз с 2000.

К недостаткам метода случайных блужданйй можно отнести необходимость сравнительно большого числа блуждающих точек, гарантирующего достаточно гладкий результат, а также то, что при выборе сравнительно грубой дискретизации внутри обла­сти концентрация может оказаться больше гранйчных зкачений.

Примеры вычислительных программ по методу случайных блужданий приведены в работе [13] с использованием для реше­ния фильтрационной задачи неявной конечно-разностной аппрок­симации на прямоугольной сетке и неявного метода переменных направлений.

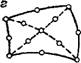
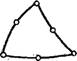
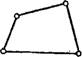
Метод конечных элементов для моделирования миграции почти исключительно использует алгоритм, базирующийся на формули­ровке Галеркина. Хорошо обоснованной, отработанной и опробо­ванной считается программа FBElOW, представленная в работах [50, 51]. Эта программа охватывает одновременно определение поля скоростей и концентраций конечно-элементной аппроксима­цией. Можно выбирать элементы различной формы (рис. 27), од­нако прежде всего оказываются пригодными изопараметрические криволинейные четырехугольные элементы с биквадратным мате­матическим выражением (восьмиточечный элемент, см. рис. 27, г).

В качестве первичных неизвестных вводятся как Я, с, так и естественные переменные Я, vx, vy, с. При формулировке фильтра­ционной задачи в напорах необходимые в дальнейшем скорости фильтрации получаются из поля напоров путем дифференцирова­ния. Выводимые при этом математические функции Для vx и vy таким образом еще только билинеарные. Поскольку такая форму­лировка не обеспечивает устойчивого состояния для vx и vy, осо­бенно при возможности значительных различий скоростей от эле­мента к элементу, то рекомендуется формулировка, включающая в первичные переменные скорости vx и vy. В четырехугольном эле­менте определяются дискретные величины Я, Vx, Vy, с в угловых точках и значения vx, vy, с в точках середины сторон. Такая ап-

Рис. 27. Схемы изопараметрических конечных элементов плоского потока.

■Элементы: а — треугольный с линейными соотношениями; б — четырехугольный с билнней - .ными соотношениями; в — треугольный с квадратичными соотношениями; г — четырех­угольный с биквадратными соотношениями

Проксимация гарантирует для (компонентов скорости третий поря­док [51].

Для временной аппроксимации в программе FEELOW возмо­жен выбор неявной схемы (у— 1) или схемы Кранка—Николсона (у=0,5) с порядком аппроксимации At или At2.

Так как при у— 1 вводится численная дисперсия с погрешно­стью AD = Atv2/2n0 [см. уравнение (7.5)], это соответственно ли­митирует величину At. Поэтому в области времени, в которой не вводятся скачкообразные изменения на границах, используется не­стабильная, но более точная схема Кранка—Николсона, причем для стабилизации рекомендуется предварительно задавать внут­ренние граничные условия второго рода для конструкции [51].

После пространственной и временной дискретизации составля­ется система уравнений

[Л] [X(t + M)} = [B] {X(t)) + {F(t)\

С субвектором Xi — Xi(Hi, Vx, i, Vy, i, Сі) в точке і, [ ] и { } — символы матрицы и вектора. Эта система несимметрична и реша­ется посредством так называемого фронтального и профильного алгоритма [50]. Величины, входящие в матричные и векторные элементы А, В и F, принимаются в FEELOW поэлементно постоян­ными. Вычисление двойных интегралов проводится посредством ЗХЗ-квадратной схемы Гаусса. Программа записана применитель­но к машине БЭСМ-6.

Посредством программы FEELOW решался пример для харак­терной области береговой фильтрации к водозабору (рис. 28) при дискретизации поля с 96 четырехугольными элементами, 347 узло­выми точками и общим числом 1168 неизвестных #,, vxj, vy, i и ct.