Моделирование миграции подземных вод

Опыты в сосудах-реакторах

С помощью опытов в сосудах-реакторах используются процессы накопления и превращения мигрантов на пробах породы как эле­ментах подземной многофазовой системы. Процессы переноса при этом не принимаются во внимание. В экспериментах исследуются пробы пород с нарушенной и ненарушенной структурой, ненасы­щенные, насыщенные или пересыщенные водой.

Для миграционной модели в данных условиях получается как бы один узловой элемент, включающий элементы накопления и реакции превращения. Математическая модель миграции вещества в сосуде-реакторе описывается уравнением

R + ARn~=dSldt, (8.1)

Где Я —суммарная скорость реакции (превращения вещества) в сосуде-реакторе; Д/?п — скорость внешней подачи вещества в со­суд-реактор; S —количество вещества, накопленного в сосуде-ре­акторе;

После ввода конкретных моделей накопления и реакции полу­ченное обычное дифференциальное уравнение решается аналити­чески или численно. Для наглядности изображения типичных проб - лем и особенностей их решения рассмотрим некоторые варианты таких опытов.

Вариант 1. При пренебрежимо малой скорости превраще­ния Вещества и AR„, не зависящей от S, из уравнения (8.1) получим:

Si+i - St = J ДRndt = с0 bvf - ct Д©0/,

Где Si и с{ — соответственно накопившееся количество вещества и его концентрация в сосуде-реакторе в подвижной жидкой фазе на момент времени і; ДУ;° и AV0i—объемы флюида, добавленного в сосуд-реактор и отобранный из него на момент времени і; с0 — концентрация вещества в объеме ДУЛ Этим соотношением можно пользоваться, если U+г—ti~>tR [см. уравнение (5.1)], т. е. если для с в сосуде-реакторе устанавливаются усредненные по объему соотношения.

Для S получим:

S = S0 + SH = cV0 + Мип/рп,

Где V0 — объем подвижной флюидной фазы; ^ == Д1/,° — — ДІ/oj; N — удельная объемная емкость накапливающегося ве­щества; тп — масса пробы породы в сосуде-реакторе; рп — плот­ность породы с неподвижной частью флюида. При известных на­чальных значениях S] и V0l величина SH определяется кумуля­тивно по графически заданной характеристике накопления Л/г = —f(Ci) и соответствующей математической модели [например, по> уравнениям (5.3) — (5.5)]. Если начальные значения S, и V0l a priori неизвестны, то выражение

SH/+ = SBl+clV0rcMV0M+ct°bVl°-clbV0l (8.2)

После введения смыслового члена для N [например, соответствую­щего уравнениям (5.3) — (5.5)] составляет систему уравнений, из которой определяются неизвестные параметры и начальные зна­чения выбранного уравнения Процесса накопления. Целесообразно' составить программу для расчета такого процесса на ЭВМ. Одно­временно из заданных моделей выбирают модель процесса накоп­ления, которая наилучшим образом приспосабливается к опытным данным.

Вариант 2. Если не происходит привноса вещества в сосуд- реактор или отбора из него (Д/?п=0), то7, например, при выборе - изотермы Генри (5.3) как модели накопления вещества и г0~КоС2,. Гн=КнС2 [см. уравнение (2.12)] в качестве модели превращения; вещества в подвижной и неподвижной фазах Иолучим

(V0 + KdmJPtt) dcjdt - —(K0V0 + К«ти1Рп) с2.

Решение этого уравнения дает

С 1 = c0_1 + at\ с0 = с/=0,

А = (K0V0 + KHmJPa) (V0 + KdmJPa).

144

В большинстве случаев опыты в сосудах-реакторах проводят при ЯфО в насыщенных водой пробах {Уо=пйУ) для того, чтобы раздельно не рассматривать Ко и Кн. Тогда имеют силу соотноше­ния V0+Kdma/pn = V(n0+Kd) и KoVo+Knmnfpn—KV, где V — объ­ем образца породы.

При сложных моделях накопления и реакций окончательные аналитические решения уравнения (8.1), вообще говоря, недости­жимы. В таких случаях уравнение (8.1) решается численно и па­раметры данных моделей определяют посредством идентификации, например, с использованием какой-либо функции качества.

В зависимости от того, движется твердая или жидкая фаза в сосуде-реакторе или нет, различают статические и динамические опыты, хотя движение при этом только ускоряет процессы обмена и, по существу, не изменяет модели лабораторного процесса.

При статических опытах порода и жидкость остаются в тече­ние всего опыта в сосуде-реакторе неподвижными. Процессы рас­пространения внутри сосуда-реактора происходят при статических опытах лишь путем диффузии. Сосуд-реактор при этом рассмат­ривается как представительный элемент VR (см. гл. 5).

Представительное время tR может оказаться довольно большим и требует длительного Опыта. Если считать, что образец породы со­стоит из агрегатов, характеризующихся средним размером d*, то, анализируя диффузионный поток в шарообразном агрегате, можно показать, что представительное время концентрационного выравни­вания вещества в агрегате можно оценить по соотношению

F - v nd*\ ,,_ 1 lr 6

Ч — /.-77-» /. —г:г in—- >

Du 4r.2 п-о

Где п — пористость агрегата; б — относительная разница содержа­ния вещества в агрегате и на его поверхности.

Рассмотрим для примера опыт по установлению количественной модели на­копления в породе фосфора Р043~ в случае увеличивающейся концентрации при условии пренебрежения превращением вещества (R—0). Модель разрабатыва­ется в условиях насыщения водой (Vn= (1—S — S/V и AV'°— ==Vro). Согласно уравнению (1.4) получим

S„m - SH/ + П0 (et - o+i) + (c/> - q) AV0/V

Или Si+i = Si+(Cj°—c<)AVG/V=Si + Am,/V. Измеренные значения сі ft = 1, 2...) и соответствующие значения S и SH приведены в табл. 10. Предварительным опытом было определено п0 = 0,25 hSH] — 1.4- Ю-4 мг Р013- = Р на кубический сантиметр (табл. 10) породы.

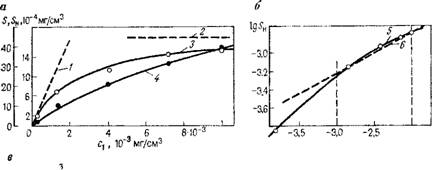
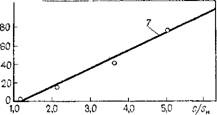
На рис. 34,а представлены графики S=S(c) и S„=S„(c). Если зависимость не прямая, то в качестве модели процесса накопления используются нелинейные уравнения N(c), например изотермы Ленгмюра или Френндлнха (см. рнс. 34,6, в).

Если модель процесса накопления соответствует уравнению (5.5), можно нанести опытные точки в билогарифмических координатах, которые должны рас­положиться на прямой линии, что для замеренных значений в рассматриваемом опыте выполняется для относительно большой области 1 • 10~3<с<1 • Ю-2 мг/см8. Если процесс накопления удовлетворяет модели, описываемой уравнением (5.4), требуется, чтобы на прямой линии соответственно располагались замеренные значения (см. рис. 34). Параметры модели процесса накопления также опре­деляются в этом случае из параметров уравнения прямой.

Динамические опыты в сосудах-реакторах производятся с дви­жущимися жидкостью или образцом. При задании вынужденного движения жидкости ускоряются процессы распространения и пе­ремешивания внутри сосуда-реактора, что сокращает время опыта. На основе временных констант, полученных при опытах в относи­тельно небольших сосудах, можно получить время стабилизации такого процесса в статическом состоянии: tCi= (S/c)R= (0,5VS/c)/ (DM©//)^0,5-20 см3-0,5/(10-6 см2/с-7,37 ем2/2,7 см)^2 сут.

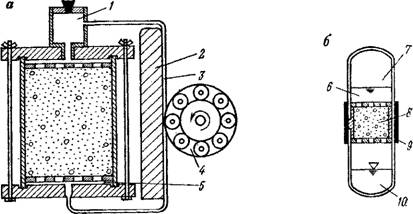
Для проведения такого рода опытов циркуляционное движение жидкости можно создать, например, с помощью перистальтическо­го насоса (рис. 35,а). С учетом превращения вещества (##0), добавленный объем (в рукаве отвода, распределяющем простран-

Ft)

Рис. 35. Динамические опыты в замкнутых сосудах-реакторах с принудитель­ным перемещением жидкой фазы.

А — циркуляция подвижной фазы с помощью перистальтического иасоса, б и в — промывка пробы породы в медленно вращающейся мешалке, 1 — мерник для загрузки вещества и удаления воздуха; 2 —- проба породы; 3 — трубка обратной подачи; 4 — вращающийся кор­пус со свободно вращающимися валиками; 5 — распределяющие полости; 6 — затопляемое пространство; 7 — воздух; 8 — проба породы; 9 —резиновая манжета; 10 — жидкая фаза; 11 — ротационная мешалка

Стве) должен быть относительно мал в сравнении с rioV, чтобы не учитывать его специально в модели реакции и накопления. В про­тивном случае поправки в этих моделях, учитывающие такие час­ти устройства, как рукава отвода, распределяющие пространства и накопительные сосуды, нужно оценивать по данным предвари­тельных опытов.

Если жидкая фаза многократно пропущена через образец, то состояние равновесия обычно достигается через несколько часов (до нескольких дней). Скорость потока не должна существенно превышать коэффициента фильтрации образца. Другие циркуля­ционные экспериментальные устройства и сосуды-реакторы для определения значений Ка описаны в работе [63].

В устройствах, рассмотренных в работе [60], движение жидко­сти происходит под действием силы тяжести в очень медленно вра­щающейся ротационной мешалке (см. рис. 35, б). Здесь необходи­мо быть уверенным, что постоянное смешение опытной жидкости и газа (в основном воздуха) в обоих пространствах внутри сосуда не влияет на исследуемый процесс. Скорость циркуляции должна быть выбрана так, чтобы за один оборот перетекала почти поло­вина жидкости пространства пробы. В наиболее характерном ва­рианте опыта в сосудах-реакторах перемешиваются порода и жид­кость обычно так, как это показано на рис. 35, в. Проба измельчен­ной породы свободно помещается в опытную трубку (сосуд-реак­тор) и падает при каждом перевороте жидкости в сосуде (обычно с частотой 10—20 переворотов в минуту). Эти лабораторные тесты очень просты и технически наименее трудоемки.

Существенным недостатком опытов в сосудах-реакторах являет­ся то, что в них практически не достигается состояние стабильного равновесия, поскольку возможности поглощения постоянно изме­няются, обычно увеличиваясь в связи с ростом удельной поверх­ности и образованием новых нарушенных поверхностей [60]. По­этому опыты в сосудах-реакторах имеют ограниченную область применения, и их достоверность должна в каждом случае обосно­вываться.