Моделирование миграции подземных вод
Опыты в фильтрующих образцах
Фильтрующие образцы (нарушенного и ненарушенного строения) имеют сравнительно небольшие размеры (обычно 10—20 см). На таких образцах целесообразно определять параметры обменных лроцессов между твердой и жидкой фазами, с учетом физико-химических превращений в жидкой фазе, а также происходящих в связи с этим изменений проницаемости пород.
Методика интерпретации фильтрационных опытов разобрана ниже. На примерах этих — наиболее простых — опытов рассмотрены различные методические предложения, которые могут использоваться для интерпретации полевых опытно-миграционных работ. Эти опыты рекомендуется проводить при ненарушенном строении образцов с раствором, возможно близким к тому, который предполагается в натурных условиях.
Для получения более ясной схемы проведения опыта породу в колонне сначала насыщают раствором с постоянной исходной концентрацией трассера с0 и выстаивают до наступления равновесия. В начальный момент проведения опыта во входном сечении колонны с постоянной скоростью подается трассерный раствор с концентрацией с0, которая может меняться во времени. Обычно такие опыты проводятся при постоянной входной концентрации трассера; для экономии трассера и более рельефного проявления процессов дисперсии проводятся также опыты с трассерным «пакетом», когда трассер с концентрацией с0 подается с момента t=0 до момента to, после чего подается исходный раствор (с концентрацией с0). В процессе опыта прохождение трассера фиксируется в выходном сечении (выходная кривая), а иногда также путем отбора проб или по датчикам в промежуточных сечениях. 148
В связи с небольшими размерами образца считается, что для иего характерна схема гомогенной среды. Дифференциальное уравнение переноса для такой схемы с учетом обменных процессов имеет вид
Дс. dN. дс д2с
И--------------- 4-і;------ = О гг— ,
0 dt dt ^ дх
Оно должно решаться совместно с уравнением кинетики обмена. Если можно пренебречь кинетикой обмена, считая сорбционные процессы равновесными, то это уравнение принимает вид
TOC \o "1-3" \h \z дс. дс —, дч, ,, /о
П —- + © — = 0 —; n=n9 = n0 + Kd. (8.3)
Dt dx дх2
Для такой модели переноса на входной границе колонны (образца) должно задаваться граничное условие vc°=[vc— D (dc/dx)]0,t, а на выходной границе — условие dc/dx=0, однако для чисел Пекле Pe=u//Z?>20-f-30 это условие на входной границе можно заменить более простым с=с°, а выходную границу относить в бесконечность [56].
Нейтральный трассер. В случае использования нейтрального трассера в уравнении (8.3) «=«0, и искомыми параметрами являются величины По и D.
Прежде всего рассмотрим опыт с постоянной подачей трассера, когда опытные данные обрабатываются на основе решения фундаментальной линейной задачи микродисперсии при фильтрации в колонне длиной I, первоначально заполненной раствором с концентрацией с0, при подаче в нее с момента £=0 раствора с концентрацией с0.
Для обработки опытных данных удобно использовать предложенную Д. Роузом и Д. Пассиоурой [74] аппроксимацию аналитического решения (6.18) в виде
С = 0,5erfcЛ; , (8.4)
Vt 4 А
|
Где величины А и В зависят от числа (параметра) Ре (табл. И). Таблица 11 Зависимость величин А и В от параметра Ре
|
При расчетах опытных параметров в соответствии с выражением (8.4) по данным выходной кривой строится график зависимости величины |=inferf (1—2с) от lg/, уклон которого |'= = A|/Algtf численно равен величине 2,3 А. По этой величине с помощью данных, представленных в табл. 11, находится значение параметра Ре, причем для удобства интерполяции лучше по табл. 11 находить значения Ж и по ним считать Ре=(2А/А)2. По этому значению параметра Ре определяется значение D=t)l/Pe. Затем по любой паре значений \gt, снятой с прямой, получается величина активной пористости из выражения
6 vt А
Или
Vt ( Аг + 0,25В \
«.- — ex р( ^ ).
Для обработки такого опыта эффективно использование интегральных преобразований концентраций по Лапласу—Карсону,. изменение которых описывается уравнением (6.17), в котором параметр а находится из выражения
A2D-\~av = n0p. (8.5)
При таких расчетах прежде всего определяются значения интегральных изображений относительных концентраций С при различных р (см. прил. 2). После этого для каждого значения р находится параметр а:
/ С I 6 с к '
Если имеются данные замеров на разных расстояниях х от входного сечения, то при каждом р строится график в координатах —lgC и х, на котором опытные точки должны лечь на прямую линию, проходящую через начало координат, что является диагностическим признаком применимости решения (6.17).
Получив значения а(р), следует нанести их на график, построенный в координатах а и р/а, где согласно уравнению (8.5) опытные точки должны лечь на. прямую линию, отсекающую на осях отрезки a0~—v/D и (p/a)o=v/ti0, по которым находятся значения параметров.
Для удобства интерпретации опытных данных целесообразно подобрать параметры опыта так, чтобы иметь возможность описать выходную кривую зависимости относительной концентрации трассера с(0 уравнением (6.20):
?=0,5ErfcE=0,5(l-e, U); ї-і^-Л^,. (8.7)
Как показывает теоретический анализ [29], для применения этого уравнения требуется ограничить длину образца I и расчетное время опыта t неравенствами
T>[2і/----------- ЛЗІ, (8>8)
Vbn [ V bD+bn I V
Тде 6n и 6d — допустимые погрешности определения параметров по и D. Обработку выходной кривой по уравнению (8.7) целесообразно проводить следующим образом: по выходным данным при известном значении с находится аргумент § из уравнения erf g= 1—■ 25 (учитывая, ЧТО функция erf является нечетной, Т. е. erf (-—ig) ===== =—erf I), после чего строится график зависимости от t, который, как это следует из выражения (8.7) для I, должен быть прямолинейным и описывается уравнением
* уТ = 0,5 (8.9)
По точке tQ на пересечении этой прямой с осью і находим активную пористость из соотношения
= (8.9а)
Затем по любой точке (с координатами и і) на построенной прямой линии определяется коэффициент микродисперсии:
Достоинством такого способа обработки является возможность диагностической проверки используемой расчетной зависимости по тому, насколько хорошо опытные точки графика зависимости l~]/t от t ложатся на прямую линию.
Если при проведении опыта имеются замеры значений в промежуточных точках опытной колонны на расстояниях х от входного сечения, то для более полного обобщения («свертывания») информации целесообразно провести комбинированное прослеживание, представив выражение (8.9) при 1-х в виде
Х ' г D \ щ х}
При этом все опытные данные наносят на график, построенный в координатах z=%]/t/x и x—t/x. На таком графике все опытные точки должны лечь на одну прямую, что является очень сильным диагностическим признаком правильности исходной математической модели. Если это условие выполняется, то по точкам г0 и то, которые образуются при пересечении прямой, проведенной по опытным точкам с осями z и т, получим значения параметров
K0 = vx0 и D — . 0 0 4*0»
Как заметил Л. Лукнер [65], в этом случае можно воспользоваться аппроксимационным выражением (8.7) при
\ — 0,5 У^у In. (8.10)
Для обработки данных комбинированного прослеживания (при отборе проб в нескольких сечениях) согласно уравнению (8.10) опытные данные наносятся на график, построенный в координатах 1/Удс и lg(x/t). На этом графике опытные точки должны ложиться на одну прямую линию, причем по точке (x/t)о пересечения логарифмической прямой и оси x/t и по наклону 0=А (І/У*)/Alg (.*:/£) определяются значения параметров
И D =
С*/Оо
При малом числе опытных точек, когда диагностический анализ становится нереальным, параметры л0 и D определяются по двум элементам выходной кривой: времени to прохождения фронта индикатора, фиксируемого при с=0,5, и наклону ct выходной кривой к оси t в точке t=t0(ct~dc/dt при t=t0). При этом величина п0 определяется по уравнению (8.9, а) а параметр дисперсии — по формуле
4 *Vo8
Рассмотрим особенности обработки опыта с запуском трассерного «пакета». Для условий такого опыта зависимости, описывающие распределение концентрации раствора, могут быть получены по принципу суперпозиции, как для ступенчатого закона изменения граничной функции, когда в начальном сечении задается условие с= 1 при O^t^t0 и с=0 при t>to. Например, принимая за основу упрощенное выражение (8.7), получим уравнение для выходной кривой при подаче трассерного пакета:
С = erfcг — erfcS0, % = S0 — (8.11)
0 2 У n0Dt 0 2 У n0D (t — <o) v '
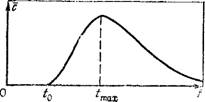
Выходной график, описываемый этим уравнением, представлен на рис. 36. Анализ показывает [37], что время /тах продвижения пика концентрации практически соответствует бремени движения середины трассерного пакета, откуда следует простая формула для определения пористости:
N0 = v(tmax-0,5t»)!L (8.12)
Обработку такого опыта удобно проводить, используя решение задачи в интегральных преобразованиях по Лапласу—Карсону, которая в этом случае имеет тот же вид, что и при постоянном запуске трассера. Рекомендации по расчетам изображений для формы графика c(t), характерной для запуска трассерного пакета, приведены в прил. 1.
Сорбируемый трассер. Способы обработки опытов с сорбируемым трассером существенно различаются в зависимости от типа изотермы и проявлений кинетики сорбции. Если при линейной изотерме вида (3.2) можно пренебречь кинетикой сорбции, Л/. л
Тп пгтяютгя в липр ичппжрншр рис• 36■ Формы выходной кривои,
То остаются в силе изложенные получеНной по результатам запуска выше расчетные зависимости для трассерного пакета нейтрального трассера, в которых вместо активной пористости
П0 вводится эффективная пористость (емкость) пэ, выражаемая согласно уравнению (5.1а). При этом для определения активной пористости и коэффициента дисперсии используются данные о прохождении несорбируемого трассера.
При наличии замеров в различных сечениях колонны лучшее обобщение этих данных (комбинированное прослеживание) достигается, если из (8.4) величину пэ выразить формулой
В ходе расчетов по формуле (8.13) значения А определяются при среднем D из полученных расчетами по разным сечениям. Если при этом оказывается, что значения пэ имеют выраженную тенденцию к изменчивости, то для достижения наилучшей стабильности параметра пэ можно варьировать величиной D.
При линейной изотерме с учетом кинетики сорбции в гомогенной среде процесс описываётся системой дифференциальных уравнений (8.1) и (3.7).
Для обработки опытных данных по фильтрации сорбируемого трассера при линейной 'кинетике сорбции рекомендуется использовать решение задачи переноса в изображениях по Лапласу—Кар - сону в форме 6.17, которое имеет вид (6.18), причем для величины а справедливо соотношение
A2D +m.-v = ппр --------------- ^f - . (8.14)
ЯкР +р
Для расчетов целесообразно преобразовать выражение (8.14) к виду
+ (8.15)
Где
AsD + av — asp
|
|
При расчетах по этим зависимостям необходимо предварительно при различных величинах р установить значения изображений ср относительных концентраций, а также соответствующих значений f^ln-Cp-1. Получив таким образом зависимость а(р), сле
дует при значениях D и п0, определенных по данным миграции не - сорбируемого трассера, установить величины А и нанести опытные - точки на график зависимости А(р). Согласно уравнению (8.15) эта зависимость должна быть прямолинейной, причем по точке А0у, образующейся при пересечении такой прямой с осью А, и по наклону этой прямой получаются сорбционные параметры Э=Л0 и ак=Ар/АА.
При переменной скорости фильтрации или нелинейной изотерме сорбции для обработки опытных данных целесообразно применять конечно-разностные уравнения. Рассмотрим такое решение для конвективно-диффузионной модели переноса, записав уравнение (8.3) в форме
Nc,+vcx=*Dcxx. (8.16)
Существенное значение имеет форма конечно-разностных выражений производных, которые рекомендуется давать по достаточно подробной шеститочечной схеме в виде
Ct в 2дГ 1-1 + 1+1 + ^ 17)
Ах \ Axi+1 Axt. t }
Где Aic,--i=aA*i_i/2A*; Act~c'—c°; Axi+i — xi+l/2Ax; Ах—0,5(A*/-i-h + Д*ж);с=0,5(с'+с°).
При малой значимости дисперсионного члена Dcxx можно вести расчеты отдельно в интервале сечений і—1, і и і, г'4-1, считая ct и сх по четырехточечной схеме, т. е. в интервале сечений і—1, і
С = 4 ~~Сы с = +
* 1 2At '
А в интервале сечений г", t'-f-l
С.+1 — а Асі + Дсг+1
Ах-М 2А t
Обработку опытных данных по конечно-разностным уравнениям для определения эффективной пористости (емкости) пэ целесообразно проводить в тех случаях, когда параметр дисперсии D можно считать известным из расчетов по нейтральному трассеру. Тогда
N = na=*-}-(Dcxx — vcx). (8.20)
Кроме того, для приближенных оценок при постоянном значении v можно совместно определять величины п и D. Для этого исходное уравнение (8.16) делится на величину vcx и приводится к виду
N? i (с) + 1 — О'Ъ (с), <Р, (с) = cti(vcx), ср2 (г) = cj(vcx). (8.21)
Для обработки опытных данный по уравнению (8.21) рассчитывают на различные периоды времени значения фі и <р2 и строят график зависимости между ними, на котором, согласно выражению (6.19), опытные точки должны лечь на прямую линию. На осях Зта линия отсекает величины <рі° и 'ф2°, по которым получают значения расчетных параметров:
D — 1/<?2° и Л = — 1/<р,°.
Использование конечно-разностных уравнений правомерно в условиях, когда производные по расстоянию не слишком сильно изменяются в пределах расчетного интервала времени At, а производные по времени — в расчетных сечениях. Количественное обоснование возможностей применения этих уравнений целесообразно приводить на тестовых примерах, имеющих более точное решение.
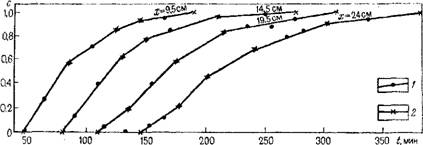
Пример обработки лабораторного опыта по фильтрации сорбируемого мигранта в образце. Опыт проводился с образцом среднезерннстого песка, загруженным в трубку диаметром 5 см и длиной 24 см, в которой на расстояниях 4,5; 9,5; 14,5 и 19,5 см от входного сечения сделаны слнвные отверстия для отбора проб. Образец предварительно насыщен дистиллированной водой, после чего во входном сечении задана непрерывная подача раствора СаС12 (0,005 н.) с сорбируемым трассером 45Са. Графики изменения относительных концентраций раствора в различных сечениях представлены на рис. 37.
Расчеты ведутся в интегральных изображениях, значення которых рассчитываются по формуле (П.1) прил. 2. Аппроксимация опытных точек ломаными линиями, использованная для таких расчетов, показана на рис. 37, причем во всех случаях аппроксимирующая линия состояла из четырех отрезков (п.—4). Исходя из приведенных в прил. 2 рекомендаций, выбирались значения tp в пределах от 30 до 60 сут, причем расчеты по формулам (П.1) н (П.2) дали практически совпадающие результаты.
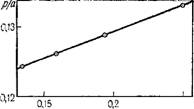
Эти данные наносились на полулогарифмический график зависимости С от х, где при различных р по Опытным точкам проводились прямые линии, по уклону которых находились значения а согласно формуле (8.6). После этого строился график в координатах а—р/а (рис. 38), на котором проводилась прямая линия, имеющая координаты а0=—1,45 и (р/а)о=0,113. При скорости фильтрации о = 0,335 см/мин получается £>==0,335/1,45=0,23 см'/мин и пэ — = 0,335/0,113=3. Отметим, что в таком расчете проявляется высокая чувствительность определения величины D по отношению к рассчитываемым значениям
|
Рис. 37. Графики изменения относительной концентрации мигранта 45Са прн опытах в фильтрующем образце в сечениях 9,5; 14,5; 19,5 и 24 см [66]. 1 — опытные точки; 2 — точки излома аппроксимирующего графика |
|
0,25а Рис. 38. График для обработки опытных данных, приведенных на рис. 37, в изображениях по Лапласу—Кар - сону |
А, требующая проведения прямой в координатах а — pja по уравнению регрессии с определением входных данных с высокой точностью. Для этого же опыта обработкой данных по С1~ получено значение D— = 0,24 см2/мин [66].
|
Следовательно, для такой обработки основными являются ограничения по длине колонны (расстояние от входного сечения до расчетного), а расчетное время может приниматься без ограничений. Для иллюстрации такого расчета приведем два примера при х=24 см. Прн /=165 мин и с=0,126 получаем mterf 1=1—2с=0,748 и по таблице функции; erf, находим 1 = 0,81. Затем рассчитываем с = IVTjl = 0,43 мин°^-см"і т=/// = 6,88 мин-см. При <=268 мин и с=0,798 получаем mferf 1=1— 2с= = —0,404 и по таблице функции erf находим 1=—0,583. Затем рассчитываем; = $ уТ//= —0,4и T=t/l= 11,17 мин-см-1. Полученные таким образом расчетные точки нанесены на график в координатах s, т (рис. 39). Как видно, все опытные точки на таком графике подчиняются практически единой зависимости, удовлетворительно аппроксимирующейся прямой линией, которая дает значения т<>=9 мин-см-1 и g0= 1,77 мин °-5-см-1.. По этим значениям, согласно уравнениям (8.9а) и (8.96), получают значения параметров пэ = 0,335-9 =3,02 и £>=3,02/(4-17,72) = 0,24 см^/мин. Значение D совпало с полученным по данным переноса нейтрального трассера, а пэ — со значением, определенным с помощью приведенного выше расчета в изображениях. Заметим, что при тщательной диагностике данных по графику на рис. 39і можно видеть некоторую тенденцию к криволинейности такого графика'. что,, возможно, объясняется влиянием нелинейности изотермы сорбциш |
Приведем также результаты обработки этих опытных данных по уравнению (8.7). Для проверки применимости этого уравнения используем неравенства (8.8), принимая допустимые погрешности 8п=0,05 и бв=0Д при £>=0,24 см2/мин, г>=* = 0,335 см/мин и я=йэ=3:
Расчеты величины пэ по уравнению (8.13) при значении D = 0,24 см2/мии,. полученном по даииым опытов с нейтральным трассером С1-, дали довольно стабильные значення л3=2,85—3,25, причем нескольк<э меньшие значения получаются при значениях 5=0,4—0,6; среднее значение пэ = 3 соответствует установленным выше другими способами.
Приведем результаты расчетов по конечно-разностному уравнению (8.17) для сечений лгг_,= 14,5 см; дгі = 19,5 см; Жг+і = 24 см в интервале времени 135— 160 мин. По графику, приведенному на рис. 37, найдем значения относительных концентраций в расчетных сечениях: с°/_1=0,68; cj° = 0,19;c0i+1 = 0,01; с'і. і = = 0,81; Ci'==0,45;^+1 = o, l, откуда с,_1 = 0,74; с£=0,32; ё, + 1 = 0,055. При Ддгг_! = 5 см; ДлГг+і = 4,5 см и Дж = 4,75 см имеем Лжг_і = 5: 9,5 = 0,53 и AJcf+1 = 4: 9,5=0,47. При Ас1-1 = 0,81— 0,68=0,13; Лсг=0,45—0,19=0,26; ДСг+і = 0,09 по выражению (8.17) получим значение временной производной относительной концентрации трассера:
0,53-0,13 + 0,47-0,09 + 0,26 _ <Л
С( =-------------------- т.... ' „" ——-------------- = 7,4- 0-з мин-'.
' 2-25
По выражениям (8.18) и (8.19) рассчитываются пространственные производные при средних (по интервалу времени) значениях относительных концентраций: Сг_і = 0,74; ё, = 0,32; с1 + , = 0,055:
|
|
Принимая определенную ранее по нейтральному трассеру величину коэффициента дисперсии D = 0,24 см2/мин, при v = 0,335 см/мин найдем согласно выражению (8.20) величину эффективной пористости:
Пэ = 1А. (0,24-8,7-Ю-з + 0,335.7,21 • 10-2) = 3j56. 7,4-10'3
Определенные таким путем значения пэ для других интервалов в пространстве и во времени приведены в табл. 12; расчеты в интервале 14,5—19,5 см даны без учета влияния дисперсии, т. е. при £>=0.
Значения Пэ подчиняются некоторой незакономерной изменчивости, но хорошо согласовываются со значениями, полученными расчетами по аналитическим решениям.