Моделирование миграции подземных вод
Опытно-миграционные наблюдения за температурой в прибрежном потоке
Интерпретация ОМН, чаще всего осуществляемая численными методами с использованием ЭВМ, направлена главным образом на оценку обменных процессов (см., например, [14]). Вместе с тем в некоторых специфических условиях при сравнительно несложных формах переноса для интерпретации ОМН можно использовать аналитические решения.
Примером таких условий является рассматриваемый ниже случай формирования теплового поля в прибрежной зоне при действии берегового водозабора, где возникают гармонические сезонные изменения температуры. Анализируя такой тепловой поток, можно получить параметры теплопереноса, которые в дальнейшем - могут использоваться для прогнозирования сезонных изменений температуры.
Для такого прогнозирования используется решение задачи теплопереноса в одномерном фильтрационном потоке (в направлении х) с учетом трех форм дисперсии тепла: кондуктивной, гетерогенно-блоковой (теплообмен между проницаемыми каналами и слабопроницаемыми блоками по схеме сосредоточенной емкости) и пластовой (теплообмен в кровлю и подошву пласта по схеме неограниченной емкости). В таком потоке распределение температур в проницаемых каналах 0 и в слабопроницаемых блоках 0* описывается системой дифференциальных уравнений:
TOC \o "1-3" \h \z <30 , . ч <?0* , <30 -,^20. 21' л, .п оч
Спх—- + Сп(1 - У.) _ + = X — 4-------------- б 9.8)
Dt dt dx dx2 m
J®L = a*(b— 0*), (9.9)
Dt
'•'-fl •
OZ \z=±0,bm
Причем температура 0х в кровле и подошве пласта описывается одномерным (в вертикальном направлении) дифференциальным уравнением теплопроводности
, d0' ^ <320
С"-вГ=1!Г>> (9Л0)
Где сп и 1 — соответственно коэффициенты Объемной теплоемкости и теплопроводности пласта; х —удельное содержание проницаемых каналов; а* — коэффициент блокового теплообмена; с — коэффициент объемной теплоемкости воды; т — мощность пласта; v — скорость фильтрации при удельном расходе потока q = vm; А/ и Сп —соответственно коэффициенты теплопроводности и объемной теплоемкости в кровле и подошве пласта.
Поток принимается полуограниченным по длине с периодическим граничным условием
В (0, t) = 6° sin —
To
И произвольным начальным условием.
Решение этой задачи будем искать, задавая 0 в виде
Б==бое-а*8Іпср> 9=s*±_pXt (9.11)
To
Где аир — параметры, определяемые из дифференциального уравнения.
Подставляя выражения для всех членов в дифференциальное уравнение (9.8) и приравнивая коэффициенты при sin<p и eos<p, получим уравнения, связывающие параметры решения аире параметрами процесса:
2 щ 1-х 2\'а'
1------- ГТ^Г" сп-<и*> = х («*-£>)------------ —(9.12Л)
Го 1 + I3 т
2л I 1 — х \ 2Х V
$cv = 2сфХ —------ . (9.12 6}
'о \ 1 +12 / т
|
(9.13) |
Для подбора величин аир при решении прямой задачи можно, выразив р из уравнения (9.126)
2 я / 1 - * \
_ —(*+-+ '
2а а + и
Где
X с 2 А/а'
Сп сп cntn
Подставить затем это выражение в уравнение (9.12а), причем в первом приближении величину р можно рассчитать, принимая а = 0.
Частным случаем этого решения является решение аналогичной задачи для гомогенной среды без учета теплоотдачи в кровле и подошве пласта [23].
Предельное влияние нестационарности, обусловливаемой периодическим изменением температуры на границе потока, оценивается расстоянием хпр, которое получается из уравнения (9.11),. если при х~хпр положить в нем амплитуду изменений температуры равной порогу чувствительности измерений температуры 0пр~ Тогда, принимая 0°=1О° и 0=0,1°, получим
2,3 , ео 4,6 = — lg— = — • а 0пр а
Если пренебречь влиянием продольной теплопередачи и внутри - блоковым теплообменом, то а=б/« и
__ 4,6ц ____ 2,3ис„т / a't«
~*пр~~ є V V я
Где а'—к'/Сп—коэффициент температуропроводности пород в кровле и подошве пласта; q— удельный расход потока; Сп=сп/с~~ •относительная теплоемкость этих пород.
В частности, при характерных значениях, теплофизических параметров $/=0,06 м2/сут; сп'=0,5 получим", что хпр численно равно 200^ (где *пр выражается в метрах, a q в квадратных метрах в сутки). Например, для зоны активного водообмена характерны величины ^=0,1—10 м2/сут, поэтому значения х„р получаются обыч - бо сравнительно ^небольшими, чаще всего порядка сотен метров. Следует отметить, что этот вывод справедлив лишь для водоносных пластов относительно небольшой мощности, когда можно пренебречь поперечным переносом в пределах потока.
При решении обратной задачи по данным измерения температуры 9,- в скважинах, располагаемых на расстояниях Хі От границы, для расчетов параметра а целесобразно использовать значение амплитуды колебаний в скважинах А0г - и на границе А0°, соотношение которых согласно уравнению (9.11) дает
Lg * (9.14)
Хі 8 Mt Д6° v 1
Параметр p определяется по сдвигу фаз AU в 1-м пьезометре:
А _ 2к Ati
Xit0
Для диагностики процесса следует строить графики зависимости lg(l/A0/) и М от хі, на которых опытные точки должны ложиться на прямую линию.
После определения аир можно найти величины § и и, используя выражение (9.12а, б),которые решаются относительно искомых величин:
----- - к 4- а («2 — fJ2 2а;,)
|
|
------------------------------ ; (9.15)
■ а (а2 + ра) [І
|
2к to |
|
1+7)2 |
—------------- . (9.15а)
Дальнейшее решение обратной задачи остается неопределенным, поскольку в общем случае на этом этапе требуется определение входящих в эти выражения параметров и, % и а*, для чего необходима дополнительная информация. В частности, если иметь замеры скорости фильтрации v и принять а, сп и с по литератур-
|
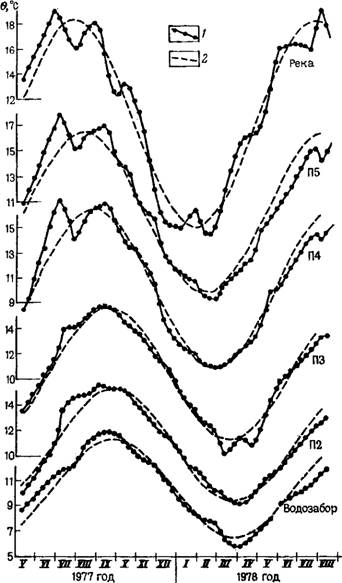
Рис. 43. Графики изменения температурного режима в потоке между рекой н береговым водозабором. 1—2 — наблюденные и аппроксимированные синусоидой температуры соответственно |
Ным данным, то из выражения (9.15), зная u=(c/ca)v, найдем относительное содержание проницаемых каналов
Х = JL [и (р - а) - а (а2 - р2 -2ф)}.
Дополнительные данные режима температуры в кровле и подошве пласта дают возможность независимого. определения величины а', после чего из выражения (9.15а) можно получить значения rj и а*.
Если пренебречь продольной теплопередачей и блоковой гетерогенностью пласта и предположить, что а=0 и 1, то выражения (9.15) и (9.15а) примут более простой вид:
2т. а г
£ — "
<Р-а)«о
Откуда можно найти значения а' и а.
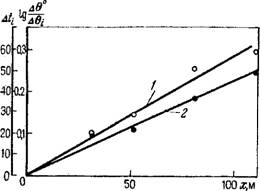
Пример. Рассматривается поток грунтовых вод ме^ду рекой и береговым - водозабором мощностью т=8 м с удельным расходом </=^4,5 м2/сут. Температурный режиі|, замеренный здесь по нескольким наблюдательным скважинам,, показан йа рйс. 43; здесь же приведена аппроксимация натурных тедмограмм синусоидами с их параметрами. По рассчитанным значениям lg(i/A6i) и А^ при различных величинах Хі построены графики, которые приведены на рис. 44. Как видно, опытные данные удовлетворительно ложатсй на прямые линии, расчет по которым дает значения a=5,3-10~3 м-1 и Э= 10—2 м-1. Считая среду гомогенной (х=1) н принимая а=0,05 м2/сут, по формулам (9.15) и (9.15аІ находим, что
7—— • 5,3 • 10-з — 0,05 (28 • 10- в + 1) • 10- 2
Є =_ 365_____________________________________________ =0019 сут-*;
10-2-5,3.10-3 ' Сї '
|
Рис. 44. Расчетные графики обработки данных температурного режима. 1 — график Д 2 —, график lg(A8°/Ae) |
|
365 10-2 — 5,3-10-3 |
= 3,7, м/сут.
При скорости фильтрации v = qfm=0,56 м/сут находим эффективную пористость n=o/u=0,15. Величина п получилась здесь довольно малой, что свидетельствует о существенном проявлении гетерогенности пласта. Определяя при таком значении и коэффициент температуропроводности а из выражения (9.15) и принимая сп=сп', получим а=0,6 м2/сут, что значительно выше обычных значений этого параметра.
|
Если пренебречь гетерогенно-блоковым и пластовым обменом тепла и счи- А а Тать, что 8=0 и х— 1, то из уравнения (9.13а) получим -—' = 77-------------------------------------------- ~ — Р2 _ <х2
Четной схеме значение коэффициента температуропроводности получилось чрезвычайно большим, а значение скорости и оказалось значительно меньшим, чем определенное в предыдущем случае. Это свидетельствует о важности учета гетерогенности пласта при анализе теплового режима в подземном потоке. |
|
И |