Моделирование миграции подземных вод

Модель конвективного переноса

Широкую область применения имеет модель конвективного пере­носа, в которой все дисперсионные эффекты считаются пренебре­жимо малыми. Особенности построения расчетных зависимостей при такой модели обусловливаются структурой фильтрационного потока и моделями физико-химических процессов.

Перенос нейтральных мигрантов. Расчеты конвективного пере­носа удобно проводить по линиям тока, описывая скорость распро­странения мигранта по направлению I вдоль линии тока обыкно­венным дифференциальным уравнением

Где t — время; v = v(l)—скорость фильтрации в сечении распро­странения мигранта; п0 — активная пористость.

Это уравнение решается относительно времени t:

(6.2)

Где С — произвольная постоянная. Зная зависимость v(l), можно получить решение в форме t(l) или l(t). Имея в виду, что v = kl, приведем выражение (6.2) к виду, который может использоваться при известных зависимостях / от напора Я:

(6.3)

Рассмотрим некоторые частные примеры решений, получаемые из этих выражений. При этом будем исходить из представления, что поскольку по сравнению с развитием нестационарных фильтра­ционных процессов миграционные процессы развиваются медлен­но, то при расчетах переноса, как правило, можно принимать ре­жим фильтрации стационарным или квазистационарным [38].

При нагнетании мигранта через скважину в одномерный пла­новый фильтрационный поток напор получается сложением тече­ний одномерного потока в направлении оси х с удельным расхо­дом q0 и радиального потока с расходом Q [38]:

(6.4)

Где Н0 — произвольный напор, определяемый выбранной плоско­стью сравнения. Функция тока представляется при этом выраже­нием

= arctg— .

Х

Положение нейтральной линии (ф=0), ограничивающей об­ласть возможного распространения закачиваемого в скважину ми­гранта, описывается уравнением

Где при г/>О перед правой частью равенства ставится знак плюс, а при у<. О — минус.

Для расчета развития процесса во времени определяется ве­личина

/2 = (1±

{ Т ' 2кТ x* + y*J ' V 2кТ

После чего по формуле (6.3) после преобразований находится вы­ражение

Л — , і sin £

6 = х + In

Sin (£ +у)

В котором

• е = arctg — ; 5 = у-^у.

TimQ х Q Q

В частности, при у=0 получается, что Q=x—ln(l+*). Картина распространения закачиваемого мигранта во времени, полученная расчетами по уравнению (6.1), приведена на рис. 17.

Большой интерес для решения ряда практических задач (на­пример, регенерации использованных вод при закачке в скважи­ны) имеет решение задач переноса при действии системы закачи­вающих и откачивающих скважин. При этом возникает, в частно-

95

Сти, задача выяснения максимального расстояния между скважи­нами 2/о, при котором регенерированная вода без потерь посту­пит в откачивающие скважины. При наличии двух скважин — за­качивающей и откачивающей (рис. 18)—напор и функция тока описываются уравнениями:

И = (л: cos со + sin ш) —2—in (*-'о)2 + Уа ,

Время tф прохождения мигрантом расстояния 2/0 между сква­жинами по линии тока с функцией тока ф при отсутствии потока (^0=0) определяется выражением [24, 43]

KtimL ( sinф — ^ cos Ф \ — причем для кратчайшей линии тока (при ф = 0) получается

Концентрацию мигранта в откачивающей скважине можно по­лучить, интегрируя количество мигранта, поступающего по от­дельным лентам тока. Для этой концентрации с получена аппрок - симационная формула

= 0,34 ехр (- 0,0023 + 0,34 ехр (— 0,109 - Ц +

С° — с0 \ to) \ t0j

+ 1,37 ехр ЬЗЗу-j,

Где с0 и Со — соответственно концентрации мигранта в закачиваю­щей скважине и исходная в пласте [51]. В этой работе также про­анализировано влияние скорости естественного потока, причем в тех случаях, когда поток направлен по линии, соединяющей сква­жины, остается в силе формула (6.5) с соответствующей коррек­тировкой в ней величины to.

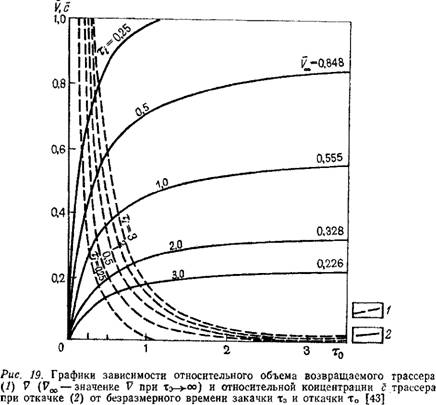
Для оценки возможностей использования закачиваемой жидко­сти интересна рассмотренная в работе [43] задача по определению количества трассера, возвращающегося в скважину при откачке, производимой непосредственно после закачки трассерного раство­ра. Численные результаты решения такой задачи позволяют опре­делить относительный объем откачиваемого трассера V (по отно­шению к общему объему закачанного трассера) и относительную концентрацию откачиваемого трассера с= (с—Со)/'(с°—Со), где с о, с0 и с — концентрации трассерного вещества соответственно в плас­товой, закачиваемой и откачиваемой воде, в зависимости от режи­ма закачки и откачки. На рис. 19 приведены графики зависимости V и с от безразмерных значений времени закачки T3 = 2nqo2tjnomQ3 и откачки To = 2nqi$t/nomQ0 при Q3 = Qo-

Подробное рассмотрение таких задач, а также для водозабор­ных скважин вблизи рек (границ первого рода) приведено, напри­мер, в работах [8, 12].

При поступлении мигрантов путем инфильтрации на поверх­ность фильтрационного потока, что характерно для условий за­грязнения грунтовых вод, необходимо оценить" их конвективный перенос не только по направлению, но и по глубине потока. Вер­тикальный конвективный перенос возникает при налйчии верти­кальных скоростей фильтрации, обусловливаемых прежде всего

97

Структурой потока, а также различием плотности загрязняющего раствора и грунтовых вод.

Для оценки конвективного переноса по глубине потока рассмот­рим условия стационарного одномерного в плане потока с постоян­ной проводимостью, пренебрегая различием плотностей фильтру­ющих жидкостей и считая фильтрационный поток плановым и жестким. Из уравнения неразрывности получим выражение для вертикальной скорости фильтрации:

Где w — интенсивность инфильтрации на свободной поверхности (при г=0).

Для однородного по вертикали планового потока предполагает­ся обобщенная предпосылка Дюпюи—Форхгеймера о постоянстве горизонтальных скоростей фильтрации vx по вертикали, т. е. vx~q/m (где q — удельный расход потока). Поскольку dqjdx =ш+ши, то выражение (6.5) примет вид vz—w—(ш+шн) (z/'m). 98

Уравнение кинетики погруже­ния при этом согласно уравне­нию (4.2) имеет вид:

Dz, . . z

Пй — - = v = w„) —- .

At tz tn

(6.7)

При постоянных значениях ш и wн, разделяя в этом уравнении переменные и проведя интегри­рование, получим

W 4" WR

Где At— расчетный интервал времени; г0 — ордината начального положения мигранта (рис. 20).

На участке с постоянными значениями w и w„ из балансовых соображений следует также соотношение

% (z0lm) + w(x — лг0) _ г

Яо + + wn) (х — лг0)

Которое связывает расстояния горизонтального и вертикального продвижения мигранта.

Аналогичные преобразования можно сделать для горизонталь­но-слоистого потока, когда коэффициент горизонтальной фильтра­ции kx зависит от z. В этом случае предпосылка планового потока формулируется как условие постоянства горизонтальных градиен­тов напора в каждом сечении, т. е. vx—kxIx=kx(qjT), так что

Kx dq kx (w + wH)

T dx

Где q и T — удельный расход и проводимость потока. Подставляя это выражение в уравнение (6.6), получим

— J kxdz = w — (w - f - ,

Tz = \kxdz.

0

Уравнение кинетики погружения мигранта (6.7) при этом имеет вид

Dz, , ч Т,

At J

Разделив пласт по проводимости на интервалы Azt с постоян­ными значениями коэффициента фильтрации ki и пористости n0h запишем для времени Att прохождения 1-го слоя выражение

Д£ — "idz

I (w 4- wH) ki bZi

WT — (w + wH) Ti_і

Где - Ті-і — проводимость пласта выше расчетного г'-го слоя. Вместе с тем из балансовых соображений запишем для сечения х соотно­шение

+ ® д*/ = [д0 + + WH) д.*,]

Или

______________ f.

W — (w + wH) Ti-\ T ' T

Рассчитав перемещений мигранта в пределах каждого і-го слоя, можно определить время достижения мигрантом любого рас­четного сечения.

При внедрении в водоносные пласты значительных потоков по­вышенной плотности на форму границы раздела между вытесняю­щей и вытесняемой жидкостями (загрязняющая и пластовая вода) существенное влияние может оказывать различие их плотностей. Для оценки этого фактора рассмотрим задачу о формировании границы раздела в напорном фильтрационном потоке между со­вершенными бассейнами, причем из питающего бассейна, начиная с момента времени ^=0, в пласт, содержащий жидкость с плотно­стью ро, поступает жидкость с плотностью р; пласт считается одно­родным, а поток стационарным. Для однородного пласта решение этой задачи получено для двух предельных случаев вертикального коэффициента фильтрации пласта kz (предполагая, что реальные условия пласта укладываются между этими случаями): для гори­зонтально-слоистого пласта (kz=0) и предпосылки Дюпюи (kz->oo).

В обоих случаях оказывается, что граница раздела имеет фор­му наклонной прямой, длина (проекция) которой описывается за­висимостью

/р=х]ЛїА, = (6.8)

Причем коэффициент х меняется от 1,41 при kz=0 до 2 при kz->oof так что для практических расчетов можно принимать среднее зна­чение х= 1,7. 100

При различии вязкостей р,0 и р, вытесняемой и вытесняющей жидкостей решение для горизонтально-слоистого пласта (Јz=0| дает уравнение

, Др т. (, , Д, и IK \ k Д|х Т,

/ =-LTln 1 + 4---------------- L=-------- р gft,

Д|л I V Ар т!

Где Ар=(р—цо)/цо; І — градиент напора пресных вод (т. е. напо­ров, приведенных к плотности пресных вод); k — коэффициент про­ницаемости.

Для практических расчетов можно представить это уравнение в форме

/р —" //pj

Где /р определяется по формуле (6.8); 7— поправочный коэффи­циент, учитывающий различие вязкостей жидкостей, причем зна­чения 7 определяются по следующим данным:

/ 2kt

Дц/І/ ... —1,5 -1,0 -0,5 0 0,5 1,0 1,5

У п0тАр

............................. 0,57 0,7 0,82 1,0 1,17 1,35 1,55

Для проверки этих зависимостей были проведены опыты на ще­левом лотке с глицерином, на основе которого добавлением хло­ристого цинка создавались жидкости с различными гидродинами­ческими свойствами, причем относительная плотность Ар менялась от —0,06 до +0,14, а относительная вязкость Ар, от —0,3 до -|-0>0& Результаты опытов показали, что величина % колеблется от 1,6 до 1,8, что подтверждает правильность приведенных расчетных за­висимостей.

Заметим, что расчетные зависимости для вытесняемой и вытес­няющей жидкостей, по-видимому, можно использовать также для учета фильтрационной неоднородности пласта, если его проницае­мость меняется по глубине примерно по линейному закону. В этом случае влияние переменной проницаемости можно считать эквива­лентным фиктивному различию вязкостей Арк;

Л^к = (^под — HkKp)!kcp,

ГДЄ Кпод, &кр И &ср — коэффициенты "фильтрации соответственно в подошве, кровле и средней ча. сТи пласїа.

В случае фильтрации воды повышенной плотности из несовер­шенного водоема, когда фильтрационный поток из водоема (хра­нилища) значительно превышает естественный поток в этом ство­ре, осложняется картина потока непосредственно вблизи водоема, где происходит резкий поворот потока. На рис. 21 показаны поло­жения границы раздела жидкостей при фильтрации из открытого хранилища в бассейн грунтовых вод, полученные на щелевом лот­ке. В этом случае граница раздела, имевшая в начале довольно сложную форму, поворачивается и вблизи хранилища (на рас-

Рис. 21. Фонограмма положения границы раздела между жидкостями различ­ной плотности при фильтрации из несовершенного бассейна по данным опытов ■ щелевом лотке.

T—5 — положения границы раздела (цифры в кружках) Я свободной поверхности. Сплошная линня — свободная поверхность, пунктир — граница раздела

Стоянии порядка двух мощностей пласта) приобретает примерно вертикальное положение. В дальнейшем характер движения гра­ницы раздела совершенно аналогичен тому, который наблюдается в напорном потоке.

Учет обменных процессов. Учет сорбционной емкости пород при равновесном протекании сорбционных процессов (без влияния Ки­нетики сорбции), как указывалось выше, осуществляется заменой в расчетных зависимостях активной пористости по на эффективную яэ, определяемую выражением (5.4).

Несложно учесть также деструкцию мигранта, когда диффе­ренциальное уравнение процесса принимает вид

Де, дс, ^ г.

А------ v--------- 1с — w — О,

Dt dt п

Где X — параметр деструкции (распада); w — интенсивность рас - иредельного поступления мигранта. Это уравнение решается при краевых условиях с(1, 0)=с0 и с(0, t)=c°. Применяя к уравне­нию (6.9) преобразование Лапласа, после обратного перехода по­лучим искомое решение:

(6.10)

Где 6=1 при t>nQl/v и 6=0 при t<.n0l/v.

Пользуясь уравнением (6.10), можно оценить возможности при­менения упрощенных вариантов расчетов по схеме поршневого вы­теснения (при Я=0, w~0), по стационарному режиму (при dc/dt — О) и без учета переноса (v — 0).

Значительно более сложно учитываются обменные процессы при миграции многокомпонентных растворов, характер переноса которых определяется не только индивидуальными термодинамиче- екими параметрами среды и мигрирующих компонентов, но и усло­виями взаимодействия этих компонентов в ходе физико-химиче - ®ких превращений. Такое взаимодействие проявляется прежде все­го в виде взаимозависимой сорбции, когда насыщение породы од - дим из компонентов контролируется равновесными содержаниями в растворе и в поглощенном комплексе других компонентов, а так - 602
же в форме образования компонентами комплексных соединении, с переменными физико-химическими параметрами.

При взаимозависимой сорбции компонентов В. Г. Румынии предлагает следующую систему расчетных зависимостей. Система уравнений переноса вдоль линии тока записывается для каждого і-го компонента: дсі, дс[ . dN[

(6.11)

Dt dl dt

Если равновесная сорбция подчиняется обобщенной изотерме Ленгмюра (3.6), то исключение из уравнений производной dN/dt позволяет представить систему (6.11) в виде

Где m — номера всех компонентов, кроме t'-го.

Нахождение аналитических решений системы (6.12) затрудни­тельно. Вместе с тем определенные характеристики межфазового взаимодействия могут быть получены из анализа частных балан­совых соотношений, вытекающих из такой постановки задачи.

Очевидно, что различия в параметрах сорбции различных ми­грантов обусловливают разные скорости перемещения этих компо­нентов в пласте, приводя к формированию подвижных зон, из ко­торых каждая ниже расположенная по потоку содержит на один сорбирующийся компонент меньше, чем предыдущая (рис. 22); общее число k-x зон соответствует числу компонентов т. Так как изотермы сорбции (3.6) всех компонентов выпуклые, то грани­цы зон испытывают тенденцию к сжатию, т. е. являются прямо­угольными. Скорости перемещения границ и„к определяются ин­тенсивностью поглощения наиболее сорбируемого в соответствую­щей k-й зоне компонента (его номер 1 = 6+1, см. рис. 22) и зависят от те­кущих значений концен­трации мигрантов в рас­творе cmkt Ckm-1, Ckk+1 и на породе Nmkr Nkm-1, • • Nkk+\. По ходу процесса наиболее активно сорби­руемые компоненты, дви­жущиеся с минимальны­ми скоростями, частично вытесняют из поглощен­ного комплекса породы n 00 v, ,

Г ^ Рис. 22. Характер зональной дифференциации

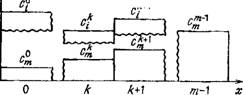
Ранее сорбированные компонентов в потоке подземных вод при их компоненты С меньшими взаимозависимой сорбции на породе

Энергиями поглощения, что может обусловливать увеличение кон­центраций последних от зоны к зоне.

Отмеченные особенности зональной равновесной сорбции позво­ляют составить элементарное балансовое соотношение для скоро­сти ипк переноса для границы любой £-й зоны:

VckM = и\ / n0ckk+l

Где второе слагаемое отвечает величине сорбционного поглощения &+1-го компонента при наличии в растворе других компонентов. Таким образом, скорость миграции компонентов на границе любой из зон контролируется ее эффективной емкостью

Kk+Л,

Аэк = п0 +

1+ 2 KiCtk /=£+1

Для расчета концентрации скі можно воспользоваться системой уравнений

J^L (і ц_ у к с k~x \ / ^І1—

КЛ п А " ) 1+ s к** і + \ /-Й+1 »=> 1

Имеющей реккурентный характер: для ее решения достаточна ин­формация об исходном составе раствора с0, поступающего в пласт.

Например, для условий миграции двухкомпонентного раствора получены следующие значения эффективной емкости:

Tij — п0 -[- ---------------- ; n9l^n0 + —

0 1 + Км* + W 9 ° l +

Где концентрация второго компонента в передовой зоне определя­ется по формуле

4х = с»,2 - Кхг + [(*°12 - Кп? 4- 2 КпС2°] V.; = 0,5 (с, о 4- с20)-

Подобным образом — в расчетных емкостных параметрах сре­ды — можно учесть влияние процессов внутрифазового комплексо - ©бразования на интенсивность нелинейной сорбции. Для начала рассмотрим условия миграции металла Me і (суммарная концент­рация стм^ в составе растворов, содержащих лигандные группы Lj (суммарные концентрации Предположим, что комплек-

Сообразование протекает по схеме, описываемой уравнениями |2.18) — (2.22), так, что концентрация свободных ионов металла eMl, принимающих участие в сорбции, всегда меньше концентра­ции cjj; считаем также, что комплексные соединения и свобод­ные лиганды не сорбируются на породе.

Очевидно, что миграция такого многокомпонентного раствора приводит к формированию двух зон: приграничной зоны исходного раствора, содержащего все комплексы (2.18) — (2.22) и ион Me і Ш4
и фронтальной зоны, обедненной ионами Mei и комплексными соединениями этого металла. Скорость миграции передово­го фронта определяется истинной скоростью движения под­земных вод и контролируется активной пористостью По. Для определения скорости щ продвижения границы зоны исходного раствора запишем уравнение баланса массы компонента Мех в этой зоне:

Где суммарная концентрация стМх определяется первым выраже­нием (2.24) при І—1, величина Ni — изотермой (3.6) (также при i=l). Отсюда получаем выражение для эффективной емкости:

+ . (6. Щ

Физически это означает, что в случае комплексообразования ем­кость пород уменьшается по сравнению с предельным случаем в (l-f-Bc>) раз за счет донасыщения породы компонентом в процессе распада комплексов металла на фронте исходного раствора.

В качестве примера проведем оценку условий миграции жестких сточных вод существенно сульфатного магниевого состава. По данным химических ана­лизов стоки характеризуются суммарным содержанием магния =400 мг|л

(1,65-10-2 моль/л) и сульфатов «£=,800 мг/л (8,33-10-3 моль/л), Рн раство­ра 5. Параметры сорбции ионов магния (Mg2+) на породе: ЛГо=5-10-2 моль /я: Жі = 102 л/моль (изотерма Ленгмюра); активная пористость породы п0—0,3. В соответствии с выражением (5.3) эффективная пористость породы без учеиа комплексообразования (при Вс=0) будет я8і—2,19.

Между тем ионы Mg2+, вероятно, участвуют в реакциях комплексообразова­ния, протекающих в данном случае по схеме

Mg2+ + S042-=^MgS04°, (Кга1) Mg2++(OH)~**Mg(OH)+, (К„он)

So42-+h+^hso4- (х2,н)

S042+2H+**H2S04°. (К22н)

Концентрационные константы представленных равновесных реакций рассчи­тываются по известным значениям стандартных свободных энергий этих реак­ций (см. гл. 2): /С, а, = 229,61; Я,,ОН = 380,19; /Смн = 80,54; /Сан = 1,0. Для рас­чета содержания ионных форм миграции элементов воспользуемся системой уравнений (2.24)—(2.26), где для рассматриваемого случая ({=1, / = 2): BCi=^11OH. IO-(14-PH)+^12iC2. BCs =/(2,Н. Ю-рн_[_Д"22Н. iO-2pH. j_/(]2lCl

Решая эти уравнения при различных значениях рН, получаем: Вс =0,43; r,== 1,16-10-® моль/л (рН 2); Вс i = 1,44: ci = 6,8-10"J моль/л (рН 7); Вс=4,99;' ci = 2,8-10~3 моль/л (рН 12). Соответствующие значения эффективной пористо­сти составляют: 1,92; 1,52 и 0,96. Из этого примера видно, что комплексообра- зование заметно увеличивает интенсивность массопереноса в водном пласте, при­чем диапазон изменения расчетного параметра пя контролируется величиной рН исходного раствора.

В принципе по аналогичным схемам может быть учтено комп - лексообразование в некоторых частных процессах ионообменной сорбции. Однако в общем случае эффективность подобного под­хода ограничена ввиду сильной зависимости формы изотермы от степени комплексации обменивающихся ионов: изменения концент-

Ros

Даации ионов-лигандов в растворе могут приводить не только к из­менению крутизны изотерм, но и к смене их форм — с выпусклой на. вогнутую и наоборот.

Процессы растворения и осаждения, имея кинетиче­ский характер, являются неравновесными и необратимыми. Урав­нение формальной кинетики, определяющее скорость изменения удельного содержания химически активного компонента в породе, обычно представляется выражением (3.14). В. одномерном фильт­рационном потоке совместным решением уравнений кинетики и материального баланса при краевых. условиях с(1, 0)=сн, с(0, t)=c° можно показать [7, 11], что, при достаточно длитель­ном растворении f2>t°==N0/[Ca—с°)ар] (где N0 — исходное удель­ное содержание растворяемого компонента в породе) формируют - ея три характерные миграционные зоны: 1) полного выщелачива­ния растворимых солей, в которой концентрация раствора близка к концентрации поступающих в пласт вод с0; 2) переходная — про­тяженностью (t—(t—t®) {vfrto), (где Uo—v/lrio-j-NoficH— —с0)], в которой концентрации солей растут по потоку подземных вод по закону

«р {^-Чг-)-'

Где n3=no+No/ (Сп—С°);

%) зона исходного, насыщенного до концентрации сн раствора.

Если масштабы процесса таковы, что его кинетикой можно пре­небречь (это обычно справедливо для весьма больших периодов времени и размеров потока переноса), то оправдано применение более простой расчетной схемы поршневого вытеснения для экви­валентных равновесных процессов, в которой межфазовые реак­ции учитываются в эффективном емкостном параметре (эффектив­ной пористости) пэ.

Миграция растворов сложного состава, химически взаимодей­ствующих с труднорастворимыми веществами, описывается со­гласно выражению (3.15) системой уравнений

Wpfio=°; /==1> k+2....................................... (6Л4>

01 01 j j

Рассмотрим в качестве примера частный случай трехкомпо- ментной системы (два компонента фильтрующегося раствора Лі і А2 взаимодействуют с твердым веществом Л3): -{т%^з~^продукты реакции. Тогда исходная система уравнений (&.14) может быть записана в следующем явном виде:

Дсі і дс^ , А

At ol

Щ + v ~- + Поъ*Рсхс2 = 0.

В. Г. Румыниным показано, что ее решение представляется в форме:

Где c0l и Ј0lJ — исходные концентрации компонентов Ах и Л2 и фильтрующемся растворе.

Процессы осаждения и растворения солей могут протекать па­раллельно, что характер для специфических областей вблизи подвижных гидрогеохимических границ —барьеров, на которых происходит резкая смена физико-химических (кислотно-щелочных или окислительно-восстановительных) условий [11]. Важная роль гидрохимических барьеров заключается в концентрировании пере­носимых химических компонентов на фронте вытеснения из перво­начально недонасыщенных растворов по мере продвижения пос­ледних по пласту.

Пусть, например, поступающий в пласт исходный раствор, со­держащий в форме диссоциированных ионов и комплексных сое­динений тот или иной химический элемент (например, металл Ме%, двигаясь по водоносному пласту, вступает в химическое взаимо­действие с минеральным веществом. Это приводит к тому, что кон­центрация активных компонентов, с которыми элемент Me нахо­дится в растворе в равновесии, падает по потоку, снижаясь до фо­новых значений на фронте вытеснения. При этом вблизи фронта происходит смена физико-химических показателей системы (на­пример, параметров рН или Eh), влияющих на устойчивость в ра­створе соединений прослеживаемого элемента Me. Учитывая, чте скорость движения активного растворителя, постоянно расходуе­мого на химическое взаимодействие с породой, всегда ниже скоро­сти миграции элемента Me, последний, опережая фронт, выносится в область пласта, содержащую фоновые воды с отличающимися от исходных растворов физико-химическими параметрами. В резуль­тате вынужденной потери миграционной способности элемент Me вблизи фронта вытеснения выпадает в осадок. Однако по мере вы­щелачивания минеральных солей (их содержание в породе счита­ется ограниченным) активность растворителя вблизи гидрохимиче­ской границы возрастает, и в раствор вновь переходит ранее осаж­денный элемент Me, причем его концентрация в растворе стано­вится более высокой. Предельное максимальное содержание эле­мента в растворе лимитируется значениями концентрации насы­щения срн, являющейся рассчитываемой константой внедряющего­ся в пласт раствора. Равновесная концентрация элемента сосн в фоновых водах, которая контролирует интенсивность высаждениж элемента, также достаточно надежно оценивается термодинамиче­скими методами. Количественный анализ таких процессов рассмат­ривался в работе [11].