Моделирование миграции подземных вод
Микродисперсия в пористой среде
Микродисперсия представляет собой рассеивание границы раздела между смешивающимися жидкостями на молекулярном и внутрипоровом уровнях.
На молекулярном уровне микродисперсия обусловливается процессом молекулярной диффузии, которая создает поток мигранта, описываемый законом Фика;
Vd= — £>м grade, (4.3)
Где Vd — плотность диффузионного потока (количество вещества^ диффундирующего через единичную площадь потока в единицу времени); Ъи — коэффициент молекулярной диффузии; с —концентрация мигранта [5]. Для песчаных пород
(4.4)
Где % — параметр, характеризующий извилистость путей фильтрации в пористой среде (по опытам Д. Клинкенберга для несцементированных песков х=0.5—0,7, а для сцементированных 0,25— 0,5); Z>m° — коэффициент молекулярной диффузии в свободной среде, имеющий порядок 10"4 м2/еут [7,33, 37].
|
(4.5) |
В глинистых породах диффузионный поток осложняется торможением диффузии в пристенных слоях жидкости за счет уменьшения подвижности ионов в двойном электрическом слое и большей вязкости структурированных жидкостей пристенных слоев [29,37]. В этом случае в выражение (4.3) следует вводить поправочный коэффициент тім, считая, что
Dm = Х^м^о^м0,
Причем по данным И. А. Брилинг для бентонитовых глин tjm==0,2, а для моренных и лёссовидных суглинков тім=0,4—0,5. ГІо данным Н. А. Окниной, Н. П. Затенацкой и И. А. Софохиной значения коэффициента диффузии для глинистых пород имеют порядок 0,1 ем2/сут или 10~5 м2/сут,[37]. Вместе с тем величина Du может существенно уменьшаться при уплотнении пород, например, по данным Г. Ю. Валукониса для аргиллитов при давлении 35 МПа получены величины £>м порядка Ю-8 м2/сут. При неполном во до - насыщении пород величина DM существенно зависит от влажности;
Например, при диффузии ^Sr в воздушно-сухой почве при объемной влажгіости 1,5% DM=2-10~9 м2/сут (по М. К. Мельниковой и В. М. Прохорову).
Заметим, что закон. Фика в форме (4.3) справедлив для изотермических процессов и при независимой диффузии; последнее допущение строго обосновывается для смесей, состоящих из двух веіцеств или содержащих избыток одного из компонентов, а также при одинаковых коэффициентах диффузии всех компонентов смеси. При невыполнении этих условий возникают более сложные явления неизотермической многокомпонентной диффузии [11].
Молекулярная диффузия сопровождается осмотическим переносом, который представляет собой встречное перемещение растворителя (воды), равное диффузионному по величине и противоположное по направлению. Выражение для плотности осмотического переноса воды оОСм имеет вид [29]г^см ==—£)осмgrade; Ajcm = DMl — (1 — [3) Dm; p = dpldc, где DOCM — коэффициент осмоса; DMl и Dm—парциальные коэффициенты молекулярной диффузии растворенного вещества и растворителя соответственно. В частности, для водного раствора NaCl имеем Ј>Mt = 1,61 - Ю-5 см2/с и DM,==1,93.10-5 см2/с,■ р=0,7, т. е. />ОСм= (1,61—0,7-1,93) X XI О"5 см2/с= 1,03* 10~5 см2/с.
Для характеристики осмоса используется понятие высоты осмотического давления Лосм, которое эквивалентно по условиям переноса пьезометрической высоте столба воды. Тогда выражение для Оосм записывается в виде, аналогичном закону Дарси:
*>осм = — Р& grad hocu, (4.6)
Где k — коэффициент фильтрации.
Сопоставляя выражения (4.6) и (4.1), можно видеть, что перепад высоты осмотического давления Ahpcм связан с перепадом концентрации растворенного вещества Ас соотношением
Рkh0CM = D0CM Дс или ДЛ0СМ = — ,
К р
Из этого выражения видно, что перепад осмотического давления сильно зависит от проницаемости пород, поскольку перепады, концентраций в подземных водах имеют сравнительно небольшие пределы изменений, а величины D0CM и р практически постоянны.
Приведем пример расчета величин Моем Йри Ас = 50 г/л, р = ==1000 г/л и />осм=Ю-5 см2/с. При характерном для глинистых по^од значении Ю-5 м/сут=10-8 см/с получим
Д^осч == —0_g * "jqqq ~ см> а Для песчаных пород при &=10~3 см/с получим. Дйосм =5-10~4 см. Из этого прймера видно, что осмотический перенос может заметно проявляться лишь в весьма слабопроницаёмых разделяющих пластах, где с этим фактором следует считаться.
Поскольку «любая форма движения способна и вынуждена <...> превращаться, прямо или косвенно, в любую другую фор-
|
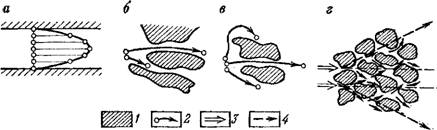
Рис. 9. Схемы образования гидродисперсии [8, 37] за счет неравномерности поля скоростей в поровом канале (а), различия скоростей в различных поровых каналах (б), деформации линии тока в поровом пространстве (в),, поперечного рассеивания (г). /—зерна породы; 2 — локальные лнннн тока; 3 — направление потока; 4.~ конїур поперечной дисперсии |
Му движения» [6], потоки мигранта создаются также всеми физическими полями. Однако их практическое влияние имеет обычно весьма ограниченный характер.
В приповерхностной (почвенной и подпочвенной) зонах при значительных колебаниях температуры может проявиться термодиффузия, создающая поток массопереноса под действием градиента температуры плотностью Vta=—D*grad9, где Dt —коэффициент термодиффузии, причем в рыхлых породах Dt — 2Х XIО"5 см2/(с-градус) [17].
В электрическом поле возникает элёктроосмотический перенос под действием градиента электрического потенциала» Практическое применение электроосмотический перенос находит при электроосушении глинистых пород, а в естественных электрических полях его влияние обычно незначительно.
На больших глубинах может проявляться эффект бародиффу - зии, заключающийся в разделении более и менее тяжелых компонентов водного раствора под действием градиента давления [34].
На диффузию микроорганизмов может также накладываться хемотаксический перенос, который представляет собой собственное движение микроорганизмов в направлении участков с более высокой концентрацией необходимых им питательных ве-^ ществ. Ф. Далквист [52], изучавший миграцию бактерий Sallmo - nella typhoimurium в растворе аминокислот, предлагает описывать, плотность хемотаксического переноса ухт зависимостью от концентраций спв питательных веществ вида vxr = kxrA In спв = = (&xT/CnB)gradc„B, где kXT — хемотаксический коэффициент, который может считаться в определенных условиях постоянным.
Неравномерность поля скоростей в поровом пространстве создает статистические отклонения скоростей переноса отдельных частиц по отношению к средней действительной скорости течения, что приводит к образованию гидродисперсии (рис. 9). Многочис ленными экспериментальными исследованиями показано, что продольная гидродисперсия (по направлению потока) описывается законом Фика (4.3), в котором DK заменяется на коэффициент продольной гидродисперсии Di, зависящий от скорости фильтрации. В частности, по результатам лабораторных опытов Г. Пфан - куха для однородных песков получается [37, 74]:
А = А, + \v при 8, ^ 1М, (4.7)
Где d — средний диаметр зерен.
Д. Харлеман, П. Мельхорн и Р. Румер предлагают зависимость для Di в виде
А — 88/?к1'2; А = A/(%v); RK = vVklM, (4.8)
Где v — коэффициент кинематической вязкости; к — коэффициент проницаемости. Эта зависимость экспериментально обоснована для песков с k= 10~6~ 10"5 (d50 = 0,45—1,4 мм) при л0 = 0,39.
Вместе с тем обобщение и анализ всех экспериментальных данных [46] указывают на возможность использования для песчано - гравийных пород нарушенного строения зависимости (4.7) при; бі =0,63 мм.
По данным полевых опробований, проведенных Д. Биггаром и Д. Нельсоном [90], в уравнении (4.7)
8,-2,93 (v/fio)0'11, (4.9)
Где при и, измеряемом в сантиметрах в сутки, получаем бі в сантиметрах. Это выражение дает значительно большие величины параметра гидродисперсии, чем определенные в лабораторных условиях.
Для агрегированных пород Д. Пассиура [90] представил выражение для Di в форме
А = Du + М + 8, 82«ід, (4.10)
Где ел — относительное содержание агрегатов; йк — диаметр агрегатов; Da — коэффициент молекулярной диффузии в агрегатах [7]. Это выражение хорошо согласовалось с некоторыми экспериментальными данными [74].
При неодномерном потоке переноса возникает также поперечная дисперсия, создающая плотность поперечного потока мигранта —по нормали к направлению фильтрационного потока, определяемую законом Фика, в котором £)м заменяется на коэффициент поперечной дисперсии Dr.
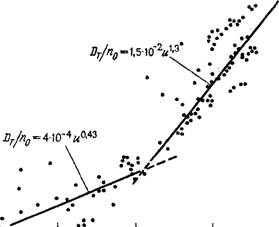
Экспериментальные данные, представленные в различных работах, нанесены на график (рис. 10), где проведены рекомендуемые
10 г---------------
|
|
|
10-3 |
|
10-з |
|
10"2 |
|
Рис. 10. Сводные данные экспериментального определения коэффициентов поперечной дисперсий4 [44] |
|
Ю-4 |
|
10"5 |
|
10"4 |
|
КГ1 |
|
10° |
|
И - v/riQ, см/с |
|
(4.11) |
Аппроксимационные зависимости [44]. Учитывая значительный разброс экспериментальных точек, удовлетворительную их аппроксимацию можно также представить более простым выражением:
А = DM + 8тг>,
Где бт — параметр поперечной дисперсии, бт — 0,06—0,2 мм.
Численный анализ показывает [36], что продольная гидродисперсия в гомогенных пористых средах обычно не играет сколько - нибудь существенной роли при массопереносе в подземных водах, заметно проявляясь лишь в лабораторных опытах. Значительно большее влияние в натурных условиях оказывает макродисперсия, обусловленная макронеоднородностью строения горных пород, имеющей размеры порядка 0,01—1 м.