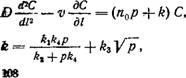Моделирование миграции подземных вод

Конвективно-дисперсионный перенос в одномерном однородном фильтрационном потоке

Приведем наиболее часто употребляемые аналитические решения и способы их получения для переноса однокомпонентного мигран­та с учетом процессов дисперсии в гомогенной и гетерогенной сре­дах.

Линейный перенос. Для линейного переноса в направлении I жри сформулированных выше условиях в общем уравнении пере­носа (5.1) следует исключить члены поперечной дисперсии и пре­вращений, считать, что dN/dt=Kddc/dt, а член и*~и** задать со­гласно выражению (4.14). Тогда дифференциальные уравнения пе­реноса можно представить следующей системой:

(6.15)

(6.16)

Где = £3=р*; k4=я*0и* (здесь <%* и с* определяются

Согласно выражениям (4.12) и (4.14), п*0 и х*— пористость и удельное содержание блоков с сосредоточенной емкостью, причем величины По и «о* для сорбируемых мигрантов заменяются на эф­фективную пористость (емкость) породы, определяемую соглас­но выражению (5.3)). Заметим, что эти же уравнения описывают перенос в гомогенной среде при линейной кинетике сорбции [см. уравнение (3.7)]. В этом случае в уравнении (5.1) надо положить х— 1, u*=R=0, что для одномерного потока приводит к уравне­ниям (6.15) при N~c*, &1 = <%к, k2=a. K$, h—Q, &4=1.

Решение фундаментальной задачи. Фундамен­тальная задача решается для условий с(0, t) = с0, с(х, 0) =с(оо, t)=*=c*(x, 0)=с*(оо, f) = Со. Заменим в этой системе с и с* на безраз­мерные переменные с— (с—Со)/(с0—с0) и с* {с*—Со)/(с0—Со), для которых краевые условия фундаментальной задачи будут с(0, t)~ — 1, с(х, 0) — с(оо, t) =с*(х, 0)=с*(оо, t) =0. Вводя преобразо­вание Лапласа — Карсона С, С* и с/ величин с, с* и с/, прежде всего учтем, что при начальных нулевых условиях решение уравне­ния 4.14) в изображениях по Лапласу—Карсону имеет вид

А из уравнения (6.16) получается соотношение С* = ——- С.

Тогда уравнение (6.15) в изображениях будет иметь вид

(6.17)

Причем для фундаментальной задачи оно должно решаться при условиях С(0) = 1 и С(оо)—0. Такое решение имеет вид

С = e~al, (6.18)

Где а находится из уравнения a2D-{-av=n0p-{-k, откуда

JL. V2-L поР + k_____ L,

2D I D 2D

Приведем выражения оригиналов этого изображения для част­ных моделей переноса.

Для диффузионной гомогенной модели (при ki=k2=k3 = 0, ;П\ = п) решение имеет вид [7, 37, 38]

(6.19)

Где X=vl/D; Q = v*t/(noD).

Для длительного процесса применяется асимптотическое выра­жение этой функции

^(X,9)=0,5erfcS;E-^f = (6-20)

Погрешность которого оценивается величиной 0,3/ >/~0.

Для гетерогенно-блоковой среды со сосредоточенной емкостью блоков (при D = 0 и ^з=0) получено выражение [11, 30, 39]:

Е - /о + /е-/о (21ЛЙ dz

О

С = F* (yj, х) = е-ч где

■П = kil/w, x-A^-J&L). (6.21а)

/0 — функция Бесселя от мнимого аргумента. Таблица функции F*(r\, т) приведена в прил. 4. При больших значениях аргументов для этой функции можно пользоваться приближенным выражением

X)=0,5erfcC, С = (7]-т)/(2/7).

Численный анализ показывает, что это выражение при г)>4 дает погрешность по времени, оцениваемую величиной 0,55/г|. Для гетерогенной среды с неограниченной емкостью (при D = = 0, &j = &2=0) решение получил Г. Лаверье [31, 38]:

C = erfcX, Х = ——М= (6.22)

2Vv(vt — щі)' v

Причем c(l, t)— 0 при vt^.n0l.

Для гетерогенной среды с комбинированной (сосредоточенной и неограниченной) емкостью изображение представляет собой про­изведение изображений, полученных для схем сосредоточенной и неограниченной емкостей в отдельности. Применяя операцию свертки оригиналов, получим, что для комбинированной емкости

Выражение оригинала для условий фундаментальной задачи будет иметь вид t

R=Jerfcщф, t-Ae^e, X

Где г) и т получены согласно выражению (6,21,а).

Для модели с необратимым распадом переносимой примеси без дисперсии (&2=&з=0, D—0) решение имеет вид:

J при vt > nQl, при vt < я0/,

Для получения решений при совместном проявлении гидродисперсии и внут­реннего обмена в гетерогенном пласте можно использовать метод, заключаю­щийся в выделении составляющих миграционного процесса, отражающих влия­ние дисперсии и обмена в гетерогенной среде. Как отметил В. Г. Румынии [31], такой метод обусловлен однотипностью выражений для преобразований по Лапласу исходных уравнений, описывающих процессы переноса в однородной и гетерогенной средах и различающихся лишь коэффициентами при трансформанте производственной функции концентрации по времени. Действительно, из общего уравнения (6.15) следует, что для изображения концентрации с' в гомогенной среде при kl = k2=h=b можно составить уравнение

Сопоставляя уравнения (6.24) н (6.17), замечаем, что кинетические процессы в пласте при решении краевых задач могут быть учтены формальным приемом: для этого достаточно в трансформанте производной функции концентрации с' по времени заменить параметр преобразования р на сумму p+(k/na). Эквива­лентная математическая запись имеет вид:

Аналогичное решение для гетерогенной среды с неограниченной емкостью в диффузионном переносе (£1 = &2 = 0) получено В. Г. Ру - мыниным [31]:

О 3 у у З

Следуя таким путем и используя решение (6.23), получаем решение для модели с нербратимым распадом (k2—k3—0):

Ву) ехр ~~ • (6.27)

Выражение (6.24) дает стационарное распределение при t-^oo:

Ехр

Изменения краевых условий. При любом изменении граничного условия и начальном нулевом условии решение получа­ется по принципу суперпозиции при замене реального графика гра­ничного условия ступенчатым (рис. 23, а), причем для момента [Времени tn-\<.t<.tn имеем

* = c^F(t) + 2 W(t - tt), (6.28)

'-1 I

Где F(t)—решение фундаментальной задачи. В пределе — при стремлении числа ступенек к бесконечности — выражение (6.28) обращается в интеграл Дюамеля.

Для гетерогенной среды с сосредоточенной и неограниченной емкостями без учета диффузионного переноса исходные дифферен­циальные уравнения имеют первый порядок, что позволяет учесть неравномерное начальное условие по принципу суперпозиции. На­пример, для гетерогенной среды со сосредоточенной емкостью ре­шение фундаментальной задачи (6.21) записывается при c0=eonst так; c=c°-j- (с0—с°) [1— F*(t|, т)].

Для ступенчатого графика начального распределения величины €0 (см. рис. 23,6) решение по принципу суперпозиции имеет вид

С - <fi + («?м - с») [ 1 - Рщ (У1, т)] + 2 (*<>. г - C0i!_,) X

Ті - Ті,)],

Где п — число дополнительных ступеней в графике Co(l); %і и т|г — значения т и т| при l=U.

От-

Рис. 23. Ступенчатые графики зависимости изменения концентрации на границе от времени (а) и начального распределения от длины потока (б)

При задании на границе х=0 полуограниченного потока гра­ничного условия третьего рода вида c=c°-\-(D/v) (дс/ді) и началь­ном нулевом условии решение можно получить, вводя вспомога­тельную функцию

V dl

Которая удовлетворяет системе уравнений (6.15) — (6.16) и имеет те же граничные условия, что и фундаментальная задача. Выра­жая из уравнения (6.29) с через <р, как из обыкновенного уравне­ния первого порядка, получим

Оо

С = S F (z, t) dz, So = vl/D,

Где F— решение фундаментальной задачи при с(0, t) = \. Для диффузионной гомогенной модели решение такой задачи приведе­но в работе [56]; численный анализ этого решения показывает' что заметное влияние границы третьего рода проявляется при |0-<10.

Радиальный перенос. В качестве основного рассматривается случай закачки в скважину раствора с постоянной концентрацией и с постоянным расходом Q на единицу мощности пласта при ква­зистационарном режиме течения в области переноса закачиваемо­го раствора, когда исходное дифференциальное уравнение (6.18) преобразуется к виду:

Q дс дс, , дс*

—------- = Я0 --------- \- ^ -—•

2г, г дг dt dt

Решение такой задачи существенно отличается при разных фор­мах зависимости D(v). Наиболее простым является решение при квадратичной зависимости D = 62v2=82[Q/(2jir]2 и постоянных значениях остальных параметров, когда дифференциальное урав­нение для радиального потока принимает такой же вид, как урав­нение (6.15) при Q—Ь. Следовательно, в этом случае для рассмат­риваемой задачи применимы все решения линейных задач, в кото­рых только заменяется v на Q, D на &2Q2 и 1=л(г2—г2с). В част­ности, для гомогенной среды решение фундаментальной задачи при с(г, 0) —0, с(гс, f) = l И постоянном расходе Q имеет выраже­ние (6.19) при %=n(r2—r2c)Ql82 и e=Q2*/(ft062).

При линейной зависимости коэффициента дисперсии от скоро­сти фильтрации Ј)=6j [Q/ (2я/*) ] фундаментальное решение урав­нения (6.30) в изображениях по Лапласу—Карсону дается форму­лой [77]:

K\/z{z)—модифицированная функция Бесселя второго рода по­рядка 1/3. Оригинал этого изображения исследовался в работе [77]. При Z)=eonst и гомогенной среде (kl—k2—k3=0) решение такой задачи получено Н. Н. Веригиным [7] и табулировано в ра­боте [4].

Имея в виду условность структуры зависимости коэффициента дисперсии и обмена от скорости фильтрации, можно рекомендовать искать приближенное решение радиальных задач переноса, усред­няя величину r2D и k\ в уравнении (6.30) во времени и в прост­ранстве.

При усреднении во времени будем исходить из того, что дис­персия наиболее интенсивно происходит вблизи фронта поршнево­го вытеснения, где

Тогда расчетное значение коэффициента дисперсии радиально - то потока Dr определится средним интегральным значением вели­чины 4n2r2D, для которой в выражении (6.31) заменяется г на г0, что дает

Dr = 2ж2г02DM + ± *гМ + т2- (6.32)

Аналогично получим расчетное значение = в радиальном потоке при а* из (4.12):

T

К f («-• + dt = ad* + h& .

T J \ 2zr0 } кг0

О

При усреднении в пространстве можно воспользоваться сред­ними интегральными значениями по расстоянию

Г

Dr = - L Г4iz2r2Ddr = — тг2r2Du -\-izr\Q +82Q2 (6.33)

Г.) 3

О

Шли по площади

Г»

£>г — J_ J 4ir2r2Dr dr — 2tcV2Z)m + nr^Q - f - 82Q2. (6.34)

О

Выражения (6.33) и (6.24) получены при r>rc. Если это усло­вие не соблюдается, то г заменяется на г—гс. Например, для диф­фузионной гомогенной модели (при kl=k2=k3=0) решение фун­даментальной радиальной задачи при Q=const имеет вид (6.19) при D=Dr.

Для случая бг=0 приближенное решение радиальной задачи получено [8, 24] на основе преобразования в члене, содержащем коэффициент дисперсии:

Д __ 2лир/- д

Dr = Q dt

Такое решение приводит к выражению, формально идентично­му тому, которое получается при Dr, определяемом согласно (6.34).

Численный анализ приближенных решений при зависимости D — 81V показывает [8], что использование выражений (6.32) и (6.34) дает соответственно заниженные и завышенные значения с, причем они обеспечивают практически приемлемую точность для выражения (6.32) при r>106b а для выражения (6.34) при г>50бь

Диффузионное распространение вещества от точечных источни­ков загрязнения в линейном фильтрационном потоке. Рассмотрим условия точечных источников загрязнения в одномерном фильтра­ционном потоке с учетом диффузии (дисперсии), когда раепреде - 114

Использование аналитических решений для обоснования расчетной модели

Аналитические решения могут эффективно использоваться для обоснования расчетных моделей путем проведения численных экс­периментов для типичных задач.

В условиях фундаментальной задачи по длине потока форми­руются зоны вытесняющего и вытесняемого растворов (с относи­тельными концентрациями мигранта с~ 1 и с=0), между кото­рыми за счет влияния дисперсии и обменных процессов образуется переходная зона с переменной концентрацией мигранта (1>с>0). Соответственно относительное влияние процессов, обусловливаю­щих ее образование, количественно оценивается отношением 1п/1к (где /к—vt/n0 — длина продвижения фронта конвективного пере­носа; 1п — расстояние, на которое переходная зона упреждает про­движение фронта конвективного переноса). Дадим по этому отно­шению оценку различных факторов, накладывающихся на конвек­тивный перенос мигрантов.

При переносе нейтрального мигранта в гомогенной среде пере­ходная зона обусловливается влиянием гидродисперсии. При дли­тельном протекании процесса, когда решение фундаментальной задачи представляется выражением (6.20), передняя граница пе­реходной зоны обгоняет фронт конвективного переноса на расстоя­ние In, определяемое (с точностью до 0,1 %) формулой [38]

(6.41)

Относительная роль для продольной гидрОдиспЕрсии (при Di = btv) определяется соотношением lJtK — 4,4 .

Анализ этого соотношения показывает, что влияние продоль­ной гидродисперсии может быть существенным в лабораторных условиях и практически не проявляется в натурных [23, 38].

Оценку относительной роли кинетики внутреннего обмена да­дим, рассматривая решение фундаментальной задачи (6.21). Из численного анализа функции F* следует, что при больших значе­не яиях аргументов (г)>4) величину 1„ с точностью до 0,1 % можно находить из выражения

Tj-X = 4,4 УТ, (6.42)

В котором ті и х находятся согласно уравнению (6.21, а) при 1= — 1к-\-1„. В частности, для гетерогенно-блоковой среды с сосредо­точенной емкостью при &1 = &2=а*, к4=я0(1—к), щ=хп0 из вы­ражения (6.42) получаем

4 = (6.43)

Сопоставляя формулы (6.41) и (6.43), можно видеть, что они переходят одна в другую, если положить

А(6.44)

Аг

Выражение (6.44) можно использовать для формальной связи моделей гидродисперсии (диффузии) и гетерогенно-блоковой среды.

Согласно уравнению (6.43), время tR, до которого следует учи­тывать кинетику внутриблокового обмена, представится выраже­нием

4 = 20-^-, (6.45)

Где б/= (/п//к)доп — допустимая погрешность расчетов переноса.

Для песчано-глиниетых пород во внутриблоковом обмене обыч­но превалирует конвективный перенос, так что согласно формуле (4.12) в выражении (6.45) будет а* = ЯкР. Тогда в условии (6.45) удобнее сделать замену lK=vtR/n0 (где /к — длина пути конвек­тивного переноса, на котором происходит полный обмен с блока­ми), и записать его в виде

/. = 20/(ХА). (6.46)

Приведем практические оценки величин tR для карбонатных пород, принимая полученные по данным натурных определений [23, 31] значения удельной поверхности блоков s*=3—5 м-1 при Z>m=3-I0~5 м5/еут и я2=0,1. Тогда согласно уравнению (4.12) по­лучим а*=4-10~4 сут-1 и при 6/ = 0,1 из выражения (6.45) най­дем значения ^ = 4-104 сут. Оценим также длину потока h для расчетов солепереноса в супеечано-суглинистых породах, принимая на основании опытов в монолитах значения Як=(1—10) м-1 при размерах блоков 0,1—0,3 м [39]. Тогда согласно уравнению (6.46) при 6/=0,1 получим /к=16—160 м. Приведенные оценки показывают, что при размерах блоков порядка 0,1—1 м процессы кинетики внутриблокового обмена имеют существенное значение, и, как правило, их следует учитывать в практических расчетах.

Иная картина может получиться применительно к гетерогенно­сти меньших масштабов. Например, при миллиметровых размерах

117

Слабопроницаемых включений, считая, что при кубических блоках: размером /*= Ю-3 м имеем s* = 6fl* = 6-Ю-3 м3, таким же путем - найдем а*=0,5 сут-1 и 2^ = 30 сут, откуда следует, что такая ге­терогенность влияет на кинетику процесса внутреннего обмена только при рассмотрении малой длительности процесса. Из тако­го расчета следует также, что гетерогенность процесса на поровом уровне (учет иммобилизованной воды в застойных или «мертвых»- порах) не имеет практического значения для решения гидрогеоло­гических задач.

В гомогенной среде дисперсия фронта конвективного переноса может обусловливаться также кинетикой сорбционных процессов.. Если принять уравнение линейной кинетики сорбции (3.7), то ре­шение фундаментальной задачи представится выражением (6.21) при ki = aK, ^2=акр, &4=1 и tii = n0. При этих значениях парамет­ров из выражения (6.42) при /=/к+/п получим формулу

(6.47)

Судя по литературным данным [7, 38], характерные значения ак находятся в довольно узком диапазоне ак—0,1—0,5 сут-1.

Численным анализом формулы (6.47) нетрудно убедиться, что при таких значениях ак величина tn/tк, характеризующая относи­тельное влияние кинетики сорбции на процесс переноса, в лабора­торных условиях может оказаться значимой, однако в натурных условиях она обычно становится пренебрежимо малой. Следова­тельно, при гидрогеологических расчетах влиянием кинетики об­менных процессов в гомогенной среде обычно можно пренебречь.