Механика трубопроводов и шлангов

Уравнения равновесия

Как правило, под трубопроводом понимают пустотелый стержень круглого сечения. Однако в реальных конструкциях могут быть использованы и пустотелые стержни с различной формой сечения, например, эллиптического и прямоугольного се­чений (рнс. 5.1). Поэтому уравнения равновесия выведем для произвольной формы сечения пустотелого стержня, который в шльнеишем отождествляется с принятым термином трубопро­вода.

Уравнения равновесия сил, действующих на элемент стержня.

Рассмотрим отдельно элемент трубопровода (пустотелого пержня) и заполняющей его жидкости со всеми силами, дей - пвующнмн на них (рис. 5.2). Б дальнейшем будет считаться, что выполняются все допущения, которые используются при выводе уравнений равновесия и движения стержня в механике

I нбких стержней [60].

Элемент жидкости имеет скорость движения Тоо {гйо=гУоС1),

I ;е шо — осредненпая по сечению скорость частиц жидкости. Воспользовавшись принципом Даламбера, получаем уравнение

Ds

!Де Р — площадь сечения трубки; р0 — давление в жидкости; т2— масса жидкости, приходящаяся на единицу длины трубо­провода; / — распределенная сила взаимодействия жидкости с трубкой. Для идеальной жидкости вектор / всегда лежит в пло - кости векторов ёг, Рз (как в статике, так и в динамике), т. е. »ртогонален вектору Ъ. Так как скорость движения жидкости '/’» зависит от двух переменных, то полная производная по вре­мени (воспользовавшись переменными Эйлера) равна

(5.2)

Если трубопровод находится в равновесии, а скорость дви­жения жидкости постоянна (стационарный режим движения кпдкости), то dwoldt=0, и из (5.2) при F=const получаем

(5.3)

TOC o "1-5" h z Рис. 5.1 Рис. 5.2

Рассматривая элемент стержня, можно получить следующее уравнение равновесия:

F? o=0; (5.4)

Где до — внешняя распределенная нагрузка.

Исключая из уравнений (5.1) и (5.2) вектор /, имеем

Ds [(^>o-bw2‘ffi’o)^il-{-Y'l_^o=0 (5.5)

Или _

-^L+Y+^o=0[Y==(w1-fm2)il, (5.6)

Где

Qo = (СіО} — Ро Є1 -{- ^20^2 "Ь Q.30^3- (5.7)

Б выражении (5.7) <2ю(!) — полное осевое усилие в стержне с учетом потока жидкости и внешней нагрузки. Для идеальной жидкости справедливо уравнение Бернулли, связывающее дав­ление ро со скоростью жидкости Шо,

Ро + ^"~+~~=const; (5.8)

Для стержня с постоянной площадью F

Я„+~-т2щ;о-[-т2£А-2о=const (P„=p0F). (5.9)

Уравнение равновесия моментов, действующих на элемент стержня. Рассматривая элемент стержня (см. рис. 5.2), можно 36

Получить следующее уравнение равновесия (одномерный поток идеальной жидкости не создает моментов, действующих на стержень):

“ + Й X + ■ (5-10>

Где (,1о — распределенный момент, действующий на стержень. _

Так как в уравнение равновесия (5.6) входит вектор ^ ю и в уравнении (5.10) перейдем к вектору @о» воспользовав­шись равенством

Ё. хй'^^хёо, (5.11)

I. е. уравнение (5.10) может быть записано в виде

-^-+(ё1хО„)+Й®=0. (5.12)

Следует отметить, что запись уравнений равновесия в форме

(5.6) и (5.12), когда действие потока жидкости учтено в вве - 1.сн1юм век горе @о, совершенно необязательно.

Слагаемые с Р0 и можно и не объединять с вектором @0(|)» •.то приводит к уравнению (5.5), которое совместно с уравне­нием (5.10) дает систему уравнений равновесия стержня.

Общие векторные уравнения равновесия трубопровода. В наи­более общем случае на трубопровод могут действовать сосредо­точенные силы Р{ и моменты приложенные в разных сече­ниях (рис. 5.3). Сосредоточенные силы и моменты можно учесть и уравнениях (5.6) и (5 12), воспользовавшись функцией Дира­ка (б — дельта-функция), что приводит к следующим общим уравнениям:

-^ + У + ?о+]Р(‘,8(»-«/) = 0; (5.13)

— _ _ _ Р

-~Ч(*1Х + »>8 (*-*,)=0. (5.14)

Для статически определимых задач, когда равновесная фор­ма трубопровода практически не отличается от исходной нена - Iруженной (в_этом_случае С](5)~ёю — известная функция), для определения Со и Мо достаточно уравнений (5.13) и (5.14).

На рис. 5.4 показаны сосредоточенные силы, представляющие собой реакцию потока жидкости в местах резкого изменения направления движения, например, в местах, где участки трубо­провода стыкуются под некоторым углом 2р. Воспользовавшись

Рис. 5.3

Теоремой о изменении количества движения жидкости (и учи­тывая силы Р от давления в жидкости), получаем следующее выражение *ля модуля сосредоточенной силы PKW (рис. 5.4):

|P(K)|=2P0cos p-j - 2т&воcos (P0-j - т2ъ%) sin. (5.15)

Направление силы P[-l) показано на рис. 5.4. Сосредоточен­ные и распределенные силы, вызванные потоком, нагружают трубопровод; на криволинейных участках трубопровода возни­кают распределенные силы, равные тг^о2хз, где — кривизна осевой линии стержня.

Вызванное потоком жидкости начальное напряженное со­стояние трубопровода существенно влияет на его частотные характеристики, что при исследовании задач динамики следует обязательно учитывать. Полученные уравнения равновесия

(5.13) и (5.14) справедливы как для случая, когда форма осе­вой линии трубопровода при нагружении внешними силами практически остается без изменения, так и для случая, когда форма равновесия при приложении внешних сил существенно отличается от исходной (например, для трубопроводов с малой жесткостью). В первом случае вектор ё, входящий в уравнение

(5.14) , есть известная функция координаты s с известными про­екциями в декартовых осях; во втором случае вектор ё, иенз - вестен, и для определения Qo и Мо уравнений (5.13), (5.14) не­достаточно, поэтому для решения задач статики необходимо рассматривать деформации трубопровода.

Уравнение, связывающее М и и. Как известно, при упругих деформациях стержня (в пределах закона Гука) внутренние моменты связаны с приращениями кривизн соотношениями

М01=Ац (xj — *10); Ж02=/22 (х2 v.2q); М03—Л33 (х3 — или) (5.16)

Где А\ — жесткость трубопровода при кручении; Л22 и Лзз — жесткость трубопровода при изгибе относительно главных осей.

В уравнение (5.17) входит вектор

*0 * = У-ігА Н-*20є2'{~%‘^3 (5.18)

В то время как для стержня в неиагруженном состоянии вектор /а1* (в базисе {ё, о}) равен

'х0 — *10^10к20е20 ~Ь у-юезо - (5.19)

Надо иметь в виду, что

(5.20)

Введенный вектор 41} имеет проекции в базисе {ег} (базис {<т,} связан с деформированным состоянием трубопровода), равные проекциям вектора щ в исходном базисе {ёго} (до на­гружения стержня силами). Упругие моменты, возникающие в стержне (компоненты вектора Мо в базисе {с*-}), пропорциональ­ны приращению кривизн, которые должны быть представлены в _іом же базисе, что приводит к необходимости введения вектора /!') (5.18)

Уравнение перемещений точек осевой линии стержня. Из

{ЛІС. 5.5 следует г—г0=й, где «— вектор перемещений точек осевой линии стержня. Дифференцируя її по 5, получаем урав­нение

~=є1~ет=—(Іп~)е1 — І2хЄ2—1^е. у (5.21)

Уравнение, связывающее вектор х с вектором А1

; = £-+Ло’- (5.22)

В результате получаем си­стему уравнений (5.13), (5.14),

(5.17), (5.21) и (5.22) (совме­стно с матрицами Ь{ и Ь), со - держащую пять векторных не - в «постных: 5о, М0, х, ■& и й. По­лученная система уравнений справедлива для любых пере - Рис. 5.5
мещсний трубопровода при условии, что материал трубопровода работает в пределах закона Гука.

Приведение уравнений к безразмерной форме. Наиболее удоб­ными при решении на ЭВМ являются уравнения, приведенные к безразмерной форме. Это можно сделать, приняв

£=1в', Qo==Q^)Aзi/l2^ к=у.//; /И0=А/!0А33/1; <7о==*7о-^яз1 /№’, |^о==

=Мзз/*2; У=ЪАуР-, А„=А„/А^ РМ=Р(ПА33/Р-, ЭД(0 =

=Й(,,Лзз//.

После преобразований для стержня постоянного сечения по­лучаем следующую систему уравнений в безразмерной форме (значок тильды в безразмерных величинах опущен):

^+й)+?о+>^“>Че-е ,)=0; -^+(ё, хад+р0+

1

|Мп

Л1,~А ('/-*["); Л = 0

II О

Ь(^11 1) с На^г I -0:

;=л, %.+£$'.

(к

Компонента <7Ш безразмерного вектора

VI. имеет вид

.

Слагаемое, содержащее се'о, можно упростить, введя безраз­мерную скорость:

■ю0=ж!0гр0 (р0= (5.29)

Где ро — величина, имеющая размерность частоты. Во втором разделе книги, по­священном дниамике, рас­сматриваются ураънення движения, содержащие раз­мерное время которое свя­зано с безразмерным вре­менем т (один нз возмож­ных вариантов перехода к безразмерному времени) со­отношением (=ро%.

Ош-=йг)-рп+

После преобразований соотношения (5.28) получаем выра­жение для безразмерной компоненты фю (значок тильды нап безразмерными величинами опущен):

1^1) (п,- —(.5.30)

тг + /п-2 }

Следует отметить, что из уравнений (5.23) — (5.27) как част­ный случай (при Ро~П — 0) могут быть получены уравнения стационарного режима движения гибкого стержня сплошного сечения (рил 5.6).

§ 6. Уравнения равновесия трубопровода в связанной системе координат

Векторные уравнения равновесия в связанной системе коор­динат. Чтобы получить уравнения равновесия в проекциях на координатные оси (в скалярной форме), необходимо предста­вить векторы в соответс1вующем базисе, например, в базисе, связанном с главными осями сечения. При этом надо иметь в виду, что от е зависят не только проекции соответствующих век - юров, но и единичные векторы базиса г{ (е). Воспользовавшись формулой (3.24), перейдем в уравнениях (5.23)—(5.26) к ло - к а л Ы1 ы м производным:

TOC o "1-5" h z -§4-* Р(,,8(в-е1)=0; (6.1)

^ +~* X Ж0 + ё, X ёо+Ро + ^ «ДО 8 (в~ Е)е = 0; (6.2)

(-*Хд +(/„ 1)^1 —{— ^21^2 —^ 31^3 0. (6.3)

5=/-! — +^1); (6.4)

М^А (6.5)

Уравнение (6.1) можно записать со слагаемым, зависящим >г потока жидкости в явном виде, г)пт,

—Е ([(^о+лл)] ^)-Ь*хд£°-хх [(Я0+«1®?) У+

Ч~ Уо~г? оН~^^>(<)^(е —е,)=0. (6.6)

Уравнения равновесия, когда деформации стержня можно считав малыми. В этом£лучае в уравнениях равновесия (6.1) —

(6.5) можно считать и * цто приводит к следующим уравнениям (знак тильды в обозначении локальной производной опущен):

^ + х(7г +Т,+?,+Уя1!)*(«-е,) -0; (6.7)

* п

]Й0хёихУ„ + Г‘о-г -0. (6.8)

Уравнения (6.7), (6.8) можно записать в форме, более удоб­ной для преобразований, представив векторные произведения в виде (так как ил и сю известны)

=^хРо» ^10 *Фо = АА)» (6*9)

Где

Что приводит к следующим уравнениям:

^ + Лй,+?0 + Уп+У#/,8(г-О==0; (6.10)

Тт

^ + А, И' + Л0д0-г^+V] &'/•’ 8 (г - .,) = 0. (6.11)

Для трубопровода круглого сечения Х2о = 0, поэтому матрица

10 —х3о 0 1 Лх — кзо ^ “*ю.

|0 *и 0 I

При малых деформациях уравнения (6.3) —(6.5) принимают следующий вид:

“Ь ^хмо“I“ о О? (6.12)

Ц =ЛДч0; (6.13)

^+ЛА-4«„=0. (6.14)

Дй

При статически определимых _задачах для определения внут­ренних силовых факторов ()о и Мо достаточно уравнений (6.10) и (6.11). Определив Д? о нз уравнения (6.11), последовательно находим вектор Лио из уравнения (6.13), вектор уо из уравнения (6.14) и вектор »о из уравнения (6.12). Для статически неопре­делимых задач для определения (?о и Л/о необходимо решить систему уравнений (6.10) — (6.14).

Рассмотренный выше частный случай уравнений равновесия трубопровода является самым простым для решения (особенно при статически определимых задачах), если принятое допуще­ние о малом изменении ио и ёю имеет место. Поэтому требуется проверить правильность сделанного предположения о малости деформаций стержня и о малом их влиянии па внутренние си­ловые факторы.

Только для абсолютно жесткого стержня можно считать, что деформации стержня равны нулю. Внутренние силовые факто­ры, соответствующие этому предельному случаю, обозначим $00 и Л7оо. Для любого реального стержня при нагружении де­формации отличны от нуля:

;=ч0 + Дч0; «„/-О; »0/-0, (6.15)

Где но — вектор, характеризующий геометрию абсолютно жест­кою стержня; Ахо, мо, — малые векторы, характеризующие из­менение геометрии осевой линии стержня, вызванное деформа­циями стержня, При малом изменении формы осевой линии стержня можно считать, что внутренние и внешние силовые факторы изменяются мало, т. е. можно принять

М0= ДЛ4; (?о=^оо“Ь

?і=0о“ЬД0! 1Ао=1Аоо-Ь ДН'о*

<6-16)

Ею=ет~~^ 4-АР*1

Подставив (6.15) и (6.16) в уравнения (5.31) — (5.35), полу­чим (сохраняя малые величины первого порядка при уо = 0)

%+*,хй»+й, Ч V т (<*-*,)= о; (6.17)

Де

Щ* + *„ X Мт- -7т XЯш+ й, + У Щ'Ь (С -.,)« 0; (6.18)

Де

АС?1“1-Ах0Х Фио^Ь?! + ЬР^Ъ(г — е,) — 0; (6.19)

—^- + у-°Х А/'И1-} Лх0х Мо()-]-Ае10хР0 |-Де10Х ДфоН“^1оХ Дф1-|-

+ А!*1+2! А^{у)В(е-*еу) = 0.

В уравнениях (6.19), (6 20) приращения с индексом едини­ца (ДЛ/ь А<?() обозначают первое приближение для внутрсн - ких силовых факторов (аналогичные обозначения введены и для векторов и|, и Ах.)). Для пулевого приближения [уравнения

(6.10) — (6.14)] имеем Д(>о = АЛ7о=0, а иоФО и Ау. оФО и Оо=И=0. Уравнения (6.19) и (6.20) дают возможность определить и ДЛ/ь которыми пренебрегли при полученииуравнений _(6.7) и (6.8). В уравнениях (6 19) и (6.20) Д^ь Дщ, ДЛ и А2ГС, счита­ются известными. Векгор хо находится из системы уравнений первого приближения (6.10) (6.14). Для статически определи*

Уых задач для определения <?1 и ДД/1 достаточно уравнений (6.19) и (6.20), так как ветчтир

SHAPE \* MERGEFORMAT

((5.21)

Зависит от малых углов ф и ф [матрица (3.16)], которые опре­деляются из уравнений нулевого приближения (6.10) —(6.14). Для статически неопределимых задач уравнений (6.19) и (6.20) недостаточно, поэтому получим уравнения, аналогичные уравне­ниям (6.12) — (6.14) для первого приближения. В уравнении

(6.13) нулевого приближения слагаемые М и ЛДю не учиты­вались, поэтому для первого приближения

/М1 = ЛДу.[.

Аналогично каждый из векторов и и О можно представить в виде

(6.23)

И для 61! И И1 получить

Ахп1-{-А0>— 0;

Йг 1 11 1

В результате получаем систему уравнений первого прибли­жения (0.19) ^ (6.20)_, (6.22), (6.24) и (6.25) (с неизвестными Д@1, ДЛ7ь Й1, тЭ'1 и Ди|). Проделав аналогичные выкладки, мож­но получить систему уравнений второго приближения и т. д.

Правильность предположения о малости деформаций стерж­ня можно проверить, сравнив нулевое и первое приближения, например, сравнив максимальные значения компонент векторов Л/о, фо, по, Оо, Дхо с соответствующими компонентами векторов АЛ71, Л^ь й, 1&1, Лч1, задавшись необходимой точностью реше­ния а, т. е.

(Д^,о)ш:«= а №п)таХ; « ((/,«1«

И т. д. Если первое приближение удовлетворяет неравенствам (АМ„и*< а(Ж(0и; №п)та*<аШты то можно считать, что предположение о малости деформаций стержня и малом их влиянии и а внутренние силовые факторы правильно. В противном случае надо решить уравнение второго приближения.

§ 7. Уравнения равновесия стержня в проекциях на координатные оси

Уравнения равновесия в проекциях на связанные оси. В боль­шинстве практических задач исследование равновесия стержней более удобно проводить, используя уравнения в проекциях на связанные оси^Кроме того, в связанных осях компоненты С}го и М, о векторов (?о и М0 имеют четкий физический СМЫСЛ (£2ю — осевая сила; ($20 и (Ззо — перерезывающие силы, Мщ — крутя­щий момент; ЛГ2о, Л'/зо — изгибающие моменты). В проекциях на связанные оси из уравнений (6.1) — (6.3) получаем (опуская знак тильды в обозначении локальной производной)

TOC o "1-5" h z ^+С33о*!-«2о*з+¥,0+9,0+V, Р|'>8(^-^')=0; (7.1)

■^+<?1о*8“Озо*1 + У20+?20+У] (*-*,)=0; (7.2)

~|~'-1-(320у1 — С?10*2-ЬУзо4' Рз*Ь (е —е,)=0; (7.3)

'~Ь30*2~М-2ихэ~Ь ^+5 —е,)=0; (7.4)

Ш + МкЧ - МпЪ - СЗво+И-яэ + V] (« “е.)=0; (7.5)

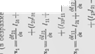
{■ СЙЧ-УІЗЧ + ^оЧ' «1™») *2 +

Де

+ VзоН”*7зоН- ^2° 8 (® —е/)—и-

Уравнения (7.4) — (7.0) остаются без изменения, так как (?2 и Оз от Р0 н шо не зависят.

Частный случай уравнения равновесия. Получим уравнения равновесия стержня, когда деформацией стержня можио пре­небречь, из системы (7.1) — (7.91):

Ддв° х20^8°~~хзо^2о + ?ю + —в/) —0;

-^+*»«ю-*Л + ?20+ ^Я^З(в-е,.) = 0; (7.17)

~ в'°- + — *2о0ю + ?зо + Аі0в (є — з,) = 0;

—Ь*20^40~*30-«2о 1 ~ЬЗК[^8— г/[ — 0;

^ + *»0^10 - «Л - С>зо+1*20+ V тУ'Ъ (г-В;)=0; (7.18)

——1- х„,Л/20 — Хд/Иц, + Сл)+і‘8о+^^ ®з;,8 (в — е/) = 0;

—^------- Ь к20й3 — *30н2 — 0;

І л

—Г Хзомі ~ хіоиз “ т—0; —^3— + *мй2"" Ъ)1к +Ф=0;

—^ *зо'^ + х2оТ ~~ д*і — 0;

+*# — ад—д*2=0;

-ІІ----------------- *ао0 + *юФ — Д*з=0;

А? до-—цД5С^5 А420-/^22^ ^*2» ^^20:гГі^31

Soo -

Ез = + Изсез. (7.22)

Где по — угол подъема винтовой линии. Ограничимся случаем, когда деформа­циями трубопровода, вызванными потоком жидкости, можно пренебречь, т. е воспользуемся уравнениями (7.17) — (7.21), которые для рассматриваемого примера принимают вид

ДО0 _

-^+ЛА) = 0; (7.23)

-f Л%М0 = — AqQq,

[Сй[5] — (ро + ei + Qfffh +

Система уравнений (7.23), (7.24) является линейной с постоянными коэф­фициентами.

Структура системы уравнений (7.23), (7.24) позволяет последовательное интегрирование сначала уравнения (7.23), а затем (7.24) (Аналогичная зада­ча для цилиндрической пружины рассмотрена в работе [46]).

Получим решение однородного уравнения (7.24), полагая

<?о=А>.

После преобразований получаем характеристическое уравнение X3 + X (*»0 + - х|0) = О,

I которого следует, что

H = 0; X2t3 = ± ib (6 =

В. имеем частные решения

Q01 — Q02 = Аг cos We; Q03 = A3 sin

Решение уравнения (7.23) в общей форме имеет вид ~Qo = K(*)Ci,

I дс K(e) •—фундаментальная матрица решений однородного уравнения:

*.(') =

Lcos2 ад cos Ые. + sin2 ao cos ao sin We sin uq cos uq (1 — cos We)

— los ao sin Ыe cos We sm au sin We

Sill ao cos a0 (1 — cos bh) — sin a0 sm ble sin2 a0 cos We + cos» a0

(7.32)

Получаем следующие выражения для компонент вектора З0 (в связанной системе координат) :

Qi0 = сп (cos2 ao cos We + sin2 a0) + C12 cos un sin bh + C13 sin aoX

X cos ao (I — cos We); (7.33)

Q20 — — cos «0 sm bh + C2 cos We 4* C13 Sin °o sin bh',) (7.31)

Q30 = C11 sin a0 cos «0 (I — c°s We) — C12 sin a0 sin bh +

+ c13 (sin2 a0 cos We + cos2 a0). (7.35)

Следует иметь в виду, что силы Q20 и Q30 равны перерезывающим силам (Л. п,п и Q3oH) в сечении стержня, в то время как для получения осевой силы в пержне Qio(1) надо к полученному выражению для <2ю добавить слагаемое

Р0 + n-twl, Т. е. = Ою + Р0 +

Определив Qc. находим Ж0 из уравнения (7.24):

М0 = К 00 С2 + I' К (« — К) А2к (Л) dh-Cx. (7.36)

|де К(е—h)—матрица, получаемая из фундаментальной матрицы заменой е

II.| (е—h). __

Выражение для Мо можно представить как

Д/0 = K(OC2+Яi(e)Ci;

ЩА2К Wdh j (7.37)

Или в скалярной форме:

Л/ю — (cos2 ao cos We + sm2 a0) сц - f cos a0 sin ЪНсц + sin ao cos a0X X(I — cos bh) с23 +1 sin 2uq (1 — cos bh) — e sin ao cos2 «о sin We] Сц - t - + [ — sin ao sm bh + e sin a0 cos a<j cos We) сц + [cos 2u0 (1 — cos We) +

+ e sin2 cr0 cos a0 sm We] c13; (7.38)

M20 = — cos «0 S|Ii Wec2i + cos bhC22 - f - sin ao sin bhc-ц 4- [sin ao sm We —

— e cos ao Sin a0 cos We] cn 4 [ — e sin a0 sm We] c12 + [cos a0 sin We +

+ с sin2 ao cos We] C13; (7.39 )

Ж30 = sin a0 cos ao (I — cos bh) C21 — sin ao sin bUcn -f - [sin2 ao cos bh -f - f - cos2 ao] C23 + [cos 2ur) (1 — cos bh) + e sin5* ao cos ao Sin We] cu -- + [ — cos a0 sin We — e sin2 a0 cos bh] c12 + [ — sm 2a0 (1 — cos We) —

— e sin3 a0 sin We] c13, (7.40)

49

Рассмотрим возможные случаи закрепления концов трубопровода, которые позволяют определить произвольные постоянные сц. При шарнирном закрепле­нии концов трубопровода должны выполняться условия М(0)=М(1)=0. В этом случае из (7.37) получаем уравнения для определения векторов С, и С2:

/ (0) С2 =■ 0; (7.41)

К (I) С-2 +В1 (1)С1=: 0. (7.42)

Ил уравнеии! (7 41) и (7 42) следует, что С, —С2= 0.

Для шарнирно закрепленной винтовой трубки получаем следующие значе­ния компонент векторов Мо и @о:

Мю = О; ОЦ* = '> = О; О! Р = Ро + л.™?, (7.43)

Т. е. печальное напряженное состояние трубки имеет только осевую растягива­ющую силу @[0(1)-

Рассмотрим случай, когда при ь=0 трубка жестко закреплена, а при е=1 свобочная. В этом случае имеем следующие краевые условия при е=1:

5^ = 00 + ^0 + «^)?! 0; (7.44)

Л1(1) = Д (1)С2 ЬВ,(1)С,=0. (7.15)

Из уравнения (7.31)

К (1) С, + (Р0 + п^1) ~ё = 0. (7.46)

Из уравнения (7.46) находим вектор С,:

Сг=- /<~1 (1) (Р0 + п<тI) в,. (7.47)

Определив Си из уравнения (7.45) определяем вектор С2:

С2^К-1(1)А(1)С,=. к-нпв1тк~ц11)(р0+п1и>1)71. (7.48)

Для консольного змеевика поток жидкости приводит к более _ сложному начальному напряженному состоянию (все компоненты векторов (?о и Л10 не равны нулю).

Рассмотренные случаи закрепления трубки приводят к статически опреде­лимым задачам. При жестком закреплении концов трубки краевые условия связаны с линейными и угловыми перемещениями торцов, поэтому при реше­нии необходимо учитывать уравнения (7 19) и (7.20):

Оъ, - -

—(7.50)

Жп = ЛАг.. (7.51)

Уравнения (7.49) —(7 51) надо рассматривать совместно с уравнениями (7 23)—(7 24), т. е. как систему

+ДА) = 0; (7.52)

-+ЛхМ0+Аі<?о = 0;

- +Лк& — Л-іАГо = 0; ~+А~й— А& = 0.

Со

М0

І получить векторное уравнение вида

З? + Кх = о,

• К^Це)'.— матрица (12X12). __

Для определения вектора С имеем 12 краевых условии, наприг 1-ткой заделки торцов: }) «(0)=‘&(0) =0, 2) к(1)=Ф(1)=0.

В случае жесткого закрепления при е=0 и шарнирного при е—

В = 0, "м (0) = Ь (0) — 0;

Е — 1,й(1)^о, 7и„(1) = о.

Решение системы (7.52)—(7.55) можно упростить, воспользовав1 иными выражениями для @0 и М0 [(7.31), (7.36)]

Решение уравнения (7.54) имеет вид

» = К(«)Са+.|'К(' — Л)А-1 [К(А)С2+В, (А)С1]<г*

» = КС3+В2С2+В, С1.

И = /<С4 + | к (С — А) А; [ЛГ (Л) С,} + В2 (А) С2 + В6 (Л) С!] йк (7.62]

(е) С4 + В^З + В&2 + В3си (7.63)

Полученные выражения для ■& и и дают возможность определить дефор­мации змеевика для любых краевых условий с учетом влияния потока жидко­сти. Гак, например, для консольного змеевика (статическиопределимая зада­ча) ранее были определены и Л/0 и соответствующие им С и Сг- Произволь­ные постоянные Сз и С^ находим из условий 8=0, н='0,=0, что приводит к следующим уравнениям:

С3 = —В2 (0) С2 - Вг (О) Сц (7.64)

С4 =- — (0) С3 — В4 (0) С2 — В5 (0) С,. (7.65)

Определив Сз и С4, получаем точное решение задачи о начальном напря­женно-деформированном состоянии винтовой трубки, заполненной движущей­ся жидкостью.

Рассмотрим алгоритм решения задачи прн действии сосредоточенной силы (см рис 5.6). В этом случае уравнение (7.52) имеет вид (считая, что дефор­мации змеевика от Р малы)

+ЛД] = Р'»(е-е,.). (7.66)

Решение уравнения (7 66) с учетом правой части можно представить в

5о = к ООС, + [ /( (е — А) 5 (е — ек) ~Рйк (7.67)

<?0 = К (г) С, + К (е — е,.:) Н (е — ЕК) Р, (7.68)

Где Н (е—ек) —функция Хевисайда.

Определив ^о, находим

Мо - К (е) С2 + | К (£ — Л) [К (К) С, + /с (Л —ек) Н (к — ек) Р] с! к, (7.69) А); Л<ек

//(*-Ч>-!,. 4^ч - (7.70)

Выражения для Мц можно с учетом (7.70) представить в виде Гг(: ^ К (с)С2-1- К(с - к) К (II) С, г!Н + [ /<(« — /!) К (II — ек)рап. (7.71)

Для консольной трубки выражения (7.68) и (7.71) позволяют сразу опре­делить произвольные постоянные С и Сг и определить начальное напряженное состояние трубки с учетом сосредоточенной силы Р. Для других закреплений концов трубопровода определение напряженно-деформированного состояния при действии сосредоточенных сил также особых затруднений не вызывает.

Уравнения равновесия в проекциях на неподвижные оси. Из

(">.13) получаем уравнения в проекциях на неподвижные оси.

-^-+Ух.+9».о+ ] 0; (7.72)

-^-+Ъ,+?Ло+ V М->е(в-в,)=0, (7.73)

?х,0+ У Р$Ч*-е,)=0. (7.74)

Ое <йв^

Если необходимо получить уравнения, содержащие слагае­мые, зависящие от параметров потока жидкости в явном виде (что бывает удобным в ряде случаев при численном счете), то ( тагаемые, содержащие следует заменить на

Д<3х; <Юх, д_

Следует обратить внимание, что форма записи внешних сил и РЮ),входящих в уравнения (7.72) — (7.74), подразуме­вает, что эти силы относятся к силам, сохраняющим свое на­правление при деформациях стержня (как принято говорить к мертвым» силам) и постоянным по модулю. Только в этом < тучае проекции сил остаются при деформациях стержня неиз­менными. Это же замечание относится и к уравнениям (7.81) — (7.83), где имеются проекции внешних моментов. Возможен случай, когда внешние силы имеют неизменные компоненты ие - швисимо от деформаций стержня в связанной системе коорди­нат («следящие» силы). В этом случае надо <?^0 и р<г) выра - нть через и РгВозможны и другие варианты сил в зависи­мости от конкретных условий работы трубопроводов.

В ^прикладных задачах внешние силы (компоненты векторов 7о и Р,-) часто известны только или в связанной системе или в неподвижной. Так, например, распределенные аэродинамические силы да, действующие на трубопровод (или шланг), находящий­ся в потоке воздуха или жидкости, легче получить в связанной системе координат, т. е. известны qi (а не ), поэтому надо иметь соотношения, связывающие компоненты векторов в раз­ных базисах.

Получим выражения, связывающие дх } с Так как

А векторы базиса {єіо} связаны с векторами і^ соотношениям! «К0=У! *Ч*Р (К=1, 2, 3),

Исключая последовательно еко и ег-, получим

Ї=2[ 2 2 (*■*'■**

Из (7.77) следует

(Р-1,2,3).

Ж.

Считается, что элементы /гкр матрицы /С известны, т. е. извеі сию положение трубопровода до нагружения в прямоугольной системе координат. Уравнения в проекциях на неподвижные оси получили йз уравнения (5.24). Предварительно определим про­екции векторного произведения (ё|Х(?о) в неподвижных осях. Так как

ЄіХС20 =

: («і)., (і*)*, (ё3).г,

Ух, Ох,

То, воспользовавшись (7.76) и (7.77), получим

6 У. о,)=о,.-£ а,.) /,+(|! о,- £ о,.) 1,+

(7.80)

Окончательно уравнения в проекциях на неподвижные оси имеют вид

*£«(—/>-0: (7.81)

П^+^’Ох -^0х,+1>х,+^ »І<І,8(е-Є/)=0; (7.82)

-^Ч-^Ох.-^Ох. Ч ^,+ У <>Ме-е;)=0. (7.83)
1.1 к как проекции Л4Х. связаны с проекциями Мк соотноше-

• < |1Ш

<7-84)

. п-.иения (5.16) принимают вид

22,вЛ/.Л/,(=Л„К—.) (к = 1, 2, 3). (7.85)

Л равнения (7.11) — (7.13), связывающие хк с углами #, ср и 1р, но гея без изменения. Уравнение перемещений (5.21) в проск - ч па неподвижные оси даег следующие уравнения:

-——— —Л* — (/ 112^21 ~Ь =0; (7.86)

Дв

Ди%.

——(^п^120; (7.87)

—— (/ц^11 -}- 12^2а ~Ь ^г^зз)—0. (7.88)

Равнения (7.86) — ('7.88) можно представить и в несколько

И форме (через КООрДИПаТЫ ТОЧеК ОССВОЙ ЛИНИИ СТерЖНЯ Х{

11 ):

^-Л.-Ёт-------------- ^-=0. (7.89)

<?Е ~ де дв к

11з сопоставления (7.86) — (7.88) и (7.89) следует

~аГ“(7-9°)

- ■ V [уку1 есть косинусы углов между единичным вектором

И неподвижными осями Х{. Такая форма записи уравнений пе-

1 1-щений позволяет установить углы поворота естественного ч» м ранника осей при деформировании трубопровода относи - | п. по осей, определяемых базисом {е, о}. Правда, это можно | 'мгь и определив абсолютные углы поворота векторов бази- ■ {<,} относительно векторов базиса {?.,}. Но такой вариант

I пкчшя становится неудобным, если рассматриваются малые ■ '-смещения осевой линии трубопровода, когда 1ц линейно за - »и от относительных углов поворота векторов базиса {ё3}. Г» ' [угае, когда деформациями стержня можно пренебречь (и равнениях равновесия), в уравнениях (7.81) — (7.83) следует ' |М‘,ИПГЬ X. иа Хщ (ХгО —известные функции).