Механика трубопроводов и шлангов

Элементы линейной алгебры н дифференциальной геометрии

Преобразования базисных векторов. При выводе общих не­линейных уравнений равновесия и движения гибкого стержня необходимо знать методы преобразоваиня базисных векторов и их связь с геометрическими характеристиками осевой линии - стержня. Приведем основные соотношения, характеризующие положение осевой линии и сечения стержня в пространстве.

Система любых я линейно независимых векторов ёг (£=1, 2, ..., п) образуют базис {ёг} «-мерного пространства. Любой вектор а можьо разложить (единственным образом) по базис­ным векторам, т. е. представить в виде

(3.1)

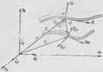
Где аг — скалярные величины. В дальнейшем, если это дополни­тельно не оговорено, под базисом {ёг} подразумевается ортого­нальный базис, определяющий ортогональную систему коорди­нат, как прямолинейную, так н криволинейную. В криволиней­ных системах координат базисные векторы при переходе в дру­гую точку пространства меняют свое направление. На рис. 3.1 показано два положения подвижных координатных осей (базиса {ёг}), связанных с осевой лннней стержня, начало которых в •системе координат х{ определяются векторами г и го. Вектор к (рис. 3.1) характеризует перемещение произвольной точки осе­вой линии стержня.

Если {в-,} (/=1, 2, 3) —некоторый базис в трехмерном про­странстве, связанный с осевой линией стержня на расстоянии £ от начала отсчета и {е-4о} — некоторый другой базис в этом же пространстве (рис. 3.1), то каждый из векторов базиса {?*•} можно разложить по векторам исходного базиса {его}:

Є1 — І IIе 10 12^20 “Ь

Є2 — 121^10 -)- ^22е2Э Н~ 12-3^30 Ї

^3 = ^31^10 ^32^23 “I“ ^2^30»

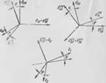Где и} — проекции базисных векторов ё* на направления, опре­деляемые векторами ё}с Элементы /,л образуют матрицу Ь (мат­рицу перехода от базиса ещ к базнсу ёг)

£=1М=

Для матрицы перехода от базиса {£,} к базису {*•;} введем обозначения К, тогда

А--II

Углы О, ф и яр, от которых зависят элементы /г,-;, не соответствуют углам при переходе от базиса {ё«3} к базнсу {е}}. Соответствую­щую матрицу, характеризующую состояние равновесия стержня,, обозначим К0 .

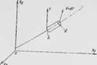
Определение элементов матрицы перехода. Найдем матри­цу перехода при произвольном смещении и повороте тройки ба­зисных векторов. Так как при поступательном смещении коор­динатных осей базисные вектора совпадают с исходными, то можно рассмотреть только преобразования базисных векторов, связанные с их поворотом (рис. 3.2). Произвольный поворот координатных осей можно представить как три независимых по­ворота. Матрицу перехода Ь получим рассмотрев поворот ис­ходных координатных осей относительно оси, совпадающей с направлением вектора ёю, на положительный угол О:

—е10;

12= сов 0 • е2о + БШ & • езо; 1з= — втд-его+созО-езо.

О • cos О sin S

О ; — sin cos ь

Элементы матрицы Л* так же, как и элементы любой матри­цы поворота координатных осей можно рассматривать как на­правляющие косинусы между векторами базисов {ё*} и {*/}- Второй поворот на положительный угол <р осуществляем отно­сительно оси, совпадающей с направлением вектора гз', полу­чаем

I=cos <р • i'i -- sin е>-/2; /2= — sin 9 • i'i -- cos <р - h h=h -

Соответствующая матрица перехода

Последний поворот координатных осей производим относи­тельно оси, совпадающей по направленню І2//=Є2_ на положи­тельный угол г]?. После чего базисные вектора і," совпадают с векторами ёг'. Соответствующая матрица перехода

Cos 0 ! — sin ф|1

0 1 О

Sin 4* О : COS^ II

Компоненты произвольного вектора а при каждом из поворо­тов (при переходе к базисам {г/}> {*/'} и {ё*}) преобразуются следующим образом:

А'—Ыа а"=Lval;

А'"=Ца".

Поэтому а"=Ь^Ь^{)а. Матрица перехода от базиса {ёг-о} к ба­зису {ёг'} равна произведению матриц £ф, и £$, т. е.

Или

Возможны и другие углы поворота трехгранника осей (в другой последовательности) так, например, для самолетных углов [35} матрица

SHAPE \* MERGEFORMAT

Соб ср соб ф — ; бш <р сое ф-|- [

- БШ & БШ Ср Б1П ф 1 4" БШ & СОБ Ср БШ ф

-

СОБ & БШ Ср

СОБСрБШф-]- : -|-Б1П& БШ СрСОБф ■

БШ ср БШ ф —

- БШ & СОБ ср СОБ ф ■

Для матриц»! Ь (любой) справедливы следующие соотношения:

£-х=/Л Ш=Е% (3.14)

Где № — транспонированная матрица, 1г1— обратная матрица. В силу условий (3.14) элементы матрицы Ь удовлетворяют со­отношениям

П. /_*ч (О 1фк)

При малых углах матрица Ь (3.13) принимает вид

(3.16)

Производные базисных векторов. Рассмотрим производные

Единичных векторов ё{ по координате 5 (рис. 3.1). Так как про­изводная от вектора по скалярному аргументу есть вектор, то представим его в виде разложения по базисным векторам {ё*}:

Да

Где к,-,— элементы некоторой матрицы ||>с»,||.

Матрица 1Ы*3|| имеет всего три независимые элемента хг

TOC o "1-5" h z

О —*3 *2

*3 0 — *1

Хо *, О

Элементы матрицы ||од[| характеризуют геометрию осевой линии стержня, с которой связан трехгранник осей.

Аналогичные выражения можно получить и для производных векторов базиса {ёг0} (рис. 3.1)

= 0- (3.19)

Вместо матрицы ||од|] можно перейти к вектору к (или ко) и вы­ражения для производных (3.17), (3.19) записать в виде

7--=*ХЄг=£к/Ікд,

' “ х0 X = елр»хро^«0»

Где

(3.22)

X = У. уе х -{- Х2(?2 -|- кзез-

При преобразованиях полезным является представление про­изводных единичных векторов в виде

Е2 е3

*2 *3

^2» й3|

'Формула (3.20) дает возможность получить выражения для аб­солютной производной произвольного вектора а, записанного

Через проекции в связанной системе координат | а, е

|кЧ да,- -

-

І ЖЧ Де і д’а , - —

Єі-- у а.—- =---------------- кХа,

1 ^ дБ *

Где д/дє — локальная производная.

В развернутой форме записи из 3.20 (или 3.23) получаем:

При выводе соотношения (3.24) никаких ограничений на на­правление векторов Є2 и ёз не накладывалось (они ортогональ­ны вектору ё|, направленному по касательной к осевой линии стержня). Возможны два случая ликвидации неопределенности направления векторов ёг и ёз - Если рассматривается шланг, ко­торый не обладает изгибной и крутильной жесткостью (абсо­лютно гибкий стержень), то целесообразно вектор ё2 направить по главной нормали к осевой линии.

Ориентированные оси, связанные с осевой линией, называют - ся естественными осями. В этом случае выражения упрощаются (так как Х2=0) и принимают следующий вид (формулы Френе* Серре [78]):

Де

Дь

(3.26)

(3.27/

Компоненты вектора Дарбу (£2) имеют следующий геометрический смысл: и3— кривизна осевой линии, — круче­

Ние осевой липни. Если рассматривается гибкий стержень, то векторы С2 и ёз целесообразно направить по главным осям сече­ния. В этом случае К2Ф0 [78] и при преобразованиях использу­ются соотношения (3.25). '

Так как главные оси сечения стержня (в общем случае) не совпадают с естественными осями, то х2 и у.3 есть проекции ра­диуса вектора кривизны осевой линии на главные оси сечения. Более подробно об этом говорится в § 5.

Соотношения, устанавливающие связь между и? и углами <р, 45, О. Воспользуемся соотношениями

(3.28)

Дифференцируя єі (328), и глеем

(3-Ю)

— де о

Исключая из (3 29)еои ——, получим

(3.30)

Дважды встречающиеся индексы можно заменять на любые

Другие (новые). Например, в первом слагаемом в левой части можно v заменить на л, в результате получим

(^/1я + /|Лр.^.^.=ЧЛ-Я (3.32)

Из выражения (3.32) получаем

Ч,,.,=(^+.^Л)/., (3.33)

В развернутом виде из соотношения (3.33) получаем следующие выражения для х* [78]:

*1 = д21 hx Н----- ^32 4" “* 4з -{-(^22;33 — ^23^32) *10 4"

TOC o "1-5" h z ds ds os

4Ft/il — 121^33) *2» 4" ft 1^32 —*30> (34)

■*2 — —7^ l\ + ^12 + ^13 + ft/ 13 — ^3/12) *10 4"

Д. da ds

4" (^33^11 — ^Al^bi) *20 H - ft 1^12 Ай^п) *30» (3.35)

*3 = '^U ^21 - J - ^12 ^22H “ ^23 4" ft 2^23 — Л/22) *104"

5 OS OS

4 {? 13^21 — ^11^23) *20 4" (^11^22 — ^12^2l) *30* (3.36)

Полученные соотношения (3.34) — (3.36) позволяют опреде­лить хх при известных х*о (иго — характеризует осевую линию стержня в статике) и углах поворота Ф, <р и яр связанного трех - I рашшка осей. Из этих же соотношений можно найти изменения соответствующих компонент вектора х (вызванное переходами в новое состояние равновесия или движения относительно со­стояния равновесия) вычитая из обеих частей равенств соответ­ствующие начальные значения х«>- Например, приращение (не обязательно малое) щ (кручение осевой линии стержня) равно

Д*1 = — *ю=~~ 4я4" J22 ^324" 1& 4" [(W33—W32) 1] х

Ds os ds

X *10+Ыя - Ш *20 4 Ыл - tM узо - (3.37)

Подставив в (3.34)—(3.36) вместо lti их выражения через У1ЛЫ 0, ф и if, получим

Х, = ^-Ј~f X1CI^ cos ф cos f — + (#1ф Sin 8 - f

-J - COS Ф sin 9 COS b) X2J + (COS Ф sin 9 sin & — sin Ф COS ft) X30; (3.38)

27

Х2 =-^— (*ю) sin ср-{- cos <Рcos &х2о+ cos <р sin ftx30; (3.39) ds v ds j

*3=-^- COS ф - J-" —Ьх10 J sin Ф COS cp-|-(sin ф sin cp sin & —

— cosФ sin ft)x2{)-j - (cos ф cosft-{- sin ф sin <p sin $)x3o. (3.40)

В выражениях (3.38) — (3.40) углы -0, <р и яр отсчитываются от положения осей {ёт}, которое принято за начальное. Эти выра­жения можно записать в виде одного векторного соотношения,. Згдобного при преобразованиях:

*"=£,-^-+а1); («"=*,Я); (3.41)

Где

В выражение (3.41) входит локальная производная по_5 (д'/дв). Следует заметить, что вектор хо(1) не равен вектору х0, который характеризует геометрию кривой в начальном состоя­нии. Вектор имеет компоненты в базисе {ё*}, равные ком­понентам вектора х^в базисе {его}-

Найдем вектор хо, характеризующий начальное состояние кривой, считая, что по отношению к декартовой системе коорди­нат {г*} известно положение базиса {ёго} в каждой точке кривой (рис. 3.1). Углы характеризующие положение базиса (ё10) отно­сительно базиса {гг}, обозначим #о(5), <ро(я), яро(^).

Базисные векторы г* и ёго связаны между собой матрицей

Следует отметить, что единичные векторы ii от s не зависят. Дифференцируя ёго по s, получим

-^~~=eKji%jGeK0- (3.44)

Так каке/0=Ар - ie, iP=kKfleKOl'to после преобразований выраже­ния (3.44) получим

„ „___ *Р ъ

Что приводит к следующим соотношениям:

Дк, Л д? о. ,

Хг,=—р - COS фо COS ср0 Sin

(?9n

Х20=——----- —— sin

■ COS ф0 -|—•

Ds

I векторной форме записи

,s d&0 .

*0=Ki-Ј--. AT,=

COS ф0 COS <Po

— sin 90 10

Sin ф0 cos <f>0 0 cos cpj

Вектор смещения точек осевой линии стержия. Как следует из рис. 3.1, вектор смещения произвольной точки осевой линии стержня И=Г—го

И=г — r0=y ({Xj — Xj0) /•,). (3.50)

Дифференцируя и по s, получим

= £ — ^ю = (^11— 1) “Ь ^12^20 “h^13^33* (3.51)

Ds

Из уравнений (3.50), (3.51) следуют полезные для преобра - зованнй соотношения, связывающие направляющие косинусы вектора <7i с производными координат точек осевой линии стерж­ня и с элементами матриц L и /С

^=V/1Pv

§ 4. Основные положения кинематики трубопроводов и шлангов

Производные базисных векторов ё, по времени. На рис. 4.1 показано положение трехгранника, связанного с некоторой кри­вой в два разные момента времени to и t>tc. Точка осевой ли­нии трубопровода, с которой связан трехгранник, при движении относительна осевой линии своего положения не меняет (s = const).

В § 3 были получены со-

О гиошения, устанавливаю­щие связь между базисными векторами кi при изменении их положения в пространст­ве из-за смещения трехгран­ника осей вдоль осевой ли­нии. В динамике изменение положения осей вызвано двумя причинами: изменени­ем положения осей во вре­мени при движении точки осевой линии стержня, с ко­торой связаны оси (рис.

4.1) и изменением положе­ния осей при переходе в со седшою точку пространства, например, вдоль осевой ли­нии стержня в фиксирован­ный момет времени т. е. базисные векторы л,(.s, t) в динамике зависят от двух независимых переменных / и s. В первом случае измене­ние положения осей зависит от изменения скалярного аргумента t при фнксиро- Рис. 4.2 ванном значении аргумента

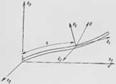S, во втором случае — от изменения скалярного аргумента s при фиксированном значении аргумента t. При движении стержня происходит непрерывное из­менение как положения его осевой линии, так и ее формы (из-за деформации стержня). Для описания движения стержня с опре­делением в каждый момент времени формы осевой линии необ­ходимо знать производные векторов связанного базиса по неза­висимым переменным t И S.

Дифференцируя векторы ёг по t можно получить следующие выражения, вывод которых аналогичен выводу соотношении (3.25)

-== —io3el--wle3;

Соотношения (4 1) можно представить и в виде (аналогично

(3.17))

TOC o "1-5" h z -^- = »хг2. ^§-=.0Хёз (4.2)

Д1 д1 дс

Или, воспользовавшись символами Леви-Чнвита,

——«кя“А= - еу«"А - <4-3>

Й К// У к 7 к

Абсолютная и локальная производные вектора по времени.

Рассмотрим вектор а{1) в подвижной системе координатных осей {с,} (рис. 4.2).

А(Л=в1(Ое,-) а2(11е2-| (4.4)

Производная вектора «(I), с учетом (1.2). равна

Да дал - . дао ~ , да* ~ , т., ~ /—ч ✓ ,7л I

------ —е л--------------- £.е2 а —I е л-а, 0« X е.) 4-а2 (ю х е2) 4-

Л л, л# * л# I/ I * V л/ I

+аЛ»х^)-=-^—Ь"Хл, (4.5)

С» а'

Где-------------- абсолютная производная;------------- локальная (относн-

О/ д*

тельная) частная производная вектора <7, характеризующая из­менение векторов « во времени относительно подвижной систе­мы координат, вектор а Ха характеризует изменение вектора а во времени, вызванное вращением координатных осей. Получим выражение, связывающее проекции векторов угловой скорости ы с углами 0, ф и і] Так как

TOC o "1-5" h z ^=//РеРо, (4.6)

Где ёро — единичные векторы базиса при і = іо, то дифференцируя

(4.6)по получим

Др ^. п — -—■

_^=_рр0=^,„,А. (4.7)

Исключая из (4.7) ёр0 получим

М. о -

Е.,> =_^/ (4.8)

к" 1 дь у

Найдем из (4.8) выражения для сог, проделав все операции сум­мирования. Окончательно получаем следующие выражения для проекций угловой скорости:

ДІ-21 , , ді'22 / . М_2Ъ_ / . //

Шг=-^(4.10) ' а/ 11 1 dt 1 1 at ' '

(„3=«lL/21+*l^/22+^/23. (4.11)

Л <5/ df 23 1

Воспользовавшись, например, выражениями для /*j (элементы матрицы (3.13)), получим

Cos ф cos ф —— sin ф; (4.12)

Dt dt

ДФ (59- .. to

102 * ~^Tsincp; (4ЛЗ)

О> =J*L - cos Ф4—— sin Ф cos ср. (4.14)

Dt т 1 dt гг 1

Соотношения (4.12) — (4.14) можно представить в векторной форме записи

(4.15)

(4.16)

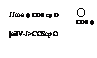Соотношения (4.12) — (4.14) можно представить и в безраз­мерной форме записи (которая используется в разделах, посвя­щенных динамике) приняв Т— ро(, (0« = (0г°р0, ГДе Т безразмер-

Ное время, си0 — безразмерная круговая частота, ро — величина, имеющая размерность частоты колебаний. Соотношения (4.12) —

(4.14) в безразмерной форме имеют вид (индекс нуль опущен):

СЛГ, и<р. ,

10* =------ COS Ф COS ср-- — Sin '

Dt dt

Йф <эд -

««2=—I-------- —- sin cp;

Dx dt

D<o, i й. ,

>3=-—— COS ф-}------ sin Ф cos e

Кинематическое уравнение, связывающее векторы со и к В ме­ханике стержней приводится следующее векторное уравнение.

(4.18)

В проекциях на связанные оси (опуская штрих в локальной про­изводной)

■=*гРз—*з^

(4.19)

Переходя к безразмерной форме записи следует принять $=/е, (/ — длина стержня); т=р0£, тц=уЛ сог=со?°Ро - Подставив в

(4.19) , ограничиваясь первым уравнением, получим

Да)1 дг.1

(4.20)

Дъ

Индекс нуль, обозначающий безразмерные величины, опущен.

Если осевая линия стержня при движении остается плоской кривой, то уравнение (4.18) обращается в тождество, так как для плоской кривой

Х1=х2=0, «)1=ш2=0 и дм31де=д*з}дх.

Для ПЛОСКОЙ кривой <йз и х3 можно выразить через угол ф (угол между касательной к осевой линии стержня и осью Х):

(4.21)

Кинематическое уравнение, связывающее векторы V и со. Рас­смотрим элемент стержня и найдем относительную скорость се­чения В по отношению к сечению А (рис. 4.3):

(4.22)

Эту же относительную скорость можно выразить и через вектор угловой скорости ю:

ЪъАв= (Й X ех) с1б. (4.23)

Приравняв (4.22) и (4.23), получим

<4-24>

Или, перейдя к локальным производным,

Х^+*х®=™хе,. (4.25)

Б проекциях па подвижные оси, связанные с трубопроводом,

— -3“ ®3К2 — ^2*3 = 0; д&

4р-+®1*з — ®Л=“а; (4.26)

Дья.

----- [- — ^*2 — ~ (,)2-

Дб’

Для получения соотношений (4.26) в безразмерной форме следует принять ^ = ^г°/ро, где £>гс — безразмерная скорость