Механика трубопроводов и шлангов

Точное численное определение частот н форм при пространственных колебаниях шланга

Рассмотрим уравнения (30.25) — (30.26) для стационарного потока идеальной жидкости, которые подстановкой вида

Их.—их1(е)т; ду*, = (32.1)

Сведем к системе обыкновенных дифференциальных уравнений вида

(32.2)

Определение частот. В ранее рассмотренном случае прямо­линейного шланга были получены собственные значения, кото­рые оказались чисто мнимыми, что говорит о том, что шланг с жестко закрепленными концами является консервативной систе­мой. Провисающий шланг также является консервативной си­стемой, поэтому можно считать л=ф. При этом среди коэффи - циептор матрицы В^'> появятся мнимые, т. е. решение (неизвест­ные функции их.^ и Д(2л-/0) слетует рассматривать как комплекс­ные функции вида

"'л="'л+г"'л' д0«л=дЙ‘л+''л^- <32-3)

В этом случае, рассмотрев действительные и мннмые части в уравнении (32.2), можно получить две системы уравнений,

Г=АГ(е, р)С (К(О, Р)=£). (32.5)

При е=0 21=^2= - =26=0, поэтому С=С2= ... =с6—0. При е=1 должно выполняться условие и{х^ = 0, что эквивалентно равенству иулю (при определенных р«) определителя

^1,7 * • *

0= : =0. (32.6)

Меняя безразмерную скорость потока жидкости Доо, нз урав­нения (32.6) находим частоты колебаний Р/ шланга в зависи* мости от скорости потока.

Определение форм колебаний шланга. Для каждого (3* полу­чаем систему уравнений для определения а:

М. ад,,+...+М. М’=0;

.......................................................................... (32.7)

“Ь - - - 4“ ^642^12* = о

Из снсгемы (32.7) определяем с71‘ ..., сц<’> в зависимости

От сцр>:

(А=1................. 6). (32.8)

Из (32.5), полагая сй*= 1, получаем собственные функции

Задачи:

=2 *$+«(=, М<£> (<4п=1), (/= 1,..., 12). (32.9)

В результате комплексные собственные векторы

(32.10)

Где 91° имеет шесть компонент фУ> с нечетными значениями / [соотношения (32.3)]; вектор имеет шесть компонент с четными значениями /. Полученные собственные векторы

Ср1г) и ч>21) могут быть использованы при приближенных методах решения (численных) более сложных задач, например при ис­следовании устойчивости колебаний шлаига с текущей жидко­стью, находящегося в потоке воздуха или жидкости.

В качестве примера рассмотрим колебания шланга относи­тельно вертикальной плоскости (30.51) н в вертикальной пло­скости (30.42) при а0=Д<7^—0. Исходная система уравнений

При колебаниях шланга относительно вертикальной плоскости [после подстановки (32.1), и, используя (32.3)] имеет вид

————«$’.=0; Л Ою

TOC o "1-5" h z аЛ2’ I (2.

—— — й<32,=0;

С1е фвд

^^+^а)+^Щ|.д(3(2) о; (32.11)

Л <3ю

_£^й_+р%« _ 25!3£ ду(1) 0

Л 010 ЧГЛ‘"

Используя метод начальных параметров, находим частоты колебаний шланга р* в зависимости от скорости потока г^о (при д:1п=0,4, #2к=0,7, см. рис. 32.1):

TOC o "1-5" h z ТРь............................... 0 0,3 0,6

Р1................................. 1,78 1,65 1,35

Р2 ................................ 3,44 3,17 2,53

Ь. . . . 5,04 4,71 4,36

На рис. 32.1 показан шланг, длина которого 103 см Размер­ная скорость жидкости

®ор=АМ (й)='(б/г)1,2= 1).

Где йУ0 — безразмерная скорость движения жидкости.

На рис. 32.2 приведен график статического натяжения <Эю, которое входит в уравнения малых колебаний.

На рис. 32.3 показаны формы колебаний для первых двух частот при Доо (для функций Д*зо(|) и АОД* )• При колебаниях шланга в вертикальной плоскости имеем систему уравнений

**£ С-*“) АО(1> I Х',0*'2а ЛО(')_0.

Йв. ф10 10 ф1С

_ Од^о) й02 + - у» АОт =п.

Д<Д£=0;

Сю

С1 —-*20

Сю

Дд^>.=0;

^0 ду(=) <1і^о)д0(9=о;

Сю Сю

Л_ и„<1) _ 2п1юпР I

Сю

++ ^<і (1 _ха) -^^0 хих'№^\^а-

(іє Сю Сю

+Р„т + Л;оХ'оДО(^) _ (, _х£) дйч =0.

Л Сю Сю

±Я£. + р, и(*)_ Л;оЛ.-оДО(.)+адві (1-Л.) Д(2ІІІ=0. а% Сю Сю

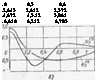В результате численного решения системы уравнений нахо­дим частоты колебаний шланга рг - в вертикальной плоскости в зависимости от гг)о: