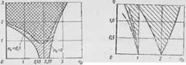Механика трубопроводов и шлангов

Методы исследования параметрических колебаний шлангов

Прежде чем перейти к непосредственному решению задач, связанных с анализом параметрических колебаний шлангов и трубопроводов, рассмотрим основные положения теории пара­метрических колебаний и методы их решения. В настоящее вре­мя этот раздел общей теории колебаний можно считать хорошо изученным. Поэтому ограничимся изложением основных особен­ностей параметрических колебаний и решением наиболее про­стых примеров, позволяющих понять физику явления и методы решения.

Решение многих задач динамики механических систем приво­дит к уравнениям с переменными вп времени коэффициентами, т. е. к уравнениям вида

У+А{£1у+СЦ)у=ВЮ/ф,

Где А(1), С(1) — матрицы с элементами, зависящими от време­ни. В простейшем случае, когда движение механической систе­мы описывается одним линейным уравнением, имеем

“о(%+%№+“.!

Характер изменения во времени параметров системы [на­пример, коэффициентов уравнения (34.2)] в зависимости от конк­ретных условий задачи может быть самым разнообразным.

Рассмотрим ряд примеров параметрических колебаний. На рис. 34.1 показана масса т, закрепленная на идеально гибком стержне, растянутом силой гДе Фм>— постоян­

Ная составляющая силы натяжения стержня; СМ£)—перемен­ная составляющая.

Уравнение малых колебаний массы /п имеет вид (без учета силы тяжести)

Рис. 34.1

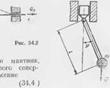На рис. 34.2 noi точка закрепления к шает периодическое (/, =(/0sinw/.

Считая угол ip малым, можно получить уравнение движения маятника

?+(у------------ ----- Sin Ш/] ¥=0. (34.5)

Уравнения типа (31.3) называются уравнениями Матье [9].

На рис. 34.3 показана классическая параметрическая систе­ма «качелн». Как известно, при определенном поведении чело­века на качелях можно раскачаться до очень больших ампли­туд, хотя никаких внешних сил к системе не приложено. Если вспомнить как раскачиваются качели, то можно нарисовать траекторию иеитра тяжести человека, стремящегося их раска­чать (рис. 34 3). Изменение положения центра тяжести человека (точки 0) приводит к изменению момента инерции системы от-

P(t)“Scce>scot

Носительно точки 0, поэтому уравнение малых колебаний чело­века на качелях имеет вид

-]- mg (/0+Д/)<р=О

ИЛИ

M0(t0--kt)2<D--2m(l0--М) Му--mg(lQ--М)<р=0, (34.6)

Где Дl(t) — периодическая функция; т — масса человека. Рас­смотренные примеры представляют собой системы с одной сте­пенью свободы. На рис. 34.4 показана механическая система (двойной маятник) с двумя степенями свободы. Воспользовав­шись уравнениями Лагранжа второго рода, получим систему двух уравнений вида

[тх - j - т2) -]- т21х1^2 + сг + с2— Сmt -- т2) glt —

— P0lj cos orfj cpj—c2f2~ 0; (34.7)

-f - Т212<&2 — ^2?i + c2 — tn2gl2 ~ Poh cos w/J <j>2=0,

Которые содержат периодически изменяющиеся коэффициенты. Параметрические колебания возникают в шлангах и трубопрово­дах (рнс. 34.5), когда скорость движения жидкости w имеет пе­риодическую составляющую Aw(t). Число примеров механиче­ских систем, в которых имеет место изменение параметров во времени, можно расширить (параметрические колебания тонко­стенных стержней, оболочек, сверл, карданных передач и т. д.), что говорит об очень широком распространении этих колебаний в различных областях техники. Среди параметрических колеба­ний имеющих место в технике, наиболее опасными являются колебания систем с периодически изменяющимися коэффици­ентами.

Основная особенность таких параметрических колебаний, делающая их в ряде случаев очень опасными при работе машин и механизмов, заключается в том, что при определенном соче­тании параметров системы возможны неустойчивые колебания.

Наиболее наглядным и убедительным примером являются пока­занные иа рис. 34.3 качели, когда из положения равновесия (точнее, при малом отклонении от положения равновесия) качели раскачиваются до очень больших амплитуд. В этом при­мере неустойчивый режим колебаний является желательным, в то время как для трубопроводов и шлангов неустойчивый режим колебаний недопустим, так как может привести к аварии.

Параметрические колебания систем с одной степенью сво­боды. Рассмотрим наиболее простые механические системы — системы с одной степенью свободы, на примере которых наибо­лее видны основные особенности математических методов реше­ния задач параметрических колебаний. В общем случае уравне­ние, описывающее параметрические колебания системы с одной степенью свободы, имеет внд

Яо И У+а1 (О У+аг (<)»=/ (<). (34.8)

В дальнейшем ограничимся случаем, когда коэффициенты уравнения (34.8) удовлетворяют условию периодичности

(34.9)

Метод Релея. Этот метод является приближенным методом. Рассмотрим однородное уравнение (34.8), коэффициенты кото­рого разложим в ряды Фурье:

=дю-1- ^ [сц бір сов/ю*) (/=0, 1, 2), (34.10)

/“0

Где

Т т

Сі} ^ аі біп (і і у = — ^ а* сов ]ь4-йі. (34.11)

О о

Решение уравнения (34.8) ищем тоже в виде ряда с перио­дическими функциями, имеющими период, в 2 раза больший (2Т), чем период (Г) коэффициентов аг, что соответствует пе­риодическому решению вблизи главного параметрического резо­нанса:

У= 51 (34.12)

При преобразованиях удобнее перейти к безразмерному вре­мени, считая

(34.13)

Где ро — характерная частота (например, частота свободных колебаний). Подставив выражения (34.10) и (34.12) в однород­
ное уравнение (34.8), после преобразований с нспользЬваииеМ тригонометрических формул имеем

Sin )Щх sin Jy' x= —(./+-§-) «з* - cos (y--------------------------- |-j n, t);

Si-n jn3x cos ~ x—-y ^sin (/+-j-j bin (y —П-J iijx'j

Cos jn^i sin -!yi-t=-~(sin (y_(—sin(y—|-j n3tj

COS У/ljT cos X = ■-i - ^cos (j + ~ j n jt + COS (y-------------------- J fi3tj.

В результате

2 Ј*’

-т+ V Ј;2)cos^-t=U. (34.15)

Выражение (34.15) должно выполняться для любого момен­та времени, что имеет место только при условиях

£<1,=£;1>(Д(, £„)= 0;

С12)--£'2)(Лк, /?„)=().

Система уравнений (34.16) есть система линейных однород­ных уравнений относительно неизвестных амплитуд Ак, Ви вида

2 («!кЛ„+ри)Вк) 0;

2 («!2к'/1„+р! к,/у=0 И=1, 3, 5,...). (34.17)

В прикладных задачах система уравнений (34.17) является конечной. (Выражения для аг-к и р*к в явном виде не приводят­ся из-за сложности.) Алгоритм получения этих коэффициентов показан при решении конкретных примеров.

Для отличного от нуля решения необходимо, чтобы опреде­литель системы (34.17) был равен нулю, т. е.

Соотношение (34.18) устанав­ливает связь между параметра­ми системы (критическими пара - 0 метрами), соответствующим и пе­риодическому решению с перио - -1 дом 2Т. Ограничившись первым приближением, получаем систе­му уравнений ~г

[“» “Чт J+Т % (т/+ Т d* (f) ■_т +

+ [^S-+^-"»f-T-(f)V1=0: f34J9)

Для. определения зависимости между параметрами уравне­ния, при которых возможно периодическое решение с периодом Т, решение уравнения (34.8) берется в виде

У=А0 + (Vini|4rB, cos^). (34.20)

/=2,4,6...

Проделав все преобразования, аналогичные предыдущему случаю, получим определитель £>2- Приравняв его нулю, получим уравнение критических параметров системы, соответствующих периодическому решению с периодом Т.

Рассмотрим колебания массы m (рис 34.1), введя силу вяз­кого сопротивления

+ + 0. (34.21)

При использовании метода Релея удобнее перейти к безраз­мерным переменным, полагая

Pot=i, !/= IV, Pq~(2Q10/ml)112, (34.22)

Где po — частота свободных колебаний (при a=AQi = 0).

После преобразований получим при AQi (/) =AQioeos (ot

•v А - плъ4- {1 - J - л 2 cos’« /г) ©=0. (34.23)

Где П4 = —^—; ff3=AQ10/Q10; п3=и>1р0.

Mp0

Приближенное решение уравнения (34.23) ищем в «виде ряда «= У, (Aj sin Jf-x+Bj cos ^-х. (34.24)

J-l, 8,5,...

Ограничимся для иллюстрации метода первым приближением

V = А sin 43+Л2 cos1. (34.25>

Подставим (34.25) в уравнение (34.23) и, сохранив только слагаемые с

ПзТЗ. Л3т

COS и sin —■ , получим систему уравнений

['-f-ffn*-''(?)”'-« И'-'"

Ч?)Ч'

Получим вначале область без учета силы сопротивления (считая п4=0). Границы областей (рис. 34.6) находятся из уравнений (34.26); так как

TO, то из (34.26) получим

(3127>

Как и следовало ожидать, неустойчивая область начинается при значении и3=2, что соответствует удвоенной частоте изменения параметра. Найдем об­ласти устойчивости с учетом силы сопротивления. Приравняв определитель системы (34-26) нулю, получим

['-т-ШИ'+тНтЛ <“»

Уравнение (34.28) устанавливает связь между критическими значениями параметров, соответствующих границам области неустойчивости. Из (34.28) находим

"’=±2iA‘(fM'-(f)I (34-29>

На рис. 34.6 штриховой линией показаны границы областей неустойчиво­сти при /24=0,5. Наличие диссипативных сил может существенно уменьшить области неустойчивых значений параметров системы. Область, соответствую­щая Лз=2, называется главной областью неустойчивости. Полученную об­ласть можно уточнить, если взять приближенное решение в виде

V = Ai sin - у т + ccs у x + A2 sin - у n3v + B2 cos-yn3x. (34.30)

В результате получаем систему однородных уравнений вида

FAl+ [' - (т n3J] Br=0:

FB1+^A1+B^O.

Приравняв определитель системы (34.31) нулю, получим

П2 f Пз 2____________ п1п3

2 2 / “ 2 2 "іпз. , п2 /”з2 п

Раскрыв определитель D, получим Я2 = /!2(Пз, П-l), ' границы главной области неустойчивости и получить (грубо) границы следую­щей области неустойчивости, соответствующей значению n2=3iz - Следующее приближение для V с шестью слагаемыми ряда позволит уточнить границы двух областей неустойчивости и получить грубые границы области неустой­чивости для n2—siz и т. д. В качестве примера рассмотрим случай, когда

HQi = AQjo cos tot -{- Д^2о (34.33)

Уравнение (34.23) примет вид

V - f n/fii - Ь (I - S - ti2 cos пгх Hb л|1) sin %t) v ~ 0. (34.34)

Опуская промежуточные преобразования, получим систему уравнений (в первом приближении)

(ад

(**41)л+[.+?^)>.-а

Уравнение для критических параметров имеет вид

«-Уі'-ШТ-ІШ'-р?-)']- «*<

Области неустойчивости (для двух случаев п4=0 и п4—0,5 при п2(1)=0,5) показаны на рис. 34.7. В отличие от предыдущего случая здесь имеется об­ласть значений п5 (1,70^ п3=^2,37), для которых при пг=0 колебания сис­темы будут неустойчивыми. Приближенное решение уравнений (34.23) и (34.34) дает возможность установить еще одну интересную особенность па­раметрических колебаний, имеющую место н в более сложных системах. В случае обычного резонанса нарастающие колебания возможны только при совпадении частот возмущающей силы с собственными частотами системы (имеется в виду консервативная система). При параметрических колебаниях

Возможны неустойчивые колебания для целого диапазона частот (при фикси­рованном пг), что делает их особенно опасными.

Чтобы определить области неустойчивости, ограниченные периодически­ми колебаниями с периодом Т, ищем решение уравнения (34 34) в виде ряда

2 (34.37)

Ограничившись первым приближением (/=2), получаем следующую сис­тему уравнений относительно Ао, Лг и Јj:

+ — ЩВ2 = 0;

(1 — /г^) Л — ЩПЛВ2 = 0; (34.38)

1ЦПгА-2 — (1 — п2,) В> + П2ЛГ) = 0.

Приравняв определитель системы (34 38) нулю, получаем уравнение

(1 - л*) (l - +,ф,= = 0. (34.39)

Область неустойчивости, соответствующая уравнению критических пара­метров (34.39) (при «4=0), показана на рис. 34.8 (область, начинающаяся в точке /г3=1). Обе области неустойчивости, показанные на рис. 34 8, получе­ны для первого приближения, поэтому при больших значениях «2 они пере­секаются, чего, конечно, быть не может, как не могут одновременно существо­вать два периодических режима с периодом 2Т н с периодом Т. Для уточне­ния границ областей неустойчивости следует взять более высокие приближе­ния. Так, например, если взять второе приближение для решения (34.37):

V = А0 + Ai sin пъъ + В2 cos п (Т А4 sin 2п3х + В4 cos ‘Jnjc, (34.40) то получаем cuci у уравнений

А) + -“ П2В2 = 0;

(1 я|) Ач — л4пА2 + ~Y~ Л4 ~ 0;

П4П3А2 + (1 — /г|) В} + щАц + —B, i = 0; (34.41)

Bi + 2л4я}Л4 -Ь (1 — 4я^) В4 0.

Приравняв оtфеделнтель систем (34.41) нулю, получаем уравнение, свя­зывающее критические значения параметров, соответствующих периодическо­му решению с периодом Т во втором приближении (при «4=0):

О-«!) [(■ -А-т)0 *3*-т(‘-«<>] +

+т[т-('-и'-т)<'-^)] '34-42>

Уточненные границы области, полученные из уравнения (34 42), показаны на рис. 34 8 штриховыми линиями Для. второго приближения пересечение гра­ниц областей происходит при больших значениях параметра я2 Приближен­ный метод Релея является очень эффективным при решении и более сложных уравнений, когда все коэффициенты уравнения (34 8) являются периодически­ми функциями [например, уравнение (34.7)], которое при &l(t) =h cos-titf после преобразований приводится к безразмерной форме [pd—x, ро= = (g//)V.]:

^1 + п + 2«2 COS n-.it + “ «2 cos 2/г,(т| <*>т — 2/г2«з С1 + «2 cos /г3т:) X

X sin n3r-f + (1 + п-2 cos л3т) у = 0, (31.43)

Где n2=lift0.

Найдем область неустойчивости, соответствующую главному параметриче­скому резонансу, считая

: преобразований получаем два уравнения, связывающие п2

Обласп. неустойчивости показана на рис 34.9 На рис 34.9, и показана область нсусч ойчввости при малых значениях «2, на рис. 34 9, б —при боль­ших значениях я2, которая интересна тем, что при больших значениях щ (при «з=2) возможны устойчивые режимы колебаний.

В зависимости от коэффициентов «г (/) уравнения (34.8), области не­устойчивости могут существенно отличаться по своей форме от областей, по­лученных для уравнения Матье

Полученные приближенным методом Релея области неустойчивости остав­ляют некоторое сомнение в точности |1 соответствия истинным областям при точном решешш исходных уравнений Поэтому рассмотрим метод точного численного определения областей неустойчивости

Метод Флоке Решение любого линейного однородного уравнения можно представить в виде

У (0 = Cl/l (0 + С2/2 (*). (31.46)

Частные решения всегда можно выбрать так, чтобы выполнялись условия: f=0. /i(0) = 1, ’/f(0)=0; f2(0)=0; Ш = 1.

Уравнение (34.8) имеет периодически изменяющиеся во времени коэффи­циенты с периодом Т, поэтому вид уравнения при добавлении к t периода Т

Не изменяется [так как ai(t+T)=ai{t)', что говорит о том, что и функции

Л(*+?") и h{t+T) являются частными решениями. Следовательно, частные решения /i(0 и /2(0 линейно связаны с решениями fi(t+T) и h(t+T), г. е.

Fi (< + Т) = «n/i (/) + ай/2 (t);

(34.47)

/2 (*+Г) = «2l/l W + аоз/2 (0-

Общее решение (34.8) при t--T имеет вид

Y(t+T) = Ci fi (t + T) + c2fi {t + T). (34.48)

Из (34.48) при t=0 получаем значение общего решения ij(t) через пери­од изменения коэффициентов. Естественно предположить, что значения 4/(0) и у(Т) связаны соотношением

У(Т) = Ю{0). (34.49)

При р— 1 решение (34 48) является периодическим. В общем случае ре­шение уравнения (34 48) может быть и непериодическим, поэтому ..ф 1. Счи­тая, что соотношение (34 49) справедливо и для произвольного момента1 вре­мени (0<*<Т), имеем

Y(t + T)=w (it), (34.5U)

Т. е. рассматривается множество решений, которые за период изменения коэф­фициентов меняются {х раз Если продолжить этот алгоритм поведения ре­шения на последующие периоды Т, то получим следующие соотношения.

Y{t-y 2Т) =w(t+T) = № (0; (34.51 )

Y(t+nT) = vny{T). (34.52)

Соотношение (34.52) позволяет сделать выводы о возможных поведениях во времени решения (предположив, что (г И.-4ВССГИ0). Если fi> 1, то решение уравнения (34.4G) при п-*-оо неустойчивое, если j. i<I, —решение устойчивое

И при р,= I — решение периодическое. Значения параметров системы, при ко­
торых |л=1, соответствуют границе области неустойчивости. Подставив в (34 50) выражения (34 46) и (34.48) с учетом (34.47), получим систему двух уравнении вида

(ап — р.) С1 + а21«2 = 0;

«12^1 + («22 — |х) С2 = 0.

Л’О решения этой системы необходимо, чтобы выполня-

I

(«11 — р) «21

[ «12 («22 — р) I

[£ — (аи + «22) Р + («11 «22 — «Г2«21) = 0. (34.55)

В силу свойств частных решений из (34.47) имеем

/г (Г) = /2 (Т) = а21 - (34.56)

Дифференцируя (34.47) по I и полагая ^=0, получим

/1 СП = «12'» /2 (У) = «22- (34.57)

Ич соотношений (34.56), (34.57) следует, что для определения элементов необходимо уравнение (34.8) численно решить 2 раза от нуля до Т. Из (34 55) получаем два значения 2, которые позволяют сделать заключение л устойчивости решения. Рассмотрим более подробно уравнение (34.55). В силу свойств корней алгебраических уравнений имеем

Р-1Р-2 = «11 «22 — <^12К21» (34.58)

НМ = /1 (Г) У г (Г) - /1 (Т) /2 (Т). (34.59)

Частные решения и Ь удовлетворяют уравнению (34.8) (при яо=1),

/1 + «1/] + Й2/1 = 0; (34.60)

/2+^1/2 +«2/2 = 0. (34.61)

Умножив уравнение (34 60) на /2, а (34.61) на /1 и вычтя получающиеся

Соотношения, получим уравнение

(/1/2—/2/1) --a(flf2 — /2/1) = 0. (34.62)

Интегрируя его, имеем

-{с, аг

/1/2-Л/1 = ое 0 . (34.63)

В силу начальных условий (при /=0) для функций /г получаем с= 1. По­этому при I = Т имеем

/I (П/2(П - /2(Г)/1 (П = е, (34.64)

1*1(12=6 . (34.65)

Рассмотрим возможные численные значения правой части (34 65). При положительном постоянном «1 (что эквивалентно наличию силы сопротивле­ния) правая часть всегда меньше единицы: < 1.

Это возможно в двух случаях: при |Х1<1, р2<1, что соответствует устой­чивым колебаниям (затухающим) п при ^ - I, (.!_.< 1, что соответствует не­устойчивому режиму колебаний. Если «1 — отрицательное постоянное число (физически это эквивалентно «отрицательному» трению), то

{Л]р,2 > 1- (34.66)

В случае (34 66) или оба корня, или одни из корней больше единицы, т. е. колебания всегда неустойчивые. Если а (/)—периодическая функция:

(34.67)

То выражение (34.65) принимает вид

= 1 • (34. 68)

Соотношение (34.68) выполняется при следующих значениях корней: при Р1>1, Ц2<1, ЧТО СООТВСТС! ВуеТ неустойчивому режиму; при р.] = р,2=±1, что соответствует периодическому (или почти периодическому решению) режиму колебаний, И При р1,2=и±ф1 если ||1| — «2+Р2=1, что соответствует устой­чивому режиму колебаний, так как в этом случае (Л, можно представить в

М^=Иг±,? = е±1¥. (34.69)

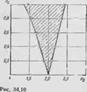
В качестве примера рассмотрим уравнение (34.23) прн /г4=0. Задаваясь рядом значений п2, определяем п3, при которых корни уравнения (34.55) ста­новятся комплексными, что соответствует границе области неустойчивости.

В результате численного решения на ЭВМ уравнения (34.23), при «4=0 получены точки границы области неустойчивости, показанные на рис 34.10 кре­стиками Сплошной линией показаны границы, полученные по методу Релея [соотношения (34.27)]. Как следует из рис 34 10, метод Релея (даже в пер­вом приближении) прн небольших значениях /?2 прнвочит к результатам, оче. пь мало отличающимся от точного метода Флокс.

Вынужденные параметрические колебания. Как следует из общей теории уравнений с периодическими коэффициентами, уст ановившийся режим колебаний возможен только в случае, если правая часть уравнений явля­ется периодической функцией с пе­риодом, равным периоду изменения коэффициентов уравнений. Точный метод определения амплитуд уста­новившихся колебаний дает воз­можность получить решение только численно, что не всегда бывает удобно в расчетной практике. По­этому представляют большой инте­рес приближенные методы опреде­ления амплитуд установившихся параметрических колебаний, кото­рые позволяют для несложных за­
дач получить конечные соотношения в аналитической форме. Установившиеся вынужденные колебания возможны только в случае, когда правая часть уравнения (34.8) есть периодическая функция с периодом, равным периоду изменения коэффициентов уравнения. Правую часть можно разложить в ряд Фурье:

/Р)=/о+ 5 (/1 у йпш1+/уСов№), (34.70)

/V) sin X-rffi f2i=-y ^ /М cos У“<-Л.

О о

Решение уравнения (34.8) ищем в виде

У=А0-1- ^ И/ sm № ~Ь вicos• (34.71)

/=1,2

Подставив в уравнение (34.8) выражения для коэффициен­тов (34.10), правую часть соотношения (34.70) и решение

(34.71) , после преобразований получим систему неоднородных уравнений

^ (УуЧ+/$)в/)=лг‘11;

/-оЙ. з 2)

V Гу^+Л^Я,) = *?’.

/=0,1,2,3

Которая позволяет определить амплитуды гармоник Aj и В3 и тем самым получить решение уравнения (34.71). Более подроб­но метод определения А3 и В3 показан при решении конкретных примеров. Рассмотрим частный случай приближенного решения

(34.71) для /=0; 1; 2, ограничившись первыми слагаемыми ря­дов для йг и f(t), т. е. уравнением (перейдя к безразмерному

Времени)

(<%>+% sin nsx--d0i cos nzт) Ј/+(«io+cii sin n&--d ц cos n3t) у + +(fl2o+ci2sin fi3t--di2 cos л3т) */=/0-f - fu sin ft3T-f /21 cos n3T.

(34.73)

Полагая

T/=Ло+Л| sin /г3т -|- cos «Зт --A2 sin 2n3x + B2 cos n2t, (34.74)

После подстановки (34.74) в (34.73) и соответствующих преоб­разований получим систему уравнений для определения Aj и В3.

Параметрические колебания систем с конечным числом сте­пеней свободы. Рассмотрим приближенные методы решения си­стем уравнений с периодическими коэффициентами.

Метод Релея. Систему линейных уравнений, описывающих колебания системы с п степенями свободы с учетом сил вязкого трения можно представить в виде векторного уравнения

Y + AW(t)y + A<V(t)y=ef(t). (34.75)

В общем случае элементы матриц Аи А(2) могут быть про­извольными функциями времени. В дальнейшем ограничимся случаем, когда элементы матриц AW и Л(2) есть периодические функции с одним и тем же периодом. Если компоненты вектора / отличны от нуля, то имеют место вынужденные колебания си­стемы с п степенями свободы. Для исследования устойчивости параметрических колебаний полагаем /(/) =0.

Ограничимся случаем, когда элементы матриц A^(t) и Л(2)(0 можно представить в виде

А$=ajj} - j - } cos wt - f-dff sin «tf, (34.76)

’ cosrf+d}? bin <•>/.

Такой вид принимают коэффициенты матриц, если их разло­жить в ряд Фурье и ограничиться только первыми слагаемыми

Ряда. В этом случае матрицы AW и А& можно представить в

Виде

Л<ч tt) = А[1) + Д',1’ cos Ы + Ah11 sin Ы;

1 (34.77)

A<2> (/J — A^ + A1,1’ cos mf + Ap sin w/.

Переходя к безразмерному времени (полагая pit=r, где pi — низшая частота системы), получим (сохраняя старые обоз­начения для матриц)

JT+(/l! i1)+Jli1)cosn3t+^1,sin л3г)у+(Лр + л12> cos n$t - j -

-j-Ap sin n3x) y=0. (34.78)

Периодическое решение уравнения (34.78) с периодом 2Т ищем в виде

У— ^jj|j (^г s*n cos • (34.79)

Размерность векторов а3 и bj соответствует размерности век­тора у.

Подставив (34.79) в уравнение (34.78), получим

Cos Л(21} sin п3х) laj cos —-1—

— bj-^-sm [(.Ao2> + .Ai2> cosщх + аР sinn3x) X

X^sin^-t+^cos-|S-tjj = 0. (34.80)

Объединяя слагаемые с одинаковыми тригонометрическими функциями

Cos х и sin т, получим

2 2 3

^ (ск sin t + rf„ cos-^-^O, (34.81)

Что приводит к системе уравнений

^=0, ^К^0(к=1, 3, 5...). (34.82)

Векторы ск и йк линейно зависят от векторов щ и Ъ}, т. е. си­стема (34 82) есть однородная система уравнений относительно векторов a, j и Ъ}. Определитель этой системы, приравненный ну­лю, дает возможность получить уравнение, связывающее крити­ческие значения параметров системы, соответствующих грани­цам областей неустойчивости. Уравнения (34.82) позволяют ■определить главную область параметрического резонанса, а также области, соответствующие периодическим решениям с пе­риодами, равными —— (/=3, 5, 7,...). Для системы уравнений

(34.82) область неустойчивости в общем случае является об­ластью многомерной в отличие от ранее рассмотренных систем с одной степенью свободы.

- Для получения периодических решений с периодом Т, реше­ние уравнения (34.78) ищем в виде

У=ас-- [а} sin х--Ъ; cos—(34.83)

{в соответствии с частным случаем — системы с одной степенью свободы).

Получим решение уравнения (34.78) (с периодом 2Т) в пер­вом приближении:

Y=alsm~-x--b1cos~~x. (34.84)

После преобразований получаем систему векторных урав­нений

J^2)- Е + РІР -± Л1,2’] щ + [ — А(о'> -|— А[1> - f +

+ ^-^2)]fcI = 0; (34.85)

—L^<2>]п = О,

2 J 1

ИЛИ

АЛ=0, (34.861

Где

А=

ЛР—І-лР - і-^2,-лі1,-^-лР^- лї^+лГ’-^+ілІ2' лГ-^-г-^'Ч+Ілі2’!

Й1=Н. N

Критические параметры системы удовлетворяют уравнению

Det 0г=0. (34.87)

Уравнение (34.87) позволяет установить область главного параметрического резонанса. Для получения области неустой­чивости, соответствующей периодическому решению с периодом Т, ищем решение в виде

У=а0--а2 sin n3t b2 cos п3х. (34.88)

Подставив (34.88) в уравнение (34.78), после преобразований получим систему уравнений

Ж2)а0+-у (М"Ч+АІ2)) в2+±-(А{2) - Ail)n3) Ъ2=0;

А РЧ - f - А^п3а2 - J - ИР — Яз£ ) Ь2=0;

ЛЇЧ+(Ло2> — /zlf) а2—Ло1)/г802=0,

Или

АД2=0, (34.90'

Приравняв определитель матрицы 02 нулю, получаем урав­нение, связывающее критические значения параметров системы, соответствующие областям неустойчивости с периодом Т.

Вынужденные параметрические колебания. Уравнения вы­нужденных малых колебаний системы с п степенями свободы можно представить в виде векторного уравнения с правой частью.{уравнение (34 75)]

У+ #■"%+(34.91)

Ограничимся случаем, когда матрицы Аможно предста­вить в виде (34.77) (переходя к безразмерному времени), а век­тор / (f) в виде

/ (t)=/0-}- /, sin ги$-- /2 cos nax. (34.92)

Уравнение (34.91) в этом случае принимает вид

Cos «st-|-Ля4 sin n. iX) у--А!>2) +А[2) cos«3r-}-

-j - А?2) sin п-Лт)у—В/0-}-В/, sin пгх--Bf%cosя3т. (34.93)

Прнближенние решение уравнения (34.93) ищем в виде

У=щ-- V [a. j sin jtijX--bj cosy /кг]. (34.94)

У—1,2,3...

Подставив (34.94) в уравнение (34.93) и ограничившись пер­вым приближением, получаем систему уравнений для определе­ния йо, «1 И Ъ1

4*4+--у (А^п3 + АР) ах + j - (Ар - A^nJ *,=В/0; (34.95)

А(22)а0 + {А(о2> - Г&Е) а, - А^'пф^ -= Bf{, лГ’ао + А^пТа, - (Л&2’ - пЕ) =ВU § 35. Параметрические колебания шлангов

В предыдущих параграфах данной главы были рассмотрены примеры параметрических колебаний систем с одной и несколь­кими степенями свободы, которые используются и при исследо­вании параметрических колебаний систем с распределенными параметрами, к которым относятся шланги и трубопроводы. Предварительно уравнения малых колебаний в частных произ­водных одним из приближенных методов сводятся к уравнени­ям в обыкновенных производных (воспользовавшись, например, принципом возможных перемещений), что уже неоднократно делалось при приближенных методах определения собственных значений.

Как уже указывалось, в реальных условиях при перекачке жидкости ио шлангам добиться стационарности потока практи­чески невозможно, т. е. давление в шланге и скорость течения жидкости имеют переменные составляющие, что было учтено при выводе общих уравнений движения шланга (29.6) и уравнений малых колебаний шланга. Особенно опасны переменные по вре­мени составляющие потока жидкости, когда они имеют перио­дический характер, т. е. при

Рх[х-{-Т, в)- Р1(х, е). (35.1)

Для идеальной несжимаемой жидкости [частный случай урав­нения (28 8) при /ц=0] имеем

Дгиг дРл 0 п.

Пл —— =-------------- . (35.2)

1 Дх дч к ’

Интегрируя (35.2) но е, получаем

Р=-п1 ~^-сЫ^с=-П1у^-ь+с - (35.3)

Если давление ка входе Рю известно, то произвольная функ­ция времени

С=Рад (0, х). (35.4)

Если на «выходе» давление постоянно, то Р (1, т) — 0, и

Окончательно получаем

Дио дх

В § 30 были получены уравнения малых колебаний шланга. Для вязкой несжимаемой жидкости имеем (считая, что формула Дарси-Вейсбаха справедлива и при наличии пульсирующей со­ставляющей скорости, когда гУ1<вУо, т. е. /ц,

Дш ___ дРх

Дх де

При тех же условиях на входе и выходе получаем выражения для Р1 (е, т):

Рг (гт] =п1 (1 - е)--а12тит1( 1 — е). (35.7)

Обоснование возможности линеаризации силы вязкого со­противления Дарси-Вейсбаха при неустановившемся течении вязкой жидкости дано в работе (63]. Так как для несжимаемой жидкости скорость от координаты е не зависит, то ее [при
известном Рю(0, можно наптп из уравнений (35.5) — (35.7) при е—О соответственно для идеальной и вязкой жидкости:

П1-^ = рю. (35.8)

•в»1®0'®1 = р*>- (35.91

Из уравнения (35.8) получаем

J1 Pyjlx с. (35.10)

Если за начало отсчета времени взять момент времени, когда *01 = 0, то произвольная постоянная равна нулю и скорость

=~ ^ Р,„ (х) dx. (35.11)

Для вязкой жидкости [уравнение (35.9) после интегрирова­ния при Wi (0) =0] получаем

™i = j P‘m(*i)e'“''-">ilx (к= 2а^° у (35.12)

Ограничимся частным случаем, когда

Ли -=Рт cos пгх> (35.13)

Где /2з=и/ро — безразмерная частота (со — размерная частота пульсации давления), что приводит к следующим функциям для скорости W\

Для идеальной жидкости [из (35.11)]

Pm п.

Щ=—— sin й3т; (35.14)

Для вязкой жидкости [установившийся режим исходя из

(35.12)]

TOi=^00K. ccs"3T + Р1тп3_ - у (35.15)

(Щ + К'2) щпл Щ (п + к2)

Для идеальной жидкости окончательно получаем следующие значения Р и Ш1:

Р (£, т)=(1 — е) Р100 cos л3т; (35.16)

Щ (?) = - Рш sin /t3t=mu sin пгх, (35.17)

«1«3

Которые войдут в коэффициенты уравнений (30.30).

Если в качестве основного параметра используется Шю, то входящее в (35.16)—(35.17) Р100 следует выразить через Юю:

Рщо— пхп3щ0.

Исследовать параметрические колебания шлангов возможно, только воспользовавшись приближенными методами решения дифференциальных уравнений в частных производных. Один из возможных методов изложен в § 26. С учетом переменных со­ставляющих потока, система (30.20) — (30.21) в векторной фор­ме записи, аналогична системе (26.5) — (26.6), может быть представлена в виде (включив в уравнения силы вязкого сопро-

Тивления а0

SHAPE \* MERGEFORMAT

(и, Дф) і2(77,

^ 6*2 1 дчдг

=

-^+Со ДС2= 0; .-(-ЛИ—+ а0 — Лм>-

1 <Эе2 1 0 д*

В соответствии с соотношениями (35.16) — (35.17) элементы матриц А& и — периодические функции. При исследовании только параметрических колебаний (устойчивости н установив­шихся режимов параметрических колебаний) вектор Ду следу­ет считать равным нулю, что и сделано в дальнейшем. Для

Идеальной жидкости диагональные элементы о«® матрицы Л<3> равны

Система уравнений (35.19) —(35.20) дает возможность ис­следовать динамическую устойчивость при возникающих пара­метрических колебаниях шланга, а также исследовать вынужден­ные параметрические колебания. Следует отметить, что парамет­рические колебания провисающих шлангов, вызванные пульси­рующими составляющими параметров потока, всегда являются вынужденными, так же как и криволинейных трубопроводов.

Полагая, как это было сделано в § 26,

«= У/i1?“’; aQ=V/W,

Можно получить систему уравнений относительно неизвестных функций и Ограничившись первым приближением, полу­чаем следующие два уравнения (при Дд=0):

ЛнЛ1>+*п/51)+С!!’/!'’—ъ$ ofi>/iI,+afi)/P»=о,

Лц=J bl=~j

*н = | K-'l'VV') ■f«o(T(,,-?(I))]*;

4J>= f [(¥-<1>.^Ч)-(Л<4У(1,-?<1))]Л: (35-26)

Н исключив ее из уравнения (35.24), получаем уравнение прост­ранственных параметрических вынужденных колебаний шланга (в первом приближении)

Ли^’ + бцЛ'Ч с,,/!1’ - by, (35.28)

Где