Механика трубопроводов и шлангов

Динамическая устойчивость стержней, взаимодействующих с потоком воздуха или жидкости

В § 21 были получены нелинейные уравнения движения стержней, взаимодействующих с потоком воздуха или жидкости, которые позволяют исследовать как нелинейные колебания стержней, так и линейные колебания относительно состояния равновесия. В первой главе, а также в § 18 указывалось, что стержень, нагруженный аэродинамическими силами, зависящи­ми от движения стержня, является неконсерватнвной системой (автоколебательной). Для неконсервативных систем при опре­деленных сочетаниях параметров системы внешнего потока воз­духа или жидкости возможны неустойчивые режимы малых ко­лебаний. Явление быстрого роста амплитуд колебаний часто наблюдается в линиях электропередач (см. рис. 1.2), при букси­ровке тросом (см. рис 1.4), при сверлении глубоких отверстий (см рис. 1 8) и т. д. При проектировании систем, где использу­ются гибкие пли абсолютно гибкие стержни, взаимодействую­щие с потоком воздуха или жидкости, необходимо знать крити­ческие параметры (например, предельно допустимую скорость при буксировке и т. д.). при которых система становится днна - 160
мически неустойчивой. Определить критические параметры си­стемы можно, если есть уравнения возмущенного движения (на­пример, линейные уравнения малых колебаний). Исследованию малых колебаний неконсервативных систем (в частности, упру­гих систем, взаимодействующих с потоком) посвящено большое число журнальных статей и монографий. Привести полный спи­сок всех работ, посвященных исследованию линейных и нели­нейных неконсервативных задач, практически невозможно, по­этому в списке литературы приведены только работы, близкие по тематике к рассматриваемым в данной книге задачам, и ра­боты с изложением основных математических методов исследо­вания этих задач.

Среди статей и монографий в первую очередь следует отме­тить [8; 64; 14, 15]. Динамической устойчивости стержней в по­токе посвящены, например, статьи: [4; 27; 33; 34; 39; 41; 45].

В последующих параграфах данной главы при исследовании устойчивости стержней, использующихся в различных областях техники, будут даваться дополнительные ссылки на статьи и монографии. Ограничимся изложением методов анализа дина­мической устойчивости абсолютно гибких стержней, взаимодей­ствующих с потоком жидкости или воздуха Изложенные мето­ды могут быть перенесены и на стержни с конечной изгибной и крутильной жесткостями, что приводит к более сложным урав­нениям.

Автоколебания абсолютно гибких стержней в потоке воздуха или жидкости. В § 25 были выведены основные уравнения малых колебаний стержня в потоке, нагруженного аэродинамическими силами, учитывающими движение стержня (20.3), (20.21) и

(20.34) , которые для частного случая (абсолютно гибкого стерж­ня) имеют вид (25.14):

-^- + г:„дд, = 0; (27.1)

-F - (2™

Напомним, что вектор полной аэродинамической силы (с уче­том силы Кармана, см. § 20)

Ма=Л+ A? i + &1L + "йко.

Уравнения (27.1) — (27.2) описывают малые колебания абсо­лютно гибкого стержня (нити) относительно состояния равнове­сия нити в потоке. В зависимости от скорости потока новое со­стояние равновесия (новое по отношению к равновесному со­стоянию в покоящейся среде) может существенно отличаться от равновесного состояния в покоящейся среде, т. е. критические параметры потока существенно зависят от новой равновесной формы стержня, вызванной потоком Как правило, при исследо­вании аэродинамических задач (пластины, оболочки в потоке)

Рассматриваются малые колебания упругих систем относитель­но их естественного состояния (без учета изменения геометрии упругой конструкции, вызванной потоком). Исключение состав­ляют мягкие оболочки, которые очень сильно могут изменять свою равновесную форму под действием внешних сил. В этом заключается основная трудность при исследовании динамиче­ской устойчивости абсолютно гибких стержней в потоке, так как в уравнения малых колебаний входят функции, которые могут быть определены только в результате решения нелинейных урав­нений равновесия стержня в потоке. Методы решения (прибли­женные) нелинейных уравнений равновесия изложены в § 14.

В § 25 изложены методы определения частот колебаний стержня в потоке с учетом нового равновесного состояния, кото­рое принимает нить в потоке, но без учета дополнительных аэ­родинамических сил (вектора Ада), которые возникают при его колебаниях в потоке. Было пояснено, что малое обнуление аэро­динамических сил является искусственным, однако этот прием позволяет установить частотный спектр (при 'Аца — 0 задача яв­ляется консервативной) и формы колебаний с учетом новой рав­новесной формы и, что особенно существенно, натяжения в ней. Ниже будет показано, что в значительном интервале скоростей мнимые части (частоты) комплексных собственных значений (для неконсервативных задач с учетом дп) меняются не очень сильно, поэтому найденные частоты (при А#я=0) могут служить для оценки правильности счета. Входящая в полную аэродина­мическую силу сила Кармана, как об этом было сказано в § 19, в общем случае приводит к возникновению параметрических ко­лебаний, однако ее влияние становится существенным при боль­ших диаметрах сечения, когда частота срыва вихрей одного по­рядка с частотой (например, низкой частотой) колебаний стерж­ня. Например, прн диаметре провода й= см и скорости потока г'о=15 м/с при числе зЬ — 0,2 получаем частоту срыва вихрей, равную 300, в то время как для провисающих проводов (или шлангов) первая частота удовлетворяет неравенству (на осно­вании рассмотренного числового примера в § 25)

Если /=10 м, то из (27.3) (31 < 10, т. е. в 30 раз меньше частоты срыва вихрей. Поэтому можно считать, что опасного эффекта син­хронизации частоты срыва вихрей с собственной частотой коле­баний прн возникновении автоколебаний с частотами, как пока­зывает опыт, близкими к первым собственным частотам, не про­исходит. При такой большой частоте срыва вихрей можно счи­тать, что эффект действия сил Кармана за период колебаний (соответствующей первой частоте) равен нулю. Поэтому в урав­нении (27.2) следует считать равными нулю слагаемые, опре­
деляющие силы Кармана, и в результате получаем систему од­нородных уравнений вида

|-С„Д&=0; (27.4)

+ А(№) _^ + А(п)_!^_=0. (27.5)

(27.6)

А<"> = - (А<2>+Л<4> + Л<5>+qn Ор0 sm<p„- С0).

Для определения комплексных собственных значении по­лагаем

Й=йфх-, (Да-| /3). (27.7)

Подставив (27.7) в уравнения (27.4), (27.5), получим

-^- + C04Q,„=0, (27.8)

Q, oH А<“'(а+^)5-(а2 + 2грц + р)й0=0.

(27.9)

Систему уравнений (27.8) — (27.9) можно представить в виде —+ £< ЧГ = 0, (27.10)

5ЪГ .

ІДО« I

О с0

(а + ®А - -(п+ів У-Е ~АС'

Из уравнения (27.10) получим систему уравнений, не содер­жащую мнимую единицу. Полагая

= Дд(1)-ЬгЛ^Р,; /70 = й(1)+ /«<">; Г = + (27.12)

После преобразований получаем

«'(1,4-с0д<2(,)=п;

ДО'(1)-| Лн'<1>+аАЙ‘” - р.4й(г| - (а2 + р)й(1і + 2а? й<2> = 0; Щ'т--Аи'т + аЛЙ(2) + ВЛн(1) — (а2 + рг) й12> — гаЗн'1’ = 0; ^ ^

«,(2)+с„дд(2)=о.

Систему уравнений (27.13), исключив из первых двух урав­нений системы и'(1) и и можно представить в виде

(27.14)

|дб(1

С0

-лс0

В=ЫА — {а г + Э2) О

II [ЗЛ -2<х(ЗЕ

—ЛС0 «Л — (а2 {-|32)

Решение однородного линейного уравнения может быть пред­ставлено в виде

Г=/С(е, а, 3)С (Л'(0, а, 3)=Е). (27.16)

Где/С — фундаментальная матрица решений (12x12).

Для абсолютно гибкого стержня, концы которого закрепле­ны, имеем следующие краевые условия:

Є —О, гг0(0) = 0 или и, (О) = /г2 (0)=0;

_ _ _ (27.17)

Е=1, йп(1)=0 или /г, (1)=й2(1)=0.

Для выполнения краевых условий при є —0 необходимо считать с1=с2 -сч =с7=с8=с0=0. (27-18)

Из краевых условий при є—1 следует

*1,4^4 4~*1 5^54-*1,0^64“ *1.1<Ао4“ *1,11С11 4~кіЛ2С12—^>

*2,4^4 ~Ь *2,5С5 4“ *2,6С6 4~ &%10С 10 4“ *2,11^11 ~Г *2,12^12= 0?

*3,4С4 4" &Ъ, оС5 4“ Ьб, вС6 4“ *3,1 Ао 4“ *3,1Лі 4“ *3,12С12 — Ф *7,4^4 4“ *7,5^5 *”■ *7,6^6 4" *7,10^10 “Ь *7,11^11 “Ь *7,12^12 = 0> (27.19)

*8,4^4 4" *8,5^5 4~*8,гА 4” *8,10^10 “Ь *«.11С114“ *8 12С12 = 0»

*94С4 4~*9,^54_^>6СС-Г*ЧЛСА'І |" *4,11^11 1* *9,12^12=:0- Необходимо (численным счетом) найти такие а и р, при ко­торых выполняются условия (27.19) при с, ф07 чю эквивалент­но обращению определителя системы (27.19) в нуль, т. е

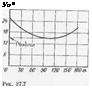
Основная трудность при определении а и |3 вызвана тем, что определитель О

(27.30) обращается в нуль без изменения знака, *1. е. касается плоскости а, |3 (рис. 27.1). Покажем, что определитель £> сохраняет знак при переходе через ну­левое значение.

Чтобы получить элемен - рис 27 I ты /г^, входящие в опреде­литель, надо исходное урав

Нение (27.14) решить 6 раз со следующими начальными значе­ниями веюора IV:

Из структуры уравнения (27.13) следует

1Г(1>(е)=-<й7,4); У(2) — >Ут= (27.21)

-- *2Р

Умножим гри последних столбца в определителе (27 23) на і и сложим с первыми тремя столбцами. В полученном после этой операции определителе умножим первые три строки на і и сло­жим их с последними тремя строками, что приводит к опреде-

-*э«+/йв,

(27.24)

В соответствии с теоремой Лапласа

В=оуо2.

Умножив элементы определителя (столбцы) 02 на —1, по­лучим комплексные числа, сопряженные соответствующим чис­лам в определителе й, т. е. определитель О равен произведению двух сопряженных комплексных чисел Полагая

(27.27)

(27.28)

Т. е. определитель О есть знакопостоянная функция. При числен­ном счете надо найти такие пары чисел а3, р;, которые обра­щают в нуль О п и £>12, т. е.

Ои (а, Р) = 0; 012(и, В)=0.

Aj. Яj

Рассмотрим конкретный числовой пример определения собственных комплекс­ных значений А* для абсолютно гибкого стержня, находящегося в потоке воз­духа, при следующих значениях безразмерных параметров: Х|К=0,9, х2к=0 при трех значениях угла а (направление потока воздуха): 0, 45 и 180°. Амп­литудные значения аэродинамических сил дпо, Ят и ды подсчитывались в со­ответствии с выражениями (19.15), (19.32), (19.37) при значениях аэродинами­ческих коэффициентов Сп=1,2; с£,=0,7; ст=0,12 (сила Кармана полагалась равной нулю).

Па рис 27.2 показаны графики изменения действительной а» и мнимой Ра частей первого собственного значения Я в зависимости от скорости ветра vn для двух чначеншй угла а (а—0 и 90°). При а=0 (рис. 27.3) действительное значение комплексного корня «1 проходит при оп=»23 м/с (точка В) через нуль и становится положительным, что соответствует наступлению динамиче­ской неустойчивости. При «=90° первая частота с ростом скорости сначала растет, а затем уменьшается до нуля (точка А), но при этом действительная часть остается отрицательной, но при va>VoA появляются два действительных корня: и, один из которых при ил>а0с (точка С) стано­

Вится положительным, т. е. наступает динамическая неустойчивость.

На рис. 27.4 приведены графики изменения действительной и мнимой час­тей первых двух собственных комплексных значений Я, (?„,=-ГХ;±1р;) и Яг в зависимости от о0 при Хи. —0.7, Л2К=0,4, «=0 (см. рис. 27.3) Критическая скорость потока (соответствующая флаттеру) в данном частном случае равна »0=»,) 1«25 м/с (точка А).

На рис. 27.5 показаны изменения а, и р! при угле а=180°, что соответст­вует противоположному направлению вектора у0, показанного на рис. 27.3. Критическая скорость потока в этом случае (точка А) существенно меньше, чем при а=0. Штриховыми линиями показано изменение а[ и [3, при учете_в

Уравнениях малых колебаний (26.5) силы вязкого сопротивления ^ и°^_)

При 00=0,1. Силы вязкого сопротивления, пропорциональные вектору скоро­сти, были введены в уравнения формально, чтобы посмотреть, как реагирует система уравнений на дополнительные внешние диссипативные силы, которые, как следует из графика рис. 27.5 (точка В), увеличивают критическую силу потока

На рис. 27.6 приведены графики изменения действительной и мнимой час­тей двух собственных комплексных значений при а=45° для провода, зак­репленного, как показано иа рис 27.3. Динамическая неустойчивость (точка А) наступает при изменении знака действительной части второго собственного значения а.

Следует напомнить, что анализ динамической устойчивости малых коле­баний абсолютно гибких стержней в потоке требует предварительного реше­ния нелинейных уравнений равновесия стержня в потоке Изложенный метод позволяет определить диапазон критических скоростей потока для конкретного варианта закрепления концов нити (провода) при изменении направления по­тока от 0 до 180° и тем самым установить минимальную критическую ско­рость (о0®) потока. На рис 27 7 дан качественный график изменения скорости По*, которое должно приниматься во внимание при проектировании линии электропередач с учетом данных о скорости ветра в рассматриваемой мест­ности