Металеві конструкції

СТІЙКІСТЬ ЕЛЕМЕНТІВ

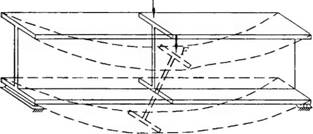
Елементи, що згинаються, можуть втратити не­сучу здатність внаслідок порушення стійкості. При досягненні критичного навантаження згин супро­воджується закручуванням стержня (рис. 3.6) у площині, перпендикулярній до площини згину. Як наслідок у поясах балки з'являються плас­тичні деформації, що швидко поширюються на весь переріз, і елемент втрачає несучу здатність.

Ейлер запропонував такий вираз для обчис­лення критичної сили:

Л • Е -1„.

G-It +

'ef

Де с — коефіцієнт, якии залежить від розміщен­ня навантаження на балці (на верхньому чи ниж­ньому поясі) і її закріплення; ief — вільна дов­жина (між закріпленнями) стисненого поясу балки; Ely — жорсткість перерізу балки при згині відносно осі, перпендикулярної до площин к1 ■ Е - Iw

Згину; GIt н---------- J----- — жорсткість при утруд-

Еї

Неному крученні; G — модуль зсуву; Iw — сек - торіальний момент інерції; It — момент інерції при крученні.

М <Ґ D

Те ж саме для косого згину:

Мх

C,.W„

Коефіцієнти сь сх, Су (а також с1лі, схм, сум для зон чистого згину) враховують вищу несучу здатність згинаного елемента у пружно-пластич­ній стадії порівняно з пружною і обчислюють їх за рекомендаціями норм. При цьому для плоского

_ - J lit' є - т

EL '

G = — (1 + v) — модуль пружності при зсуві; v — коефіцієнт Пуассона, то з (3.35) отримаємо осьової сили cN — прямокутна, а від моменту см — трикутна (рис. 3.7, в).

Аналітично результуючу епюру (рис. 3.7, в та рис. 3.8, а) можна описати як суму:

N_ М-у An L

E-Iy-G-It-

F = —

Сг,2 ef

Відповідні критичні напруження: Mcr _ Fcr - і]-І W W '

А,.,. =

Де і") — коефіцієнт, який залежить від положення Fcr на довжині балки.

2 ■ Іх

Прийнявши W = —^— у розгорнутому вигляді

(3.38)

А-

Як і для стиснених елементів, з метою спро­щення зручно подати значення критичних напру­жень через розрахунковий опір:

ОСІ. = Ц>іДуЧс. (3.39)

Згідно з нормами коефіцієнт фг, обчислюють залежно від коефіцієнтів а (значення якого на­ведено вище) та

9

Е

H fh" Фі = V, ■ н

Де ц/ — приймають за таолицями норм згідно з характером навантаження і значенням коефі­цієнта а.

Таким чином, перевірка стійкості елементів, що згинаються, має вигляд

М ^ D

А = w -

(3.40)

Де перший доданок описує епюру напружень, зу­мовлених нормальною силою, а другий — зги­нальним моментом.

Аналогічно при наявності згинальних моментів у площинах обох головних осей перерізу отри­муємо умову міцності в пружній стадії:

N М ■ у А~ + ~1 + ~ І

А ХГ> L г Г> * гі

< R„Ус,

У,71

Де Мх, Му — згинальні моменти у площинах, перпендикулярних до головних осей перерізу, відповідно X, Y; х та у — координати відносно головних осей точки перерізу, в якій сумарні на­пруження досягають найбільших значень.

Для елементів з пластичних сталей, що мають добре виявлену ділянку текучості, міцність пере­різу цим не вичерпується, оскільки значна час­тина перерізу працює при напруженнях, менших за межу текучості. Збільшення навантаження зу­мовлює текучість матеріалу спочатку лише на не­великій ділянці перерізу (рис. 3.8, б), яка посту­пово розширюється разом зі зростанням зовніш­нього навантаження (рис. 3.8, е), аж поки не охо­пить усю площу перерізу (рис. 3.8, г).

І Л' L N М=Н-с

Ті

Л*

Перевіряти стійкість елементів при згині нема потреби, якщо стиснений пояс неперервно і надій­но закріплений жорстким настилом, а також при малих відношеннях розрахункової довжини Іеі до ширини верхнього поясу Ь. Залежності для об­числення найбільших значень Іе{/Ь подані в нор­мативних документах.

Рис. 3.7. Стержні, на які діють осьова сила і згинальний момент: а — позацентрово-стиснені; б — стиснено-згинані; « — епюри нормальних напружень від нормальних сил (/); від згинальних моментів (2); результуюча епюра (,'і).