НЕУТОМИМЫЕ РЕГИСТРАТОРЫ
В самых различных отраслях науки и техники, в нашем быту встречается великое многообразие счётчиков. Они учитывают расход газа и электричества, в любой момент точно указывают число километров, которые прошёл автомобиль или мотоцикл, подсчитывают стоимость проезда пассажирам такси, считают количество деталей, движущихся на заводском конвейере.
Счётчики — основной элемент любой счётной машины.
Как по своему назначению, так и по устройству, счётчики настолько разнообразны, что на страницах этой книги невозможно рассказать даже об основных из них. Поэтому мы остановимся только на тех, которые имеют непосредственное отношение к механизированному счёту. И сразу оговоримся: в дальнейшем под понятием «счётчик» подразумевается устройство для счёта цифровых в е-
личин, автоматически производящее передачу десятков.
Как же осуществить автоматическую передачу десятков? Конструкторы отвечают на этот вопрос по-разному, но большинство решений принципиально сводится к одному: каждый разряд счётчика представляется в виде счётной шестерёнки, имеющей десять зубьев, один из которых длиннее или толще других (рис. 2).
И единица в разряде десятков. Задача автоматической передачи десятков решена.
На рисунке 2 видно, что счётная шестерня входит в зацепление не непосредственно, а через промежуточную шестерню. Без неё шестерня единиц, вращаясь по часовой стрелке, заставила бы шестерню десятков поворачиваться в обратном направлении. Благодаря же промежуточной шестерне всё получается так, как надо: шестерня единиц вра
Щается по часовой стрелке, промежуточная — против и шестерня десятков—снова по часовой стрелке.
|
/іиуїсьи} /7а л (////• Укреплён Хралі |
![]()
|
Яолесо, на моторам укреплён Храповий |
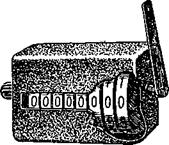
![]() По принципу, о котором мы рассказали, устроены счётчики первичного учёта или, как их ещё называют, счётчики-регистраторы. Только цифры
По принципу, о котором мы рассказали, устроены счётчики первичного учёта или, как их ещё называют, счётчики-регистраторы. Только цифры
|
Храповое Колесо |
![]() У них написаны не непосредственно на счётных шестернях, а на наглухо скреплённых с ними цифровых
У них написаны не непосредственно на счётных шестернях, а на наглухо скреплённых с ними цифровых
|
|
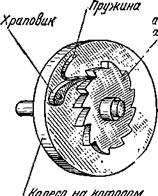
Рьс. 3. Счётчик-регистратор. Рис. 4. Храповое соединение.
Колёсах. Счётчики-регистраторы имеют довольно широкое распространение и обычно соединяются с какой-либо движущейся частью машины, каждый ход которой поворачивает рычаг счётчика, увеличивая его показания на единицу. Возможность суммирования обеспечивается применением храпового колеса и храповика для передачи движения от рычага к цифровому колесу. Этот вид соединения встречается в самых различных механизмах, от маленьких ручных часов до гигантских землеройных машин, и заслуживает некоторого внимания.
По окружности храпового колеса расположены зубья. Каждый зуб с одной стороны закруглён, а с другой — прямой.
Храповик, или, как его ещё называют, собачка, — деталь, имеющая форму клина. При вращении храпового колеса в одну сторону храповик, прижимаемый к колесу пружиной, свободно скользит по пологой поверхности зубцов. Только лёгкий трес:с сопровождает движение — это храповик перескакивает с зуба на зуб.
При вращении храпового колеса в обратную сторону картина будет совсем иной. Упираясь прямой площадкой зуба в храповик, храповое колесо увлекает за собой колесо, на котором укреплён храповик, заставляя это колесо вращаться одновременно с храповым колесом.
|
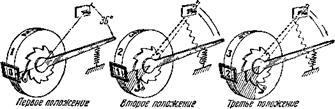
Рис. 5. Принцип работы счётчика. При каждом отклонении рычага в окошке появляется очередная цифра, увеличивая показания счётчика на единицу. |
Таким образом, нетрудно заметить, что при вращении храпового колеса в одну сторону движение его не передаётся, но зато оно обязательно передаётся при вращении в противоположную сторону.
На рисунке 5 мы видим разряд единиц счётчика. Рычаг соединён с цифровым колесом храповым соединением. Но ход рычага ограничен: он может отклоняться-только на угол в 36°, поворачивая цифровое колесо на 1110 оборота (первое положение). Поворот рычага, — ив окошке появилась цифра 1. Сделав своё дело, рычаг под действием пружины возвратился в исходное положение, а цифровое колесо осталось в покое (второе положение).
Новый поворот рычага заставит цифровое колесо продолжить вращение, и общая величина его поворота будет равна сумме двух углов в 36°. В окошке появилась цифра 2 (третье положение). При новом отклонении рычага появится цифра 3 и так далее, то-есть цифровое колесо будет суммировать единицы.
Возможность отклонения рычага только на угол в 36° не позволяет счётчику суммировать различные числа, даже однозначные. Элементарная задача 2 —3 для него уже непосильна.
Очевидно, что если дать возможность рычагу отклоняться на различные углы, цифровое колесо получит возможность поворачиваться на любой заданный угол и счётчик будет суммировать в один приём не только единицы, но и различные однозначные числа. Для суммирования мнбгознач - ных чисел надо сделать такой же привод ко всем разрядам счётчика, обеспечив управление поворотом цифровых колёс десятков, сотен, тысяч и т. д.
Задача эта впервые была решена в 1642 году, когда Блез Паскаль, впоследствии известный французский физик и математик, в то время ещё восемнадцатилетний юноша, построил счётную машину.
Хотя на этой машине и можно было складывать многозначные числа, однако передача их в счётчик должна была вестись поразрядно. Сначала устанавливались и передавались в счётчик единицы, затем десятки, сотни и т. д. В один приём воспринять всё число из-за несовершенного механизма передачи десятков счётчик не мог. Поэтому, с современной точки зрения, машина Паскаля представляет собой переходное звено от счётчика-регистратора к счётной машине.
За трёхсотлетний период существования «машинной математики», особенно за последние полвека, производство счётных машин превратилось из экспериментов одиночек-изобретателей в важную отрасль машиностроения.
Чтобы не запутаться в многообразии счётных машин, различных по конструкции и назначению, классифицируем их, постараемся ещё лучше уяснить себе термины, с которыми мы уже отчасти сталкивались, и узнаем новые, которые ещё встретятся на последующих страницах книги.
Машина должна знать, что считать, поэтому ей необходимо выдать задание — установить числа, подлежащие счёту. Это — первый этап.
Второй этап — передача установленных чисел в счётчик. Выполняя эту операцию, мы поворачиваем цифровые колёса счётчика на заданные углы, в результате чего происходит процесс счёта,
Установка чисел в машинах различных конструкций производится по-разному: поворотом установочных дисков (как в машине Паскаля), передвижением рычагов (как у арифмометра), а чаще всего нажатием клавиш установочной клавиатуры. Последний способ в настоящее время вытеснил остальные, так как оказался наиболее удобным.
|
|
|
Машины с ручной установкой чисел |
|
Математичесние машины |
|
Вычислительные Машины |
|
Тадуляционные Машины |
|
Рис. б. Классификация счётных машин. |
|
Счётные машины |
![]()
|
Машины с автоматичен кой установной чисел |
![]()
 Приспособления для передачи чисел в счётчик тоже разнообразны. Это — качающиеся рычаги, шестерни с переменным числом зубьев, ступенчатые валики, пропорциональные рычаги и так далее. Об основных из этих устройств для установки и передачи чисел в счётчик будет подробный рассказ впереди. Сейчас важно уяснить себе другое: каково бы ни было приспособление для установки чисел, но если задание устанавливает человек, то, значит, перед нами — представитель класса машин с ручной установкой чисел.
Приспособления для передачи чисел в счётчик тоже разнообразны. Это — качающиеся рычаги, шестерни с переменным числом зубьев, ступенчатые валики, пропорциональные рычаги и так далее. Об основных из этих устройств для установки и передачи чисел в счётчик будет подробный рассказ впереди. Сейчас важно уяснить себе другое: каково бы ни было приспособление для установки чисел, но если задание устанавливает человек, то, значит, перед нами — представитель класса машин с ручной установкой чисел.
Среди разнообразных машин этого класса есть предназначенные для сложения, и хотя многие из них могут также производить вычитание, — их называют суммирующими. Другие наиболее производительны при делении и умножении
(однако на них могут выполняться все четыре действия арифметики) — их называют вычислительными.
Второй большой класс составляют машины с автоматической установкой заданных чисел. Это в первую очередь счётно-записывающий автомат-табулятор, работающий в комплексе со вспомогательным оборудованием.
И, наконец, третий класс — математические маши - н ы, которые иногда называют машинами «с высшим образованием», применяемые для сложных научных и инженерных расчётов. Они уже не ограничиваются четырьмя действиями арифметики. Им доступно даже решение задач высшей математики, механики, теплотехники и других наук. О некоторых нз этих необычных машин мы будем говорить дальше.