ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ С ЧАСТОТНО­ЗАВИСИМЫМИ ЦЕПЯМИ

Обратные ИП

Обратные ИП непосредственного преобразования с ЧЗЧ строятся, как отмечено в § 1.3, по простейшей структурной схеме (см. рис. 1.1). Отдельные разновидности рассматриваемых ИП различаются между собой видом преобразуемого сигнала (синусоидального или импульс­ного) и типом применяемого ВУ.

Если в ИП синусоидального сигнала ВУ выполнено в виде ампли­тудного выпрямителя или выпрямителя — преобразователя среднего зна­чения напряжения, то его функция преобразования Z7(со) = |/С(/о)) |, где /С(/со)—комплексный коэффициент передачи ЧЗЧ [см. (1.1)]. Такие ИП целесообразно использовать для получения степенных функций пре­образования вида степенных зависимостей — на основе активных ЧЗЧ (см рис. 2.2), содержащих показанные в табл. 2.1 или 2.2 пассивные ЧЗЧ.

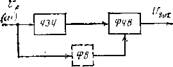
Рис. 2.9. Структурная схема об­ратных ИП с функциями преоб­разования вида вещественной или мнимой частотных характеристик ЧЗЧ

Если в качестве ВУ применяется фазочувствительный выпрямитель, на который в качестве опорного подается входной сигнал, то функция преобразования определяется вещественной Z7 (о>) = Re [/С (/<») ] или мни­мой /7(оз)=Ы[/С(/со)] частью коэффициента передачи ЧЗЧ. Входной сигнал подают на фазочувствительный выпрямитель ФЧВ (рис. 2.9) непосредственно или (если нужна функция преобразования, соответст­вующая мнимой части коэффициента передачи ЧЗЧ) через фазовра­щатель ФВ, осуществляющий сдвиг этого сигнала по фазе на я/2. Наи­более характерным примером подобных устройств являются ИП, в ко­торых для получения тригонометрических функций преобразования в качестве ЧЗЧ применяются линии задержки (см. § 2.1). В соответ­ствии с (1.1) и (2.4) выражения для этих функций преобразования записываются следующим образом [6]:

UBbix=kUf cos сот

UBMX = kUf sin (ОТ.

При выполнении ВУ в виде аналогового измерителя фазового сдви­га между входным и выходным напряжениями ЧЗЧ, т. е. преобразо­вателя разности фаз в напряжение, функция преобразования соответ­ствует фазочастотной характеристике ЧЗЧ arg[/C(/co)]. Такие ИП це­лесообразно применять для получения функций преобразования в виде обратных тригонометрических функций от переменной (0. Например, если в качестве ЧЗЧ используется пассивная интегрирующая цепь (см. табл. 2.1, схема 2), имеющая фазочастотную характеристику arg[^(/Ct))] =—arctg (о/?С, то функция преобразования имеет вид

Uв ы n~=kUо arctg /?Ссо,

где LJ0 — опорное напряжение, используемое в ВУ данного типа.

Если в ИП импульсного сигнала в качестве ВУ используется ампли­тудный выпрямитель, то функция преобразования определяется харак­теристикой ПДА F(0) в соответствии с (1.3). Если ВУ выполнено в виде преобразователя среднего значения напряжения, то вид функции преобразования существенно изменяется. Среднее значение импульсного напряжения на выходе ПДА

Ucv=(TB/T)Ue, (2.7)

где £/0 = £/т/7(0)—амплитуда выходных импульсов ПДА; Um— ампли­туда входных импульсов; Ти—длительность выходных импульсов. Так как в зависимости от пропускания однополупериодными выпрямителя­ми, входящими в состав ПДА, положительных или отрицательных импульсов

Тц = х или Ти—Т—т,

где т — длительность входных импульсов; Т — период их следования (см. § 1.1), то в соответствии с (2.7) функция преобразования имеет вид

и с р= Um (т/71) F (0) = UmBF (0) (2.8)

или

U0j> = Um[ (Т-т) /Т] F(Q)=Um(l—Q)F(Q). (2.9)

В простейших ПДА, имеющих согласно (1.2) линейную характери­стику F(Q) = —0 или Т7(0)=0, зависимости (2.8) и (2.9) идентичны:

Ucv = Um(Q—02). В более сложных ПДА (см., например, рис. 2.5) эти зависимости отличаются друг от друга. Однако можно заметить, что использование среднего значения выходного сигнала ПДА вместо амплитудного всегда повышает на единицу степень полинома в функ­ции преобразования.