Колеца Ньютона. Определения радиуса кривизны линзы
Интерференционные полосы равной толщины в тонкой пленке, т. е. темные или светлые полосы соответствующие постоянному значению толщины пленки (d), можно наблюдать в воздушной прослойке между соприкасающимися друг с другом плоской поверхностью пластинки и выпуклой сферической поверхностью линзы (см. рис.5).
При этом толщина воздушной прослойки постепенно увеличивается от центра линзы к ее краям. При нормальном (перпендикулярном поверхности) падении света полосы равной толщины имеют вид концентрических окружностей, которые получили название колец Ньютона.
Если на линзу падает пучок монохроматического света, то световые волны, отражённые от верхней и нижней границ воздушной прослойки, интерферируют между собой.
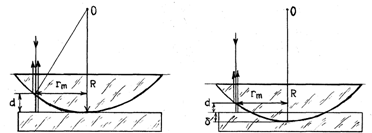Так как, в отличии от выше приведённого примера, отражение световой волны происходит в точке В от раздела среды воздух-стекло, а не стекло-воздух, как на рис.4,то λ/2 добавляется к слагаемому L1 и формула (19), в начальной её части приобретёт вид:
∆ = L1- L2 = (АВ + ВС + λ/2) - AD = 2d + λ/2
То есть, оптическая разность хода, в этом случае равна удвоенной толщине воздушного зазора (2d) ( показатель преломления воздуха n = 1).
В итоге получим: ∆ = 2d + λ/2 (23)
