REACTOR THEORY
Classical chemical engineering theory teaches us about a variety of idealized reactor types. The oldest type of chemical reactor is the batch reactor, of which the coke oven is currently the only example that is relevant to gasification (Thoenes 1994;
and Westerterp, van Swaaij, and Beernackers 1987). In the coke oven a batch of coal is indirectly heated via the side walls in a relatively flat vertical oven where devolatilization takes place. Such a batch process can also be made semicontinuous, as is the case in a coal stove for domestic use and a moving-bed gasifier (see Section 5.1), or fully continuous, as in large-scale grate-type furnaces as applied in power stations and industry. For the coal or other solid fuel the fully continuous version is a typical example of a so-called plug flow reactor.
Plug Flow Reactors. The idealized plug flow reactor (PFR) is characterized by the following properties:
• There is a continuous flow through the reactor.
• There are no radial gradients.
• There is no axial mixing, that is, there is no exchange of material or heat.
• In addition, a plug flow reactor will generally be operated in a steady state manner.
For a first-order kinetics and the generalized component A, equations 3-1 and 3-2 can be expressed as:
![]()
![]()
![]()
 |
-fcc dt - kcA
which after integration yields for the concentration after time t:
c A _ - kt
CA, 0
and for the conversion of component A:
CA, 0 ~ cА л - kt
—-------- = 1 - Є
CA, 0
These reactions also hold for a batch reactor.
Continuously Stirred Tank Reactors. The ideal continuously stirred tank reactor (CSTR) has the following characteristics:
• There is a continuous flow through the reactor.
• The contents of the reactor are ideally mixed; thus the conditions are the same at all points in the reactor. This implies that the effluent has the same composition as anywhere else in the reactor. In the CSTR the mixing time should be about two orders of magnitude lower than the average residence time to achieve this.
When we set the average residence time equal to т we derive the relation from formula 3-5 for a first-order reaction at constant density:
![]()
![]()
![]() cA,0~cA ~ кCAT
cA,0~cA ~ кCAT
and so:
CA, О кт + 1
For the conversion of component A we then get:
CA, 0 ~CA _ kT
c A, o kx+1
Equations 3-9 and 3-10 show that increasing the residence time т will increase the conversion. In some cases, this can lead to unpractically large reactors. In order to avoid this the single CSTR can be replaced by two or more CSTRs in series, which each have the same volume and residence time, but that have a combined average residence time and volume that is equal to the single stage CSTR. For N stages we then obtain:
![]()
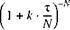 (3-11)
(3-11)
As this yields equation 3-6. An infinite number of CSTRs hence gives the
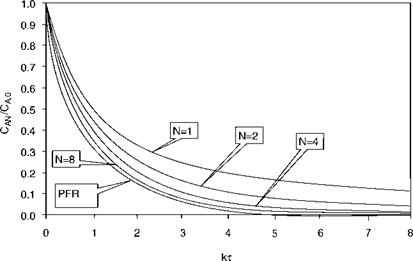
same results as a PFR with the same overall residence time. In practice a number of about four CSTRs already gives results that approximate a PFR with the same residence time, provided the conversions required are not excessive. In Figure 3-7, some comparative results are given for various values of N.
The result that a large number of CSTRs gives the same result as a PFR can easily be understood when we consider that in a single stage CSTR there is a small chance that reactants leave the reactor without having the time to react. Adding a second CSTR diminishes this chance, although the overall residence time remains the same. Adding subsequent CSTRs virtually eliminate the chance of “short circuiting” of reactants, and for the conversions given in Figure 3-7 we see that the results of the PFR can hardly be distinguished from that of eight CSTRs in series having the same overall residence time.
|
Figure 3-7. Relative Conversion as a Function of the Dimensionless Time kx |