Фотоприемные устройства и ПЗС. Обнаружение сла­бых оптических сигналов

КВАНТОВАНИЕ И ФЛУКТУАЦИЯ СИГНАЛА

Мечта каждого разработчика — свести к минимуму уровень шумов ФПУ. Пусть осуществится эта мечта и ничто не огра­ничивает возможности — ни требования аппаратуры, ни техно­логия. Тогда, выбирая площадку ФП сколь угодно малой, сни­жая фон и температуру, увеличивая сопротивление входной цепи и крутизну транзистора, теоретически можно достичь сколько угодно малых шумов (см. § 2.5). Поэтому сколь угод­но малым будет и значение порогового сигнала, если его рас­считать по формулам § 3.3—4.2. Что же тогда ограничит мини­мально обнаруживаемую оптическую мощность? Такое фунда­ментальное ограничение накладывается квантовой природой излучения: в импульсе оптического сигнала не может быть меньше одного фотона, а энергия импульса ЕсаТс соответствен­но не может быть меньше энергии этого фотона Ну. В идеаль­ном детекторе-счетчике один фотон преобразуется в один электрон, так что минимальный заряд импульса фототока сиг­нала (8ЕсАТс)пчп равен заряду электрона <?. Используя выра­жение для чувствительности (1.18), получаем

(5£,са7’с)ш1П=9'5 (^сА^[:)щ|п-^ =

-/гуА==а9/5 = 1,24<7Д=2- 10-,9Д, (4.125)

Где Яса^с [Дж]; Я[мкм].

Таким образом, в пределе минимально обнаруживаемая энергия импульса (£СА?'с)тт теоретически ограничивается не свойствами ФПУ, а корпускулярностью самого излучения и для спектрального диапазона 0,5... 14 мкм составляет (4 ... 0,15) • 10~1Я Дж. Конечно, в большинстве реальных ФПУ пороговая энергия далека от этого квантового предела: требо­вания, предъявляемые оптико-электронной системой, все-таки не позволяют неограниченно снижать площадку, фоновый по­ток, температуру; ограничены и элементная база, и выделя­емая электрическая мощность, а следовательно, ток, крутизна и электродвижущая сила шума (§ 2.5), что не дает возмож­ность беспредельно снижать уровень шума ФПУ. И все же в ФПУ с кремниевыми ЛФД, в которых в результате умножения подавляются шумы усилителя, а собственные шумы ЛФД очень малы, удается приблизиться к указанным предельным значе­ниям — регистрировать если не один, то несколько единиц — десятков квантов. Примерно к таким же значениям удается приблизиться и в специальных кремниевых ПЗС. Рассмотрим особенности регистрации столь малого числа квантов.

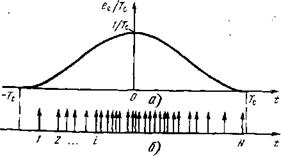
Квантование сигнала. Столь малые сигналы нельзя уже описывать, как делали раньше, детерминированной функцией Ес (0 — точно известной зависимостью оптической мощности от времени (рис. 4.20, а). Теперь надо учесть, что оптический сиг­нал состоит из отдельных фотонов:

Ес(0 =Ь[6 (*—#,) +б{(—/2) + ... +6 (*—]. (4.126)

Такой сигнал изображен на рис. 4.20,6. В силу статистиче-

Ской природы самих источников излучения и потерь на пути от излучателя до ФП оптический сигнал является случайным про­цессом: случайны моменты прихода каждого из фотонов t] . . . 1у и число фотонов з импульсе N. Как и в любом слу­чайном процессе, параметры каждого конкретного импульса (отдельной реализации) не могут быть известны заранее. Раз­работчику оптико-электронной системы могут быть известны лишь статистические характеристики сигнала. Ими становятся те же характеристики, которыми описывали детерминирован­ный сигнал: его относительная форма ес(*)> длительность Тс, энергия (мощность) [87]. Вместо энергии конкретного импульса (конкретной реализации) ЕсаТс, которую аПриори никто не знает, следует ввести среднюю энергию ЕсАТс. Удобно описывать импульсы числом квантов ЛЛ и поскольку энергия кванта к\ то

ЛГ = ЯсА7’с^; М = (4.127)

Так как под энергией ЕсаТс понимаем теперь среднее значение, то такая энергия может быть и ниже квантового пре­дела— когда среднее число квантов в импульсе меньше едини - , цы, Лг<1. Конечно, в каждой конкретной реализации содержит­ся целое число фотонов N=0, 1, 2, 3, ... Однако если преобла­дают импульсы с N=0, а импульсы с N=1 очень маловероятны — их вероятность р(1)<С1 (и еще менее вероят­ны реализации с N^2), то тогда и возникает такая ситуация со средним значением Аг<1:

Со

Л?=2^р(ЛГ)«0.р(0) + 1-/;(1)«р(1)<1. (4.128)

Л'=0

Статистический смысл приобретает также относительная форма оптического сигнала ей(1). Значение ес(1)сИ/Тс — не что иное, как вероятность любого из Лг пришедших фотонов прийти в интервале [I, t--d^]. Полная вероятность встретить этот фо­тон в любой момент I должна равняться единице. Используя выражение для эффективной длительности сигнала (2.4), полу­чаем это необходимое условие:

Ос*

^ ^ (г)^=^гс=1. (4.129)

—го

С помощью введенной функции плотности вероятности для моментов прихода фотонов ес (/)/Тс можно показать, что в пределе при большом числе фотонов N мы вновь возвращаем­ся к прежнему описанию сигнала зависимостью мощности от времени £с (/) =ЕсАес (/). Действительно, если каждый из N фотонов попадает в интервал 1,с вероятностью

Ш

Еси)Ш/Тс, то в среднем (для импульсов с числом квантов - V) в этот интервал попадет йЫ=Ме0№)(И/Тс фотонов и их энер­гия будет равна НхйМ. Тогда оптическая мощность в момент t

Ес (0 (О /7С =

=ЕсАТсео (0 (Тс=£сАес (0 • (4-130)

Замена НхМ-уЕ^аТс выполнена по (4.127). Случайные откдо - нения N от своего среднего значения N (и соответсТвенНо флуктуация Еса в (4.130)) характеризуются дисперсией ДЛ'г-^ = (;У — Щ1. Для пуассоновского процесса Д/У2 N [54], так

Что с ростом N относительные флуктуации V Д;У2/Лг=1/1'' /V становятся все слабее и слабее, реализации ЕсаТс, Ес. все МеньшЕ и меньше отличаются от своих средних значений ЕскТс, ЯсА И амплитуда Е^х в (4.130) становится опять детер­минированной величиной Еск~Ес- Это и давало право опус­кать знак усреднения во всех предыдущих параграфах, полагая

Ес А ~ ЕсА-

Обнаружение случайного сигнала. До сих пор рассматри­вали сигнал, все отличительные признаки которого были стро­го заданы, и все расчеты проводились по этим детерминирован­ным признакам (характеристикам). Теперь видно, .что сигнал случаен, так что параметры каждого падающего на ФПУ им­пульса неизвестны, известны лишь его статистические характе­ристики. Поэтому и ошибку при обнаружении (вероятность про­пуска сигнала Рпр) можно рассчитать только для статистиче­ских характеристик — средней амплитуды сигнала £с. По­скольку при больших N относительные отклонения амплитуды каждого отдельного импульса от своего среднего значения пре­небрежимо малы, то рассчитанное значение РЩ} остается спра­ведливым практически для каждой реализации импульса. Од­нако при малом значении N все чаще встречаются импульсы с малым числом квантов N (по сравнению со средним Л'), вероятность пропуска импульсов с Л^<СЛ^, естественно, возра­стает. Так флуктуация сигнала приводит к дополнительной ошибке — возрастает вероятность пропуска цели (относительно вероятности пропуска, рассчитанной для средней амплитуды).

Рассмотрим сначала «чистый» вариант — когда фотоны сигнала считаются без потерь, дополнительные шумы не вно­сятся, так что пропуск цели обусловлен только флуктуацией сигнала. Рассмотрим последовательность импульсов со средним числом фотонов М. Случайное число фотонов N в каждом от­дельном импульсе подчиняется статистике Пуассона, поэтому вероятность реализации импульса с N фотонами равна [54]

Детектор может принять решение о наличии сигнала, если на него попал хотя бы один квант. Если в реализации импуль­са вообще нет фотонов (ДГ«0), то принимается решение «сигнала нет». Поэтому вероятность пропуска сигнала будет равна вероятности реализации импульса с числом квантов ^=0. Подставляя в (4.131) значение 0, получаем

Рпр^Р (0) = ехР (-Л0 • (4.132)

Из (4.132) вытекает, что для квантового предела при аГ= 1 вероятность равна Рщ>=ехр ( — 1) =*0,37, а в обсуждавшемся случае, когда #<1, вероятность пропуска вообще стремится к единице: Рщ,= ехр (—ДО) « 1—/V» 1. Такие большие вероятно­сти ошибок в оптико-электронных системах, как правило, недо­пустимы.

Выражение (4.132) позволяет решить и обратную задачу — найти допустимое значение [А/], при котором обеспечивается требуемое значение Рдр:

[Щ = 1п (1 /Япр) = 1п {1 /0,5 ((10-з.,. ю-5»)] _

= 2,3^2 (10з.. л О9)» 7... 21. (4.133)

Численная оценка здесь проведена для типичных значений /яр (см. § 3.1). Соответственно оптическая энергия таких сигналов равна (4.127)

(Ё75«|«=ЬЛГ=2- 10-вА/[д7н

=2-10~19(7.. .21)/(05... 14)«(1.. .80)- 10-,9Дж. (4.134)

Как видим, минимально регистрируемая оптическая энергия сигнала (среднее значение) в 7 ... 20 раз выше квантового пре­дела. И лишь тогда вероятность его обнаружения удовлетво­ряет требованиям аппаратуры.

Отношение сигнала к шуму (шуму самого сигнала) равно

Л^с/ш=[ ]у] / у Ш*=I. V ] /У^Я] =у7^Г =>

; 1/(7...21)«2,6 ... 4,6. (4.135)

С точки зрения обнаружения пуассоновское распределение оказалось лучше нормального. В гипотетическом случае, если бы флуктуации сигнала подчинялись нормальному закону, ве­роятность РПР надо было бы рассчитывать из выражений, ана­логичных (3.8), (3.9):

' Р„р = |{1-Ф[(ЛГ-ЛГп<)р)/'/2Ш]]«. ,

Здесь вероятность Рпр определяется Прежде всего СИЛЬНЧЫ. экспоненциальным множителем. Полагая лУпор—1’ ДЛ'з^д^ получаем для оценки

Рпр^ехр[-(,У~ 1)2/2/У]«ехр(- ЛГ/2). (4.137)

Сравнение (4.132) и (4.137) показывает, что для обеспече­ния заданной вероятности Рпр в гипотетическом случае нор­мальных флуктуаций потребовался бы вдвое больший сигнал, чем это нужно на самом деле — при пуассоновском распределе­нии числа квантов сигнала N. Расчет по (4.135) несколько уточняет этот коэффициент, он равен 1,7... 1,8 при принятых нами значениях Рпр = 0,5 (10~3... 10~9).

Итак, мы определили минимальную (среднюю) энергию сигнала (4.133), (4.134), которая лимитируется самим же сиг­налом, его собственными флуктуациями. Пришло время по­явиться на сцене ФПУ: как оно сыграет свою роль обнаружи­теля не просто сигнала, а случайного сигнала?

Шум сигнала на выходе ФПУ с интегрирующим фильтром. Фотодетектирование случайных оптических сигналов практиче­ски не отличается от фотодетектирования детерминированных. Квантовую эффективность г| можно рассматривать как вероят­ность одного фотона генерировать один фотоэлектрон, тогда при среднем числе падающих фотонов N генерируется в сред­нем Л7С — фотоэлектронов. Это число связано с амплитудой оптического сигнала ЕсА и фототока /СЛ очевидными соотноше­ниями

-<УС — /саГ с/<7 = 5£,са7' с/д = '1дЕсь. Тс/кчд~ ■

= цЕсьТ^/^ — •пТУ’. (4.138)

Случайное число фотоэлектронов Л^, генерированных в каждом импульсе, также подчиняется статистике Пуассона [54].

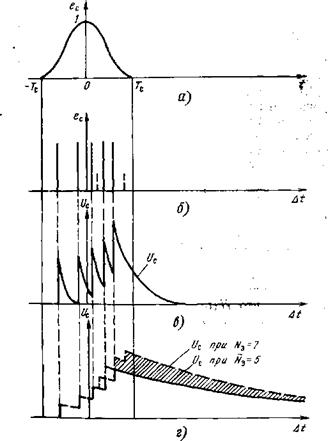
Интереснее анализ прохождения случайного сигнала через фильтр-усилитель, расчет дисперсии сигнала на его выходе. В этом разделе в качестве фильтра выбираем интегратор с не­которым временем накопления (хранения) Тн (рис. 4.21). Сек­рет здесь в том, что в таком фильтре особенно наглядно про­является физика приема сигналов, расщепленных на отдельные кванты.

Рассматриваемый фильтр интегрирует короткий импульс входного^ тока от каждого отдельного фотоэлектрона, так что выходной сигнал пропорционален заряду указанного входного импульса, в данном случае Этот сигнал хранится в течение Тн = тэ. Точное значение амплитуды выходного сигнала от одно­электронного входного импульса рассчитывается с помощью им­пульсной характеристики. Для интегратора она прямоугольная (рис. 4.21,а) и ее значение на интервале тэ равно #=КоЛ^

Рис, 4.21. К расчету сигнала и его шума на выходе ФПУ:

А — импульсная характеристика ФПУ; б~ полоса частот ФПУ уже полосы сигнала; в — полоса частот ФПУ шире полосы сигнала (полосы сопоставимы); г — произвольное соотношение лол ос

(3.138), (4.36). Выходной сигнал определяется площадью входного импульса тока д, умноженной на эту импульсную ха­рактеристику, Исх—яКаЫэ (3.137).

Несколько формальных замечаний. Поскольку отношение сигнал-шум не зависит от коэффициента передачи Ко, то для упрощения записи формул в предыдущих параграфах считали его равным единице. В дальнейшем также полагаем Ко = 1* В нашем преобразователе ток—напряжение коэффициент Ко размерен, поэтому условие Ко = 1 предполагает одновременный

Переход к безразмерным (нормированным) величинам, что и надо помнить в дальнейшем.

Итак, при /Со=1 #(*м) =^(/м) “1/^э и выходной сигнал ока­зывается равным £Ла = <7/тэ: заряд электрона как бы «размазы­вается» на интервале тэ, создавая на выходе сигнал (импульс тока) <7/тэ. Поскольку интегратор запоминает сигналы от всех фотоэлектронов Л/т, генерированных на интервале тэ, то все эти сигналы надо сложить:

1/сл = ?ЛГт/тэ. (4.139)

Вряд ли возможна более простая обработка входного сиг­нала— фильтр является обыкновенным счетчиком, считает фо­тоэлектроны 'Ух> генерированные за время тэ. Поскольку две случайные величины 11са и #с связаны детерминированным ко­эффициентом ^/тэ, то по (2,27), (2.28) их средние значения и дисперсии также связаны этим коэффициентом и его квадра­том:

РсЛ = (4.140)

Д^сА = ДЛГ? = Дг./V,. (4.14])

Тэ Тэ

Шум сигнала на выходе ФПУ нестационарен. Пока нет сиг­нала, нет, естественно, и его шума. Рассмотрим дисперсию Дис2 для момента / = когда сигнал достигает своего макси­мального значения. Расчет Д£/с2 сводится к расчету числа Лгт в указанный момент tк.

Инерционный фильтр. Если выбрать эффективную постоян­ную времени фильтра тэ достаточно большой, больше длитель­ности колоколообразного сигнала по основанию

Тэ>2Гс, (4.142)

То интегратор-счетчик успеет сосчитать (накопить) все сигналь­ные фотоэлектроны (рис. 4.21,6). Поэтому Лгг = Лгс и выражения для среднего выходного сигнала и его дисперсии (4.140), (4.141) можно записать в виде

Л^=.л7, Ис=—мс; ; - •' ' ' ; (4.143)

Тэ

■й~г-£гХс. ' (4.144)

1Э

Полученную формулу (4.144) для шумов сигнала можно «загримировать» под формулу Шотки: член #ЛГС связан с током /СА (4.138), эффективная постоянная времени — с шумовой по­лосой, 1/2тэ=/щ. б (табл. 4.1):

Д^ = ^-ЛГс=2?^^^ = 2?/сАа. А/ш. б. (4.145)

(4.146)

В (4.145) и (4.146) вошла относительная импульсная чув­ствительность (относительная амплитуда) Гс/тэ = иСА. Оказы­вается, такая замена справедлива всегда — при любой форме сигнала и импульсной характеристики, если, конечно, постоян­ная фильтра велика: Ведь в этом случае входной им­

Пульс тока можно рассматривать как дельта-воздействие с площадью /саГс, и тогда выходной сигнал воспроизводит им­пульсную характеристику Н (tM)=h{tK) — 1/тэ:

Тэ^’Т’с, Wca~ (^м)//сА— (^сдТ'с) ^(^м)//сА—^с/тэ. (4.147)

Малоинерционный фильтр. При очень малом времени Тэ«С <СТс темп генерации на этом интервале тэ можно считать по­стоянным (рис. 4.21, е). Его максимальное значение задается амплитудой сигнала IСА/<7, за время тэ на вход придет Nz = = /сТэД7 фотоэлектронов. Поэтому для выходного сигнала и его шума по (4.140), (4.141) получаем

(4.148)

(4.149)

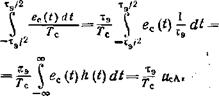Фактически (4.148) и (4.149) являются частным случаем предыдущих (4.145), (4.146)). Ведь малоинерционный фильтр Тэ<Гс не искажает сигнал, поэтому для него &СА— 1. А коль скоро (4.145), (4.146) справедливы и при очень большой, и при очень малой постоянной времени фильтра тэ, то им, по-види­мому, можно доверять при любых промежуточных значениях тэ. И это действительно так. Вероятность одного электрона прийти на интервал М равна есЦ)<И1Тс, поэтому его вероят­ность попасть на произвольный интервал тэ задается интегра­лом

(4 Л 50)

Где

ЙсА =

Эту выкладку поясняет рис. 4.21,г. Импульсная характери­стика интегратора постоянна на интервале [—тэ/2, тэ/2] и равна 1/тэ, что дает право заменить пределы интегрирования и вве­сти Л (г). Искомая вероятность обнаружить один электрон за интервал тэ пропорциональна площади под кривой £с(0 на этом интервале. Но эта же площадь задает и относительную импульсную чувствительность «са, относительную амплитуду выходного сигнала (3.138). Среднее число зарегистрированных электронов ДО, равно среднему числу пришедших на вход, умно­женному на вероятность (4.150) каждого из них попасть на интервал тэ:

^т=Л^(^исА) = -^^«са=^-ЛаКса. (4.151)

Подставляя значение Л^х в исходные выражения для сигнала и его шума (4.140), (4.141), приходим к формулам (4.146),

(4.147):

УсА = -£.Я, = -^(-£/саИса) = /сл«са. (4.152)

Т» ТЭ Я / , .

Ди? = 1^-1саИса) — 2?/сАЙсА - тД - = 2?/сАйса/ш.6. (4.153)

Тэ Ч / ^ Гэ

Полученные формулы для шума и сигнала настолько естест­венны, что, кажется> их можно было и не выводить: ведь это хорошо известные выражения дробового шума от постоян­ной засветки, только здесь в роли засветки выступает сам сиг­нал. Такая «подмена» постоянной засветки сигналом очевидна при малой постоянной времени усилителя тэ<С^с. Действитель­но, в течение столь малого времени наблюдения сигнал почти не меняется и ФПУ не способно его отличить от обычного посто­янного тока. Этому току всегда сопутствует белый шум спек­тральной плотности 2^/са (при м)> действующий в полосе усилителя /ш-б, так что можно сразу записать формулу для дисперсии выходного шума (4.153).

Справедливо и обратное рассуждение: постоянный фоно­

Вый и темновой ток /0 = /фф+/т можно, в свою очередь, считать сигналом, но только бесконечно большой длительности Тс - Любой усилитель с конечной постоянной Тэ будет малоинерци­онным для такого «сигнала», поэтому для его шумов справед­лива (4.149), причем /са = Ль «са=1. Еще раз вывели формулу дробового шума, полученную раньше в § 2.3.

В общем случае сигнал не остается постоянным на интер­вале наблюдения тэ. Но если сигнальный заряд, пришедший за это время, равномерно «размазать» по интервалу т3, то как раз и получим средний ток на этом интервале /са«са (4.152) — штриховая линия на рис. 4.21, г. Он и ответствен за шум, об­щая формула (4.153). При Тэ^$>Тс усилитель успевает зареги­

Стрировать весь заряд сигнала ЬАТс, так что при «размазыва­нии» по интервалу Тэ получаем средний ток /СА Тс/т (рис. 4,21,^)- Этот ток и входит в частную формулу для дробо­вого шума (4.145).

Отношение сигнала к его собственному шуму по (4.145), (4.146) равно

А'с/ш = ^са/УЛЛ^с2Н<7/*э) Мх/У(дутэ2)ЛГт = 1/гДГт. (4.154)

Сравнивая полученное отношение ЛГс/ш на выходе ФПУ с этим же отношением для самого оптического сигнала (4.135), легко увидеть, почему и как влияет полоса усилителя на дегра­дацию этого отношения. Оптимальным оказался усилитель с большой постоянной времени тэ^2ТС) когда регистрируются все фотоэлектроны Л^ = #с. Если этот усилитель не шумит и квантовый выход высокий, то потерь в отношении сигнал-шум практически нет и Nx = Nc? zN. Быстродействующий усилитель не успевает считать все фотоэлектроны сигнала Л^<Л/с, и чем меньше постоянная времени тэ, тем заметнее потери в отноше­нии сигнал-шум.

Так выбранный фильтр-интегратор помог наглядно предста­вить преобразование шумов сигнала. В § 3.5 было показано, что любой фильтр можно в первом приближении считать нако­пителем С некоторым эффективным Временем накопления Тэ, так что полученные результаты должны иметь общий характер. Но все-таки — как повлияет конкретная частотная (импульс­ная) характеристика на шум сигнала? Повторим расчеты, но уже в самом общем виде для произвольного фильтра-усилителя и с учетом умножения.

Шум сигнала на выходе произвольного фильтра-усилителя. Запишем выражение для реализации смеси сигнала с шумом ФПУ на выходе этого ФПУ:

£/(0 = г/ш(0+£М0. (4л55>

Учтем теперь, что случайным является не только шум ФПУ но и сам сигнал ис (0 - Поскольку договорились опреде­лять пороговые свойства относительно среднего значения сиг­нала, то выделим в приведенном выражении среднее значение сигнала £/с(0 и его случайную составляющую — шум сигнала

Д£/с(/) = £/с(0-Е( 0:

У(0 = ^ш(0+Д^с(04-£Гс(0. (4.156)

К собственному шуму ФПУ £Ли(/) добавляется некоррелиро­ванная с ним компонента — шум сигнала Д{УС(/). Так ока­зывается, что сигнал «мешает» сам себя обнаружить, и разра­ботчику ФПУ недостаточно учитывать «свои» шумы: если шум ФПУ мал, то приходится учитывать и шум сигнала.

Найдем выражение для случайного сигнала ^с(0> а затем рассчитаем необходимые величины: среднее значение

Ис(1) и дисперсию Д ис2^). Каждая фотоактивная генерирован­ная светом пара, разделяясь в момент наводит во входной цепи короткий импульс тока с зарядом дМ (в отсутствие умно - жения можно полагать М= 1). Соответственно на выходе ФПУ появляется импульс дМН((—/*), повторяющий по форме им­пульсную характеристику #(£—ti). Выходной сигнал опреде­ляется суперпозицией таких парциальных импульсов от каждой разделенной пары [87]:

... + ДМк^Н (* — (4.157)

Здесь, как и в оптическом сигнале (4,97), случайны момен­ты прихода импульса и число этих импульсов Мс. При ис­пользовании ЛФД (а именно эти ФП обычно и позволяют «вы­тащить» шум сигнала над шумом ФПУ) появляется третья случайная величина — умножение МПри расчете среднего значения £/с(0 учитываем, что случайные величины А4* и N. независимы, так что усреднение будем проводить последо­вательно и раздельно по каждой из них. Один квант вызывает на выходе сигнал ис (£) = дН^—^i) со случайным моментом прихода /*. Поскольку вероятность моментов ti задается выра­жением ес(1)/Тс, то усреднение по ti приводит к такому значе­нию среднего сигнала от одного кванта:

Ос '

Ис(() = ч 1 , (4.158)

— С©

При наличии умножения заряд каждого такого импульса увеличивается в среднем в М раз. В среднем на выходе прихо­дят Агс таких парциальных импульсов, так что для среднего сигнала получаем окончательно

ИгЩ = чйЛ Ц - <5 . (4.159)

I —со *

При £ = (4.159) дает амплитудное значение, соответствен­

Но интеграл определяет относительную амплитуду иса (4.150). Заменяя по (4.138) д№с}Тс = 1са = 8ЕсА, получаем

Со

= ЛЖисА=

— ОО

(4.160)

Получили стандартное выражение для расчета сигнала на выходе ФПУ (3.141). Найдем теперь среднеквадратичное зна­чение флуктуации сигнала Дис2. В отличие от проведенного расчета среднего значения теперь надо усреднять квадрат пар­циального импульса <?2Л^2Я2(/—и). Проведя усреднение в прежней последовательности, получим выражение, аналогичное ^4.159), только в него войдут уже не линейные, а квадратич­ные члены ц1, Мг2 = М2, Я2. Однако число Лгс остается в первой степени. Ведь все парциальные импульсы от каждого из ЛГС фотоэлектронов независимы, так что их дисперсии просто скла­дываются:

= ^ (4.161)

^—оо >

Проведя традиционную замену qNc/T<z = IzK, перепишем ^4.161) еще в одном виде:

Д(7с2=дисНи=2?/сАЛ12 -1 $ ЕАіі)НЦ(„-<,)Л,|. (4.162)

Теперь главное—разобраться с интегралом в фигурных скобках (4.161), (4.162). Как всегда, попытаемся подобрать ключ к решению задачи с помощью предельных случаев.

Инерционный фильтр. При тэ~^>ТС импульсная характеристи­ка фильтра Я (*м—*<) медленно меняется по сравнению с «бы­стрым» сигналом ес{іі), поэтому Я2(/м—^) можно считать поч­ти постоянной величиной и вынести ее за знак интеграла:

= = -^-ЛГсмЬ. (4.163)

= 2д1сКМшсь/у. (4Л64)

Здесь учтено, что Я(/м) =А(/м) = 1/тэ; 1/2тэ = /у (табл. 4.1), - Иса—Гс/тэ (4.147) и что площадь под кривой ес(/<) есть эф­фективная длительность сигнала Тс. Точно так же для сигнала (4.158) получаем

И^)=чы, мнцк)Ц - ^ (4.165)

Ч —ОО /

Возвратились к нашим старым выражениям для сигнала и •его дисперсии на выходе фильтра-усилителя (ср. (4.165) и (4.143), а также (4.163) и (4.144). Новое здесь лишь умноже­ние. Удивительного в таком совпадении формул ничего нет: любой фильтр является интегратором для короткого импульса, поскольку его реакция пропорциональна площади этого корот­кого импульса. Получается, что любой достаточно инерцион­ный фильтр считает все фотоэлектроны сигнала ЛГС, а при ум­ножении — все умноженные электроны ММС.

Интересно проследить за формой выходного сигнала в этом случае: она детерминирована, всегда повторяет импульсную характеристику, случайна лишь амплитуда, которая опреде­ляется случайным числом электронов на входе М-Л1. Нагляд­ной иллюстрацией к сказанному является рис. 4.22. На рис. 4.22, г приводятся две реализации выходного сигнала: непрерывная линия соответствует случаю, когда на вход приш­ло среднее число квантов N(1 (в примере для конкретности Агс = 5), а штриховая — это реализация с Л^с = 7. Как видим, и

Средний сигнал ис{Д/), и его шум £/с(*)_ис{1) одинаково за­висят от времени, а отношение шума к сигналу определяется этим же отношением для падающего числа фотонов N (точнее, фотоэлектронов = А последнее равно 1/]/ЛГс при М= 1. К такому же результату приводят формулы (4.164), (4.165):

С (*и) — Я У ^Ж2/<]МСМ -

^/Ж2/^с^2=^/^с - (4.166).

Ухудшение в УГ раз происходит из-за флуктуации умно­жения.

Быстродействующий усилитель. Вернемся к исходной фор­муле для шума —к интегралу в фигурных скобках (4.162) и оценим его значение для быстродействующего усилителя. При Тэ<7с функции ес(*с) И —^) меняются местами. Теперь

Почти постоянен сигнал, поэтому вынесем его за знак инте­грала:

|ве <*«) у 5Я2 (<" - ={И № {(а~*4 (4-167)’

Здесь учтено, что ес(*м) = 1. Теперь наш интеграл напоми­нает свертку (3.138), с помощью которой находится выходной сигнал. Точнее, он совпадает со сверткой, когда входной сигнал повторяет по форме импульсную характеристику, т. е. при £(/)=//(/„—*,)/ 2:

СО <»

ИсА(О = ^ е, ((,) H(t№-ti)dt,=<S)m (/„-(,) ли. (4.168>

— 00 —ос

Но ведь это случай оптимального фильтра!

В пространстве частот ситуация выглядит так: на вход уси­лителя подан сигнал, амплитудный спектр которого совпадает с относительной частотной характеристикой этого усилителя, £е(/)=ес(/)=*Ш (3.45). В этой записи также учли, что на низких частотах плотность спектра нашего сигнала

Я(<,)/2«1:

£ол-Я(<«)/2=1/2т„; Т0-=т,; £,(/=)- =27-0£сд=2тэ(1/2тэ) = 1. (4.169)

Поэтому для амплитуды выходного сигнала получаем

Оо со

<УсА (<„) = С £с (/) к (/) а/ = $ & (/) с1/. (4.170).

О о

Это очень полезный результат. Интеграл оказался равным амплитуде сигнала на выходе оптимального фильтра £/са, а она, в свою очередь, равна шумовой полосе /ш>б (последняя

28 Г

Особенность уже отмечалась в § 3.3, см. (3.51) с учетом усло­вия И Так что формула для шумов сигнала (4.162)

Принимает очень естественный для такого рода формул вид:

Д!77= 2?/саЖ2/Ш)(3. (4.171)

Форма выходного сигнала (одна из возможных реализаций) представлена на рис. 4.22, в. В отличие от предыдущего случая инерционного усилителя, теперь случайна не только амплитуда, но вся форма ис^). Она имеет гребенчатый характер: каждый «зуб» гребенки — это отклик системы на единичный входной электрон со случайным моментом прихода

Предельные выражения для дисперсии сигнала на выходе инерционного (4.164) и быстродействующего (4.171) усилите­лей подсказывают сами, как их можно обобщить на случай произвольной постоянной тэ:

2<7/са«саЛГ2/ш. б = г^/сдйсА^/У/у (4.172)

Здесь введена эффективная полоса для шумов сигнала /ш. б и, как всегда, ее отношение к эффективной полосе уси­лителя /у

^ —йо

Нетрудно заметить, что выражение для дисперсии шума сигнала (4.172) переходит в свою первозданную форму (4.162), если в него подставить коэффициент Г/ по его определению (4.163).

Итак, ФПУ сыграло свою роль — обнаружило случайный сигнал. Поставленная задача выполнена: среднее значение сиг­нала преобразуется по тому же алгоритму, что и обычный де­терминированный сигнал (4.160). В течение эффективного вре­мени наблюдения тэ сигнал создает на входе усредненный ток /са^са — этот ток и отвечает за шумы сигнала. Все своеобразие расчета свелось к определению шумовой полосы /'ш. б для дис-

# Персии случайного сигнала. В общем случае она определяется не только усилителем, но и самим сигналом — его относитель­ной формой ес (?) и соотношением его длительности Тс с эффек­тивной постоянной времени усилителя тэ. Но этот результат ин­тересен скорее теоретику, чем практику: полоса /'ш. б

Варьируется при изменении тэ/Тс в достаточно ограниченных Пределах ОТ /ш. б —Г'/у ДО /у, соответственно коэффициент ГI — от Г1 до 1 (см. (4.164), (4.171)). В книге рассматривается че­тыре примера фильтров-усилителей (табл. 4.1). Для двух из них — уже рассмотренного выше интегратора, а также усилите­ля с прямоугольной частотной характеристикой — указанные полосы вообще совпадают: //ш*б=г/ш*б~/у, Так что

Отмеченная вариация полосы /'ш-б проявляется только в /^С-фильтрах, прежде всего в однозвенном, для которого Т*,— 0.5. Можно предложить использовать при расчете диспер - сии шума (4.172) следующие аппроксимации для коэффициен­та Г/1

= + 2; (4.174)

Г;ап —ГА+^э/Т'с)2]/!! (4.175)

В (4.174) считаем коэффициент Г^п постоянным, равным среднему значению Гг (тэ). Даже при ТакоЙ примитивной

Аппроксимации ошибка в расчетЕ шума У Д£/с2 однозвенного

Фильтра не более чем в УГШ/ГХ = >^0,75/0,5 = 1,22 раз - (в 1,1 раз —у двухзвенного). Более придирчивого читателя должна удовлетворить вторая из аппроксимаций. По рис. 4.23 она отслеживает реальную вариацию шумоВой пОлосы и обес­печивает погрешность расчета шумов Д£/с2 в пределах 2 ... 5% (для рассмотренных #С>фильтров).

Общий случай: шумы сигнала и ФПУ сопоставимы. Шумо­вое число. При сигналах, близких к квантовому пределу, к общему шуму ФПУ надо добавить еще одну найденную компо­ненту— шум сигнала (4.156), (4.172). Это относится ко всем полученным в предыдущих параграфах формулам для отноше - йия Л'с/ц]. Так, (4.55) с учетом формулы для /ш (4.162) прини­мает теперь вид

= ^сайсаМ//Т Г-у/у//?вх -}-

"" + 2? (ЛаИсаЛ'/Г, + /о) + 4 Сх (2л)2Г2/у3. (4.176)

Величины сигналов и их шумов были определены числом

^Рис. 4.23. Оригинальность эффективной полосы усилителя для шумов сиг­нала состоит в ее зависимости (хотя и слабой) от длительности самого

Сигнала:

А — однозвенный фильтр! б — двухзвеняый фильтр

Фотоьктоонов Я* Шум ФПУ также удобно выраЗИТЬ

Тектрои с у —. перехода от тока

Через некоторое шумовое число Лщ. ДЛЯ у наблюде. к чис», электронов надо этот ток умножить н Р „ак по

Ния („ Эффективную постоя"и7»е®^МеегН0Ин^ 9, находим число чаем регистрируемый; заряд. Разделив его ч»

Фотоэяжтронов (4.151). отношения #с/ш на мио-

Укаожая числитель и знаменатель отно ы1- через

ЖитедТэ/4?> получаем в числителе сигнал, вы^аженн ре»

19«. а и знаменателе шум, только его дро-

Ности ьыкладки удержим сначала в шум

Бовую компоненту:

(4.177) (4.178>

(4.179)

^Дм^А - ^4Л8°*

Здесь составляющие шума сигнала и ФПУ разделены. Что­бы выРажения для шумов сигнала и ФПУ были симметричны, введем следующее определение шумового числа.

Уш «оу=лгшД^г,'. 14Л81)'

Сопоетавляя (4.180) и (4.181), видим, что при таком опре­делении

^ш^(Г,/Г,')Яо. (1182)

Т. е. по физическому смыслу шумовое ЧИСЛО Л>Гш ЭТО среднее число з^екТрОНОВ темнового (общего) тока N0, зарегистриро ванное и фПу за время Тэ> Дробовой шум этих первичных элек­тронов определяет шумы ФПУ. Коэффициент (А/А ) ВОЗНИ кает из^а пересчета шумов ФПУ, которые действуют в полос А/у» к Полосе шумов сигнала А7у* В широкополосном усили тели ли^о интеграторе этот коэффициент исчезает, так ка

Г / — А*

Если заметны и тепловые шумы ФПУ, то их можно заме нить эк^}шалентньш генератором тока /ш и соответственно эк внвален*ЙЫМи значениями Л^0 и В этом случае в (4.180)

284

Для шумов ФПУ сохраняем все компоненты шума. Остается лишь внимательно проследить за этой достаточно громоздкой выкладкой:

4к Т

: _2qhM ‘Frjy +f^- Л/, + («ц, С„2я/у)2Г2/г]

=lsIi-M2Frt (2т,/,).

+ (tsЈsЬ-)2r2(2fyx,)*f,

Введение Nx и Агш позволяет привести отношение сигнал - шум (4.160) к простому и наглядному выражению

ЛГС/Я= UjUv=NxM/VNrM’FT,' --МшМгРГ=

“^/^(Ж+ЛуТТу. (4.183)

Минимально обнаруживаемая мощность. Минимально обна­руживаемую мощность (энергию) малых сигналов нельзя рас­считать простым умножением шума на требуемое отношение Агс/ш (см. § 3.1). Есть ряд обстоятельств, усложняющих такой расчет.

Прежде всего сам шум нестационарен и зависит от наличия сигнала, поэтому априори непонятно, какое же значение шума надо брать для такого расчета — в темноте либо при сигнале. Остановимся подробнее на этом обстоятельстве.

Вспомним, что требуемое отношение сигнал-шум (см. § 3.1) выбиралось из условия обеспечения заданных ошибок обнару­жения — вероятностей ложной тревоги Ялт и пропуска цели ЯпР:

Рд, = [ 1 — Ф ({/ Mf/V2U^t/2 = [ 1 — Ф (гс„/ Г"2)1 /2, (4.184)

А, р={1 - Ф {(С/са— £/„„р)/^2г/ш1}/2=

: =[1-Ф(«„р/]/2)]/2, (4.185)

■UmfIUm^A'mp/y (4-186)

<£/сА - = (ЛГ, - ЛГМр)/1//г/'(Лг,+ ЛГи). (4.187

С/ш ~ллт -}- /2пр. (4.188)

Здесь введены парциальные отношения ппр и плт. Из (4.184) и (4.185) следует, что это аргументы интеграла вероятности Ф.(ялт/ К 2) и Ф(пПр/ V2), при которых гарантируются ошиб-

285

Ки не более заданных значений Ли и Рйр. Поскольку ложная тревога — это ложное решение о наличии сигнала, когда его нет, то в формулу (4.184) для Рлт входит шум в отсутствие сиг­нала (4.184), (4.186). Поскольку пропуск цели — это ложное

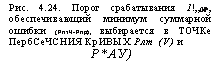Решение об отсутствии сиг­нала, когда он есть, То расчет Лгр должен прово« диться по значению шума при наличии сигнала (4.185), (4.187). Если шум сигнала пренебрежимо мал (Ж<^ш), то сумма парци­альных отношений плх и Пщ> дает обычное отноше­ние сигнал'Шум 17С, ш= - исА/иш (4.186) — (4.188). Введенное в (4.186) и (4.187) число Л;пор= ~Тэ£Люр/Я — это порог сра­батывания, при превышении которого принимается ре­шение о наличии сигнала (см. § 3.1).

Зависимости Рлт и Рир от £/ПОр (интегральные распределения выходного напряжения и без сигнала и при сигнале) представ­лены на рис. 4.24. Здесь эти распределения условно считаются пока нормальными. Раньше, когда сигнал не влиял на шум, распределения РЛт(^пор)> Рпр(£/пор) были идентичными по форме, только сдвинуты друг относительно друга на величину сигнала С/СА (см. § 3,1). Теперь из-за разной дисперсии шума эти распределения отличны и по форме. Но, как и прежде, ми­нимум суммарной ошибки Рлт-Ь^пр достигается при выборе по - рога Л/пор В точке пересечения Кривых Рдт^-Рпр (чуть-чуть пра­вее этой точки). Объяснение этому прежнее: при любом сме­

Щении порога Упор, например, вправо (рис. 4.24) возрастание одной из ошибок (пропуска цели) значительно больше, чем снижение другой (ложной тревоги). Равенство Рдт~Рпр дости­гается При условии Пдт—Ппр = ^с/ш/2, что следует из (4.184), (4.185), (4.188). В этом случае расчет минимально обнаружива­емой энергии сигнала упрощается. Из (4.186), (4.187) путем

Последовательных элементарных преобразований получаем

- ^пр V (N1 + уУш) + л„ УРГХ'

Ых - А^с/Ш УРГ/ (]/'Ых + ма1+УЯш)/ 2,

Nj ^ = NcimV Fryr Nxj% (4.191)

Уут + Nm = (Л^с/ш l^Ty 4. VA^)V2 =

= Frxf (А^с/ш/2)2 + А7'с/ш]//:’/п1/'Л/'ш-{-ЛгШ1 (4.192)

При переходе от (4.190) к (4.191) правая и левая части уравнения (4.190) умножены на разность |/,VT + Лгш — У"А^. Окончательно получаем

Nx^1 РГХ (М:/ш/2)2-j-jVс/шУ"Р(4.193)

Основные формулы теории обнаружения просты и наглядны. Когда шумы усилителя пренебрежимо малы, порог срабатыва­ния можно устанавливать малым: Nn0p^Nx (ведь шумовые вы­бросы в темноте очень редки). Тогда по (4.187) уровень сиг-

* нала задается требованием допустимого пропуска цели

^P==(JVT - A^/yV/yjV,« Л^/уТтуЖ -

^т=^Л'< = - Р^|'(ЛГс/„/2)!. (4.194>

В противном случае, при преобладании шумов ФПУ, полу­чаем тривиальную зависимость iVt — jVc/ui У^-Р/УЛ^. Формула (4.193) суммирует эти два значения! Так что минимально обна­руживаемая величина сигнала Nx оказывается аддитивной - одна ее доля {FNtiwj2) обусловлена только шумами сигнала, другая (NCf, u УТ^/уТУщ)—только шумами ФПУ.

Столь же простым оказывается выражение для минимально обнаруживаемого числа фотоэлектронов, когда РлтфРпр и Я-лт^= Япр. Из (4.189) для значения Nx получается квадратное уравнение, решение которого имеет вид

N, = F^'nl р/2+л„ VFT7jZ+

+ /(ГГ, п1р/2)1 + (ИГ,)^2 ' (4.195)-

Выражение (4.195) пока громоздко. Но в среднем члене под знаком корня можно заменить Лдт-^Ядр» тогда фактически возвращаемся к (4.193):

Nx-Fr^ + NctvVFlTN^ (4.196)*

Даже в самом худшем случае — при FiYJVm«l и асиммет­ричных значениях ппр — 3, ллт = 6 (см. § 3.1) —погрешность при­веденной аппроксимации всего порядка 6 ... 9%.

Какое ФПУ способно зарегистрировать флуктуации сигна­ла? Заготовленных выражений достаточно, чтобы перейти к.

28Г

Численным оценкам — определить уровень шумов ФПУ, при Ко­тором они еще не «забивают» полностью шумы сигнала. В ка­честве предельно допустимого выберем такое значение шума ФПУ (уУшJ, при котором минимально регистрируемый сигнал Л'т возрастает вдвое. Согласно (4.193)

F/y (AWS)2-NchayFГх' [N~],

' ЛГШ< [Лгш1 = (^е/Ш/2)2^Г,74=(3 ... 6)24-0,68/4«

«6.., 24. (4.197)

Здесь и далее для примера выбрано широкополосное ФПУ с двухзвенным фильтром и кремниевым ЛФД {F=4;

= 0,68, Nc/m~6. .. 12). Получили весьма жесткое условие: от ФПУ требуется, чтобы мошность_его шумов была вчетверо ни­же мощности шумов сигнала ДЛГТ2«(Л’с/ш/2)2 (4.194). Конечно, столь малое значение [Л'ш] не может заметно повлиять на суммарный шум jVr-НА'ш] при наличии сигнала (4.187). Так что причина нашего столь жесткого требования в другом — в ложной тревоге. При появлении указанного шума [iVm] возни­кают шумовые выбросы (в отсутствие сигнала), поэтому прихо­дится увеличивать порог и, как следствие, мощность сигнала.

Оценим каждую из составляющих шума ФПУ. Начнем с главной, высокочастотной составляющей. Удерживая ее в вы­ражении для Мл (4.183), получаем

Л^ш = (ешСвхл1дМ)2!УГ2/РГ, г<[Мт}= (N, fml2)2Fr,'№. (4.198)

Естественно, удельный вес ВЧ-шума падает с уменьшением частоты (полосы), так что для заданного набора параметров еш, свх, М всегда существует такая характеристическая полоса.{/у], меньше которой преобладают шумы сигнала:

! < [/у] = (/Т,1' ?Шс/ш/2 я еш С вх) 2/4Г2 =

= [4• 0,68• 1,6 • 10~19 • 100• (6... I2)/2jt*2-10-9-5-10-12]2/4-0,51^

~ (0,8 ... 3) * I О7 Гц. (4.199)

Принятые значения еш, Свх, М (далеко не рекордные) ясны из^выкладки. Как видим, в усилителях с весьма широкой поло­сой около 107 Гц можно достичь значения Л/ш=6 .. . 24 шумо­вых электронов. Конечно, в этом большая заслуга ЛФД: ука­занное число [Ац] получается при пересчете к условному входу ФПУ до каскада умножения (относительно первичного фото­тока). Мощность на входе собственно усилителя в А12=104 раз больше (4.197) — порядка (6 . . . 24) • 104 шумовых электронов.

Поскольку теперь известна полоса /у и соответственно эф­фективная постоянная времени тэ=1/2/у, то известно и число

Регистрируемых темновых электронов за это время, Мо = 10-х3/а = ^1о!2цу. Поэтому теперь можно наложить ограничение темновой (общий) ток /0:

У0 = 2^у^о<2^у[Лгш] =

= 2-1,6* 1(Н9 (0,8 ... 3) ■ Ю7 (6 ... 24) = = (1,5 .. - 23) • 10~и А.

Минимальное значение нагрузки, в свою очередь, опреде­ляется найденным током ФД (2.152):

SHAPE \* MERGEFORMAT

(4.201)

Выполненные оценки показывают, что анализ флуктуаций сигнала имеет отнюдь не чисто теоретический интерес: указан­ные требования к ФПУ достижимы, так что шумы сигнала мо­гут быть сравнимы и даже превышать шумы ФПУ.

Оптимальная фильтрация при учете шумов сигнала. Итак, получены выражения для Лгс/ш с учетом шумов сигнала, найде­но минимально обнаруживаемое число фотоэлектронов ЛГ*. Рас­считать значения Лтс/ш и Л по этим выражениям можно, если задана полоса (постоянная времени) фильтра [у = 1/2тэ. В ши­рокополосных системах полоса определяется из допустимого искажения формы сигнала (§ 4.2), так что ее действительно можно считать заданной. Однако при оптимальной фильтрации сама полоса /у (и форма частотной характеристики) должна выбираться из условия минимизации отношения Мс/Ш. В бес­шумном ФПУ оптимальна большая постоянная времени филь­тра, когда он успевает сосчитать все фотоэлектроны сигнала тэ>2Тс (4.142). При доминирующих белых шумах усилителя максимум отношения А/с/ш достигается при ограниченной посто­янной времени фильтра, равной длительности сигнала тэ = Тс (см. § 3.2). Так возникает очередная проблема — оптимальный фильтр оказывается адаптивным, его частотная характеристи­ка обязана отслеживать соотношение между шумами сигнала и собственно ФПУ, т. е. подошли к постановке одной из сложных нелинейных задач теории обнаружения. К счастью, можно уйти от ее решения:

1. В классическом случае прямоугольного сигнала и белого Шума ФПУ фильтр-интегратор с постоянной времени тэ = ^с не "требует перестройки. Он оптимален при преобладании как шу­мов усилителя, так и шумов сигнала.

2. При доминировании ВЧ-шумов ФПУ также не надо пере­страивать фильтр. Для такого спектра шума оптимальна боль-

Шая постоянная времени тэ«1/я/в (4.57), достаточная и дЛя интегрирования короткого сигнала тэ»Гс.

3. И, наконец^ самый неудобный для нас вариант — сигнал колоколообразный, а шумы ФПУ белые. Вопреки теории по­пытаемся и в этом случае обойтись без перестройки фильтра, здесь опять должна выручить слабая зависимость отношения Л^с/ш от настройки. Возьмем для примера все тот же двухзвен­ный ЯС-фильтр (§4.1 и 4.2), но с некоторой средней постоян­ной времени тэ = етф= Узтс. Это несколько больше постоян­ной квазиоптимального фильтра при белом шуме (тэ = ?"с), но меньше требуемого значения при обнаружении сигнала с уче­том только его собственных флуктуаций (тэ^27'с). Конечно, такая расстройка фильтра приведет к определенным потерям а отношении Лгс/Ш. Необходимые формулы для ее оценки (4.29), (4.66), (4.154), (4.151).

Коэффициент потерь при преобладании белого шума ФПУ

(4,202)

Коэффициент потерь при преобладании шумов сигнала

(4.203)

Вряд ли ради 7% стоит развивать теорию нелинейной филь­трации и тем более синтезировать сложные схемы адаптивных фильтров.

Учет закона распределения шумов, Расчет минимально ре­гистрируемого числа квантов сигнала Лг* все еще не завершен. Пока рассмотрены только два обстоятельства: нестационар-

Ность шума (его возрастание с приходом сигнала) и оптимиза­ция полосы. Самая трудная проблема при обнаружении кван­тованных сигналов третья: задача распределения шумов на вы­ходе ФПУ может отличаться от нормального. А ведь до сих пор расчет_и ошибок Рлт, Рпр, и минимально обнаруживаемого сиг­нала Л'т проводился для нормального закона. Не напрасен ли весь труд?

В § 2.2 и 3.1 отмечалось, что широкое распространение нор­мального закона объясняется тем, что он является законом больших чисел. В рассматриваемой задаче число — это сред­нее число электронов Л'о+А'х, регистрируемых за время на­

Блюдения Тэ - В большинстве ФПУ это число большое. Так, для ФПУ II—V спектральных диапазонов по (4.200) и табл. 2.1 при типичных временах тэл; 10_6... Ю“3 с имеем

ИСА=и ^О = ^0Тэ! д —

= (Ю'9...2-10-4) (10—6... 10-3)/1,6*10-19«

«6-103.. Л012. (4.204)

Из этой оценки следует, что отклик на выходе таких ФПУ представляет собой наложение весьма большого числа импуль­сов Из-за флуктуации можно получить на выходе

ФПУ в момент времени и практически любое значение СЛи(*м). Во всяком случае, в пределах нескольких значений дисперсий вероятность любого значения С/ш достаточно заметна. Дискрет­ность возможных значений очень мала: 1 /ДД0. Все

Это позволяло ранее считать шум случайной произвольной функцией, и большое число А'о приводило к нормальному зако­ну распределения.

Совершенно иная ситуация возникает, когда в интервал на­блюдения Тэ попадает в среднем один электрон и менее:

/о<<7/тэ= 1,6- 10-19/(Ю-6... Ю-9) =

= 1,6-(10-]3... 10-10) А. (4.205)

Подобные значения токов достижимы на кремниевых ФД. Выбранные в этой оценке времена тэ= Ю~6 . . Л 0~9 с соответ­ствуют быстродействию ФПУ на основе таких ФД. Шум на выходе ФПУ, когда он определяется флуктуацией столь малых токов, не может быть функцией любой произвольной формы: ведь теперь возможны только значения, соответствующие двум наивероятным ситуациям: электрон пришел или электрон не

Пришел на интервале наблюдения тэ. Закон распределения шу­мов на выходе ФПУ не может быть нормальным (хотя бы по­тому, что нормальный закон предусматривает возможность ши­рокого спектра значений (/щ). Функция распределения нахо­дится с помощью общего представления выходного отклика как импульсной случайной последовательности — совокупности импульсов М{Н (£м—/*•) со случайным моментом прихода пер­вичного электрона и, а при умножении — со случайной ампли­тудой М<. Строго говоря, закон распределения выходных шу­мов— амплитуды отклика £/ш(/м) —в общем случае отличается от пуассоновского распределения входного шума — числа элек­тронов Лт0-{-Лгт. Это видно из следующего рассуждения. Пусть на входе произошло одно событие — пришел один первичный электрон. На выходе в моменнт 1:^ имеем уже целый спектр возможных событий: в зависимости от момента прихода этого электрона а также значения коэффициента умножения Ш выходное напряжение принимает не одно» а различные значе­ния М{И(1и—А). Появилось еще два «больших числа» — число ВОЗМОЖНЫХ моментов Прихода ti и число возможных коэффи­циентов умножений М{.

Ограничимся случаем, когда указанные факторы не дейст­вуют, рассмотрим классический оптимальный прием сигнала прямоугольной формы на фоне дробовых шумов темнового тока ФД. Так мы в полной мере выявим «ненормальность» пуассо - новского распределения — ее влияние на характеристики обна­ружения. Для указанного случая оптимальным является хоро­шо изученный нами фильтр-накопитель с эффективным време­нем накопления Гн=тэ= Тс, для которого /У= 1 (табл. 4.1). Полагаем также ^=1, иначе говоря, шумы умноже­

Ния и усилителя не рассматриваются (возможность осущест­вления такого режима рассматривается в § 4.4 и 4.5). Выше было показано, что напряжение на выходе фильтра-накопителя пропорционально числу сигнальных и темповых электронов Л-|-Л'0, пришедших на интервале тэ (рис. 4.21), поэтому его флуктуация повторяет пуассоновскую флуктуацию этого числа.

Алгоритм расчета минимально обнаруживаемого сигнала одинаков для любой функции распределения выходных шумов. Как и при нормальном законе, сначала выбирают порог сраба­тывания Л^пор. В отсутствие сигнала произойдет ложное сраба­тывание, если на интервале тэ генерируются Аг0 темновых но­сителей, превышающих порог А/Пор. Естественно, интегральная вероятность всех реализаций Л^^Л'пор не должна превышать допустимую вероятность ложной тревоги Рлт. Для пуассонов - ского распределения получаем

СО —д/

Р{1'о>А’поР)^ 2 е~*":жг<р лт - (4.206)

Затем при выбранном значении Лгпор находят среднее зна­чение сигнала #т— такое, при котором интегральная вероят­ность всех реализаций Аго+Агт<ЛгПОр меньше заданной вероят­ности пропуска цели Рпр:

^'"пор '___ ______

Р(Л^<Л^Ш)р)= 2 е''77^г<Рпр. ЛГ = ЛГ0+ЛГ,. (4.207)

Л^=0

По двум последним формулам рассчитана зависимость мини­мально обнаруживаемого сигнала Мх от уровня темнового тока —числа темновых электронов ЛГ0 (рис. 4.2-5, кривая /)« Здесь же с помощью (4.193) построена аналогичная зависимость в приближении нормального характера шумов сигнала и темно­вого тока (кривая 2). Недостает пока предельных кривых. В отсутствие темновой генерации (М) —0) выбирали порог МПор--=1 и получали минимально обнаруживаемый сигнал Лгт =

Рис. 4.25. Зависимость минимально обнаруживаемого сигнала — числа фотоэлектронов Ых от темпа темновой (и фоновой) генерации Ло (/); различного рода аппро­ксимации и асимптоты (2—5)

= 1п(1/РПр) (4.133) —на рис. 4.25 прямая 3. В другом предель­ном случае (при очень большом темновом токе) его дробовой шум доминирует и ограничивает минимальный сигнал значением

Лгх = Мс/Ш У Ы0 (прямая 4).

Теперь на рис. 4.25 развернута полная экспозиция всех основных особенностей приема квантованных сигналов. Флук­туации гемнового тока становятся решающими при Лго> >(500 .. .1000) — в этой области кривые 1 и 4 неразличимы (рис. 4.2о), минимальный сигнал можно рассчитывать по три­виальной формуле Л^ = ЛГС/ШУ ЛГ0 • При меньшем темпе темно­вой генерации все более и более заметным становится влияние шумов сигнала. В этом диапазоне токов нас ждет самый при­ятный сюрприз: кривые 1 и 2 для пуассоновского и нормально­го распределений практически совпадают вплоть до значений Лг0~1. Число темновых и сигнальных носителей на этом уча­стке еще относительно велико, поэтому пуассоновское распре­деление оказывается достаточно близким к нормальному.

Однако число ЛГ0<1 уже никак нельзя__назвать большим, й неудивительно, что при таких значениях различие кривых / и 2 становится заметным. ФПУ _чутко реагирует на очень малое число темновых электронов Л/о<<£1, которыми, казалось, можно было бы пренебречь. Конечно, шум столь малого числа

1Л¥0 <£1 меньше шума сигнального числа электронов (V Лгт — = УУТТПГГ «3 ... 5) и им можно пренебречь при расчете
пропуска цели, но не при расчете ложных тревог. Даже такой сверхнизкий темп генерации приводит к заметным шумовым выбросам, что заставляет поднимать порог срабатывания ;Упор, а это, в свою очередь, приводит к увеличению минимального обнаруживаемого сигнала ЛГТ.

Сказанное подтверждается следующими выкладками. При столь малом темпе темновой генерации А0<С1 формула (4.206), связывающая этот темп с необходимым порогом АтПСф) упрощается. За ложные тревоги теперь отвечают только им­пульсы с числом электронов Л'о=Лгцор, так как вероятность их появления намного превосходит вероятность появления импуль­сов с большим числом электронов Лг0>Лгпор (4.131). Это дает нам право удерживать в (4.206) один член с АГ0 = ЛГП0Р:

Р(N0>Nmp)= £

Л’о=Лгп0р

__ л£'"°р ^о ’пор

" *„ор' ~ Л'пор' •

Максимально допустимый темп темновой генерации N 0 при выбранном пороге ;Угюр можно записать в явном виде,

Л?„<ЛТл, лор! Лт • (4.209)

Пусть, например, Рлт = 5-10*]о, ФПУ совершенно не обра­щает внимания на темновой ток до тех пор, пока Аг0</>лт = -5-10-Ч Действительно по (4.123) вероятность одноэлектрон­ных импульсов есть р (1) о < 5* 10г1°, так что, сохраняя начальное значение порога АгПОр-=1, получаем вполне допусти­мую вероятность ложных тревог Рат^р (1) = Аго < 5- 10“Ч При большей темновой генерации приходится уже устанавливать порог АгПор2. Он достаточен вплоть до значений А'о< <уг Ь2*(5* Ю^1») жЗ,1* 10"*. При Аг0> 3,1 -10^® следует вновь поднять порог — выбрать А^ор^З и т. д. Так как ЛГ0 и Лгпор яв­ляются целыми числами, то они меняются скачком — на едини­цу. А это приводит и к скачкообразному изменению минималь­ного сигнала №Т} что становится заметным при сверхмалом тем - новом токе.

Для расчета по выбранному порогу Л^ор опять восполь­зуемся «родственными связями» пуассоновского и нормального распределений: число фотоэлектронов в рассматриваемых сиг­налах (А^>7...21) не слишком мало, так что можно на­деяться на «похожесть» указанных распределений. А чтобы при нормальном распределении обеспечить требуемую вероят-

Ность Рцр, надо сохранить зазор между амплитудой сигнала и порогом постоянным — точнее, сохранить постоянным отноше­ние этого зазора к шуму (4.187):

^пр — (£^У—^пор)/^ш — (Л^г ЛГ™Р)Л АГх =

Г/УЪ^сотЛ. (4.210)

Производная от константы обязана равняться нулю:

(1/2УЖ+1/2Л^'2) 6А/х-Мт,/УЯх =0;

ВЛГ, = 2Л^„оР/[1 + (1/Л)1«2ЛГШ1р. (4.211)

Численный анализ для пуассоновского распределения (4.207) показывает, что полученная формула представляет собой аппроксимацию для приращений б N о = Мх — Мсо. 6 N п0? = = А^пор—1- Лишь при уменьшении вероятности ложной трево­ги от 5- 1СИ до 5* 1Он0 несколько сильнее возрастает числен­ный коэффициент от 2 до 2,6. Приращения ^ отсчитываем от начальной точки, когда темновых носителей нет, Д^ПоР => 1 и ;Ухо = 1п(1/РпР) (4.133). Таким образом,

АЛ[да Л/'хо -{- (2 ... 2,6) (ТУпор 1) ^

=1п_Ь +(2...2,6)(ДГпор-1). (4-212>

Рпр

Кривая 5 на рис. 4.25 построена по найденным аналитическим аппроксимациям (4.209) и (4.212).

Итак, справились с последней, самой тяжелой проблемой — учли реальное пуассоновское распределение. Оказывается, при N,>1 для расчета минимально обнаруживаемого сигнала мож­но использовать прежние аналитические выражения (4.193), (4.196), полученные в приближении нормального характера шумов ФД и сигнала. А ведь один темновой электрон в течение длительности импульса 7С—это весьма низкий темп генерации. В современных ФПУ на основе кремниевых ФД шумовой ток обычно не меньше 10-13.. . 10-10 А, так что темп не ниже ука­занного значения Мй~1 (см. (4.206)). Конечно, в специальных разработках и особенно при охлаждении можно ставить рекор­ды— добиваться значений токов ~ Ю-10... 10-14 А и соответ­ственно Аго<С 1 (§ 4.4). Лишь при таком сверхнизком темпе тем­новой генерации проявляются особенности пуассоновского рас­пределения. Пренебрегать этим не стоит — расчет в приближе­нии нормального закона завышает минимально обнаружива­емую мощность сигнала вплоть до 1,8 раз (ср. (4.132) и (4.133)), тем более что и для пуассоновского распределения мы тоже оплучили удобные аналитические выражения (4.209), (4-212). "

Подведем итог. При обнаружении предельно слабых оптических сигна­лов проявляется квантовая природа излучения. Из-за случайности потерь на оптическом пути от источника до ФПУ число фотонов в пришедшем сигнале флуктуирует. Нельзя обнаружить сигналы со средним числом фотонов, меньшим 7... 21, иначе вероятность реализации импульсов с нулевым цнс. лом фотонов будет превосходить допустимую вероятность пропуска цели (5-10~4... 5* 10~10). В общем случае наряду с шумом ФПУ приходится учи­тывать и шум самого сигнала. При этом возникает ряд проблем.

1. Поскольку шум сигнала добавляется только в момент прихода сигна­ла, то общий шум нестационарен.

2. Оптимальный фильтр становится адаптивным. При преобладании бе­лых шумов ФПУ эффективная постоянная фильтра 1х-!> выбирается равной эффективной длительности сигнала Тс. А при преобладании шумов сигнала надо успеть зарегистрировать все фотоэлектроны, поэтому указанная по­стоянная должна быть больше основания импульса —для колоколообразно­го сигнала т-^2Тс.

3. Шумы сигнала на входе подчиняются пуассоновскому, а не нор­мальному распределению, как считалось до сих пор, а их распределение на выходе вообще может быть весьма различным.

Теория разрешает эти проблемы:

1. Нетрудно учесть нестационарность; расчет ложной тревоги надо про­водить, как всегда, для собственного (темнового) шума ФПУ, а при расче­тах пропуска цели добавить к нему шум сигнала. ПоследЕшй соответствует дробовому шуму сигнального тока, усредненного по времени наблюдения т3.

2. Пологая кривая настройки фильтра позволяет избежать адаптации и настроить фильтр на некоторое среднее положение. При этом потери в отно­шении сигнала к шуму не превышают 7% (и это в худшем случае).

3. Пуассоновский характер флуктуаций сказывается лишь при

Сверхнизком темновом токе, когда за время наблюдения тэ генерируется не более одной пары носителей. При большем токе расчет минимально регистрируемого сигнала можно проводить в приближении нормального характера шумов. Прежде этот сигнал рассчитывали, умножая шум ФПУ' У"на требуемое отношение сигнал-шум Л^ш. Теперь действует так же шум: самого сигнала, который учесть очень просто: к Л^с/щ У И Г ^ добавляется член Г /. завися­

Щий от заданной вероятности пропуска цели.РЕЖИМ СЧЕТА ФОТОНОВ *

В § 4.3 было показано, что при очень низком темпе генера­ции носителей и малоинерционном усилителе, когда период между Приходом электронов Тпйр больше эффективной постоян­ной времени усилителя тэ, ток как бы расщепляется на отдель­ные, не наложенные друг на друга одноэлектронные импульсы. Так возникает возможность регистрировать каждый единичный электрон. Фотоприемник может полностью проявить свои спо­собности, заложенные в природе внутреннего фотоэффекта, — стать в буквальном смысле счетчиком, частотомером пада­ющих на него фотонов аналогично ФЭУ, Реализовать режим счета фотонов можно с помощью ЛФД, так как лавинное ум­ножение позволяет подавить шумы усилителя.

Лавинный фотодиод—счетчик фотонов. Попытаемся сосчи­тать фотоны с помощью ЛФД, включив его в обычном линей­ном режиме, когда рабочее напряжение меньше пробивно­го Опр и лавина по существу является линейным предусили - тельным каскадом с усилением, равным коэффициенту умно­жения М.

Счет фотонов при линейном умножении. Принимаем реше­ние о наличии на входе сигнала, которым является один пер­вичный электрон, попавший в слой умножения, когда амплиту­да выходного напряжения превышает пороговое значение:

Ипар^пятиш=пЛтеа1Свх2пУ1//, (4.213)

Напряжение порога Упор устанавливается в /глт=3 ... 6 раз больше шума иш> иначе частота ложных тревог из-за шумо­вых выбросов станет выше допустимого уровня (§ ЗЛ). Для шума в (4.213) оставляем только одну, принципиально неустра­нимую высокочастотную компоненту (4.54). Коэффициент ум­ножения нужно установить таким, чтобы первичный электрон ц создавал сигнал Мс, достаточный для срабатывания порогово­го устройства. Это значение коэффициента умножения назовем пороговым и

^ПОр^с ~ - Л^ПОр^/^Э = ^ порЯ^Уу пор —

=пЛтешСйх2я УГ2/~ (4.214)

В этом параграфе мы следуем нашей традиции — считаем ко­эффициент передачи усилителя Ко единичным, поэтому выход­ное напряжение надо рассматривать как безразмерную (или приведенную ко входу) величину.

Из последнего неравенства следует, что

Л1пор > пятетСахп VГ2/у /?. (4.215)

Полученное выражение задает необходимое значение коэффи­циента умножения. При расчете этого коэффициента сказы­вается специфика счетного режима, обусловленная случайным характером лавины. В книге фактически рассматриваются три ситуации — три уровня сигналов.

Начинали с обычных сигналов: Л/'т~ 102. .. 103 фотоэлектро­нов и более (см. § 1.2, 4.2). Лавинное усиление этой пачки фо­тоэлектронов определялось детерминированной величиной — средним коэффициентом умножения М. И действительно, каж­дый акт регистрации такой относительно большой сигнальной пачки можно рассматривать как прямой эксперимент по оты­сканию среднего значения М. Конечно, умножение для каж-

Дого отдельного электрона из этой пачки случайно: первый

Электрон умножается в раз, второй —в М2 раз, 1-й элек­трон— в Мг раз. Усилитель является накопителем с эффектив - ным временем накопления тэ. Он складывает все вторичные электроны, размноженные на этом интервале Ко­

Эффициент умножения определяем как отношение всех вторич­ных электронов к первичным М= JjM. ilЛ. А это и есть стан­ет

Дартный алгоритм нахождения среднего!. Чем больше выборок (в нашем случае это число электронов в пачке Л^т), тем ближе измеренное значение коэффициента М для этой пачки к своему среднему значению М. Вот почему для относительно большого сигнала (Л/т> 100 .. ,1000) полагаем М&М. Случайный харак­тер размножения сказывается в этом случае при расчете не сигнала, а шума (при умножении темновых носителей).

Второй случай — это более слабые сигналы Лгг~10...100 (см. § 4.3). Для расчета среднего значения выходного сигнала также использовалось среднее значение коэффициента умно­жения М. Однако из-за относительно малого числа Ы? флук­туации М от импульса к импульсу стали заметными, так что при расчете пропуска цели уже нельзя было не учитывать ко­лебание выходного сигнала относительно своего среднего зна­чения. Случайный характер лавины учитывался не только в тепловом шуме, но и в шуме сигнала, где ее представлял шум - фактор Б.

И вот теперь третья, самая тяжелая ситуация — умножение всего-навсего одного электрона! Здесь не в состоянии помочь закон больших чисел, так как Л^=1. Случайный характер вы­ходного сигнала полностью повторяет случайный харак­

Тер коэффициента умножения Л1, так что дальнейший анализ невозможен без функции распределения для этого коэффици­ента. Вероятность одному электрону размножиться в М раз р(М) рассчитана в [61, 89]. Распределение р(М) для одного электрона оказывается значительно «хуже», чем для пачки, состоящей из большого числа электронов. В последнем случае вероятны только значения М в окрестности среднего М. А для одного электрона вероятность распределения р{М) очень раз­мывается. Наиболее вероятны малые значения М~ 1,2,3, ;

Чем больше значения М, тем меньше вероятность их появления. Поэтому для каждого отдельно взятого носителя всегда обес­печивать требуемое умножение Л1пор невозможно. Получили стандартную для теории обнаружения ситуацию (см. § 3.1): есть конечная, весьма значительная, вероятность реализаций, для которых М<аМП0р. В этих случаях пороговое устройство не сработает, что приведет к дополнительному снижению кванто­вой эффективности в счетном режиме. В квантовой эффектив­ности ЛФД Г|Г}сч' появляется новый множитель Т)сч'—эффек­тивность счета. Она равна сумме вероятностей всех реализаций с коэффициентами Л]^Л1пор. Простое аналитическое выраже­ние для такой интегральной вероятности получается при одно­сторонней лавине, когда размножается только один тип носи­теля [61]:

«»Р. ^сч = Р(М>'Мпор) = ехр [(Жлор - 1)/М]. (4.216)

Из (4.216) вытекает, что для счета фотонов с необходимой эффективностью г|сч надо обеспечить среднее значение коэф­фициента М, превышающее требуемый для каждой реализации коэффициент Мпор в следующее число раз:

М»1; I —ч = М/Л1„0р«г 1/Мсч«

' * 1/(1 — г|',)= 1/[1 — (0,8 ... 0,9)] = 5 ... 10. (4.217)

Эта оценка отражает неприятные особенности счетного ре­жима. Из-за флуктуации умножения (размытой функции Р (Л1пор)) появляются дополнительные потери в квантовой эф­фективности Чтобы эти потери были приемлемыми,

Т1сч/да0,8 ... 0,9, приходится выбирать среднее значение Л1 очень большим — при односторонней лавине в 5... 10 раз боль­ше умножения Мщэр, необходимого для каждого одиночного электрона.

Полоса усилителя. Чтобы шум усилителя не мешал реги­страции единичного электрона, надо выполнить условие

(4.215) . Примем для численной оценки; у = 5..Л0; Плт“ = 3... 6; еш=2 нВ-Гц~1/2; Свх^5 пФ; М = 200. Это достаточно высокий, но еще не рекордный уровень параметров. Осталось выбрать только полосу усилителя fy. Чем меньше эта полоса, тем меньше мешают ВЧ-шумы усилителя счету электронов. По

(4.215) , (4.217) максимально допустимое значение /у при про­чих фиксированных параметрах равно

/у < 7^ (яМ/чп-Л1ещСъуп)1 =

2

= —10-19-200/(5 ... 10) (3 ... 6) 2-10-9*5.10"1?я]2»

«0,6-103... Ю4 Гц. (4.218)

Возможности ЛФД в обычном линейном режиме оказались ■более чем скромными: он способен «вытащить» одноэлектрон - ньгй сигнал над шумом лишь весьма узкополосного усилителя. Так что в принципе ЛФД считает электроны, но очень медлен­но. При «эволюционном» развитии — улучшении параметров М, еШ) Сих — не исключена возможность повышения полосы на один-два порядка, но и этого будет недостаточно для быстро­действующих систем. Поэтому пошли «революционным» путем:

Коль скоро широкая полоса требует практически бесконечного умножения М (4.215), то обеспечим его — будем работать при пробое!

Счет фотонов в режиме пробоя. Установим на ЛФД^рабо­чее напряжение £/р>£/пр. При попадании электрона в область высокого поля инициируется лавина, ток начинает возрастать теоретически до бесконечности. Реально же ток ограничен не­линейными эффектами: поле экранируется размноженными но­сителями и становится недостаточным для ударной ионизации. Максимальная плотность тока ЛФД, при котором экранируется поле, оказывается порядка 10... 100 А/мм2 [59, 90], так что в ЛФД с диаметром площадки около ОД.. .0,2 мм амплитуда импульса тока составит /А~ 1 . .. 40 мА. Такой режим работы при Ур>6гПр можно назвать ключевым, включение («зажига­ние» импульса тока) происходит от первичного электрона. ЛФД «принял весь огонь на себя»: при столь большой ампли­туде тока можно практически не беспокоиться о шумах усили­теля — использовать низкоомную входную нагрузку и широкую полосу. Так, при входной нагрузке усилителя £!вх« «50... 100 Ом, включенной последовательно с ЛФД, напря­жение импульса составит

^а==^ех/а=(50... 100) (10~3... 4 ■ 10~2) = 0,05 ... 4 Б. (4.219)

А шум усилителя намного меньше, даже если он шумит как сопротивление /?ш» 1 кОм и полоса /у*= 1 ГГц:

Иш = у 4ЛГ^шЛ/, = 1^1,6.10-». 1№-0,68.1?*»

Ж 100 мкВ. (4.220)

Особенности токовых импульсов в ключевом режиме (при пробое). В линейном режиме ЛФД импульс тока, наведенный одним первичным электроном, имеет детерминированную фор­му, длительность определяется постоянной времени ЛФД (если измеряем импульс тока самого ЛФД) либо постоянной времени ФПУ ( если измеряем выходные импульсы ФПУ). Случайной является амплитуда импульсов — она пропорциональна случай - ному значению коэффициента М. В режиме пробоя все наобо­рот: амплитуда детерминирована (определяется током насыще­ния), длительность импульса случайная. Есть хоть и очень ма­лая, но конечная вероятность всем носителям вылететь из ла­винной области без ионизирующего столкновения, тогда лавина самопроизвольно погасится. При разработках первых ЛФД, которые были неоднородными по площадке, такие импульсы наблюдались на микроплазмах (т. е. локальных областях с ранним пробоем), поэтому их часто называют микроплазменны- мн [59].

Случайная длительность импульса не годится для счетного режима: пока лавина не погасится («ключ» не разомкнется),

ДФЦ не способен сосчитать следующий квант. Так прищли к необходимости создания схем принудительного гашения им_ пульса — пассивной или активной [91, 92]. В пассивной схеме последовательно с источником смещения ир включается боль­шое сопротивление яв. При возникновении в ЛФД импульса тока /А на этом сопротивлении создается падение напряжения 1АЯн■ Подбирая его номинал таким, чтобы *УР—/лЯн<£/пр> сбрасываем напряжение на ЛФД ниже пробивного и гасим ла-’ вину. Постоянная времени импульса определяется /^С-постоян­ной "схемы. В активной схеме гашения отрицательная обратная связь строится по-иному: импульс на выходе ФПУ автоматиче­ски управляет напряжением на ЛФД, и напряжение опять-та - ки сбрасывается до значений ниже пробивного. Эта самая быстродействующая и совершенная схема для счетного режима.

Квантовая эффективность счета в режиме пробоя. К сожа­лению, даже в этом режиме эффективность счета меньше еди­ницы. Ведь существует конечная вероятность р(М= 1,№) того, что первичный носитель пролетит весь лавинный слой тол­щиной IV без размножения. Эта вероятность легко рассчиты­вается. Введем обозначение: р( 1, х^-йх) —вероятность первич­ного электрона пролететь часть лавинного слоя (от его начала _д: = 0 до точки х--с1х) без ударного столкновения. Это событие можно разбить на два последовательных. Электрон должен сна­чала долететь без столкновения до точки х, вероятность р{ 1, х). А затем еще пролететь без столкновений отрезок с1х, вероят­ность р( 1, йх). Естественно, р( 1, х--с1х)=р( 1, х)р( 1, (1х).

Согласно определению коэффициента ударной ионизации а ве­роятность ударного столкновения на отрезке (1х равна айх, так что вероятность «не столкновения?> 1— айх = р(, йх). Отсюда получаем простое дифференциальное уравнение

Р( 1, х--йх) =р (1, х)р(, йх) —р (1, х) (1—ас1х); [р(1, х + с1х)—р( 1, х)]1йх + ар(, х) =0, с1р( 1, х)!йх--ар{ 1, х)=0.

Решая его при начальном условий р( 1, 0) = 1, получаем

Р(1, х) =ехр(—а*); г|Сч'< 1— р(1, Щ - = 1—ехр (—аи7).

В принципе и вторичные носители п, генерированные после нескольких ударных столкновений, могут вылететь из лавинно­го слоя без дальнейшего размножения. Эти события также снижают квантовую эффективность счета, поэтому в (4.222) вводится знак неравенства. Но чем больше произошло первых Ударных столкновений, чем больше п и тем меньше вероят­ность того, что все п носителей сумеют вылететь из лавинного

Слоя без ударного столкновения. Поэтому наиболее вероятнь? два состояния лавины: или она вообще не включится (с веро­ятностью по (4.222)), или она нарастает до тока насыщения.

Из (4.222) следует, что чем выше перенапряжение = ир—ипр и коэффициент а, тем выше квантовая эффектив­ность счета. Особенно большим должно быть перенапряжение ЛС/ в ЛФД с ^-/м-р-структурой, а также на материалах с близ­кими значениями коэффициентов ударной ионизации электро­нов и дырок а «р. В первом случае это обусловлено большой толщиной 1-слоя, поэтому для дополнительного (сверхпро-

Бивного) поля требуется большое перенапряжение Во втором случае причина иная: при напряжении пробоя мало значение ай7 —оно порядка единицы [59, 61]. А по (4.222) для получения высокой квантовой эффективности требуется су­щественно большее значение а^яь2, т. е, само приращение по­ля должно быть большим. На практике обычно работают с пе­ренапряжением ДС/=10 .. .40 В [92, 93]. Для работы в режиме пробоя при столь больших перенапряжениях требуется созда­ние специальных ЛФД с особо высокой степенью однородности всех его свойств по площадке. Самые небольшие вариации по глубине и степени легирования, дефекты структуры могут при­вести к появлению микроплазмы — включению только локаль­ного участка перехода. Другая неприятность — большая кон­центрация свободных носителей в лавинной области, что уве­личивает вероятность их захвата на ловушки.

Частота темнового счета и принятие решения о наличии сигнала. Наряду с фотоэлектронами ЛФД считает и темновые электроны. Частота прихода темновых электронов с учетом квантовой эффективности счета ^сч' определяет частоту темно­вого счета

/сч — Ч/Т пер — Лсг/о/Я-

Надо подчеркнуть, что здесь ток /о — только та составля­ющая, которая поступает в слой умножения (неумножаемые токи утечки исключаются). Частота темнового счета однознач­но определяет частоту ложных тревог: /лт = /сч. Приходим к

Очередному жесткому требованию, предъявляемому к ЛФД, работающему в счетном режиме, — требованию сверхмалых то­ков. Поэтому в таких ЛФД добиваются их рекордных значе­ний: при комнатной температуре 70 = /т«: 1(Н4 А, при охлажде­нии /Т^1СН« А. Это соответствует частоте темнового счета

/сч= (0,8 ... 0,9) (1<Не... КН4)/1,6-10-19:

«5-102.. .-5-Ю4 Гд.

В отдельных системах (например, рефлектометрах, измеря­ющих качество и дефектность в°локонно-оптических линий) та­кая частота может быть допустима. Однако в большинстве оп­тико-электронных систем (обнаружители, наведение, связь) та­кая частота недопустима. Поэтому для принятия решения о сигнале надо использовать стандартный алгоритм (см. § 3.1 и 4.3): вести счет на интервале тэ, равном длительности сигнала Тс, И, когда сосчитанное число электронов будет превышать некоторое пороговое значение АгПор, принимать решение о нали­чии сигнала. Чем больше число темновых электронов Мь тем выше устанавливается порог ЛГпор (4.206), (4.208), (4.186).

Как видим, перед приемом сигнала надо измерить лТ0. Для по­вышения точности время измерений следует выбрать достаточ­но большим, а для исключения возможной температурной и временной нестабильности Лго использовать синхронный счет, чередуя счет электронов на интервалах, когда сигнала нет и когда возможен его приход [94]. Это усложняет схему — ведь в аналоговом линейном режиме достаточно было просто отфильтровать постоянную составляющую.

Все эти трудности счетного режима приходится преодоле­вать ради основной задачи — улучшения пороговых характери­стик.

Пороговые характеристики в режиме счета фотонов. Какой выигрыш в пороге чувствительности дает счетный режим? По­становка такого вопроса сначала вызывает недоумение. Ведь в § 3.2 отмечено, что поиск схем лучше оптимального фильтра — это поиск вечного двигателя! Пороговые характеристики опти­мального фильтра превзойти нельзя. Да и вообще любой' фильтр-усилитель можно рассматривать как некоторый эффек­тивный накопитель, интегратор, счетчик (§ 4.1). Вспомним при­ем сигнала прямоугольной формы на фоне дробового шума то­ка. В этом классическом случае оптимальный фильтр самым непосредственным образом считает электроны. Он складывает - отклики от всех электронов, пришедших на вход в интервале* Ти^Хэ^Тс, выходной сигнал пропорционален числу входных электронов (§ 4.3). В чем же тогда своеобразие рассматри­ваемого метода счета?

В фильтре-интеграторе считается общее число элек­тронов, пришедших на вход фильтра за время тэ. В схеме счета импульсов с пороговым устройством считается число- актов прихода элементарных импульсов за это время (амплитуда импульса на результат счета влияния не оказывает). В отсутствие умножения эти алгоритмы идентичны: каждый импульс на входе состоит из одного электрона. Но си­туация качественно меняется при умножении. В каждом эле­ментарном /т-м импульсе содержится уже Mi вторичных (раз­множенных) электронов. Так что фильтр-интегратор выдает

* V:

■’пор

12 3 * 5 ±

Ю

Рис. 4.26. Фильтр-накопитель в аналоговом режиме (о> считает все вторичные электроны ЛФД, в счетном ре­жиме (б) — количество элементарных импульсов (пер­вичные электроны)

Сигнал, пропорциональный общему числу вторичных ЛЧ

Электронов 2 Мх, а в схемах счета по-прежнему опреде­ляется число актов прихода — число первичных элек­тронов (рис. 4.26).

Как видим, счет счету рознь. В фильтре-накопителе к флук­туациям числа входных электронов добавляются флуктуа­ции умножения. В счетных схемах благодаря пороговому устройству коэффициент умножения становится безразлич­ным— лишь бы он превышал пороговое значение Мпор. В по­давлении шумов умножения и состоит смысл счетного режима. Пока не будут разработаны «бес­шумные» ЛФД со сколь угодно большим коэффициентом М, до тех пор будет выгодно для подавления шумов лавины приме­нять счетный режим.

Величина минимального регистрируемого сигнала в счетном режиме фактически была рассчитана в § 4.3 (рис. 4.25, кри­вая /). Именно счетный режим позволяет подавить шумы уси­лителя, не внося шумов умножения, и регистрировать предель-
до малые сигналы на фоне собственных дробовых шумов тем­пового (и фонового) тока ЛФД.

Насколько >х>дшаются пороговые характеристики при умно­жении? При строгом расчете следует учитывать статистику раз­множения. Однако в § 4.3 было показано, что вплоть до весьма малых темновых токов, когда за время наблюдения генерирует­ся всего один электрон, можно проводить расчеты в приближе­нии нормального закона. При указанном токе в сигнале со­держится порядка 60 электронов (кривые 2, рИс. 4.25, точка /Г0=1). Это вполне достаточное число для нормализации умно­жения [89, 95]. Поэтому для сравнения обычного линейного лавинного режима со счетным можно пользоваться формула­ми (4.193) и (4.196), полученными в приближении нормального распределения. Из этих формул следует, что устранение шумов умножения в счетном режиме приводит к улучшению поро­говых характеристик в У Р... Т7 раз, где Р— шум-фактор ла­вины. Даже для самых малошумящих кремниевых^ ЛФД при /г = 4 минимальный выигрыш составит около 1/^ = 2 раз— весьма ощутимую величину. Эту численную оценку в каждом конкретном случае надо уточнять. Выигрыш может быть не­сколько меньшим (из-за потерь при счете Т]сч'г|сч//) * а может быть и большим (при более шумящей лавине, сверхмалом тем-

Новом токе Лг0<£; 1) -

Счетный режим — не альтернатива оптимальному фильтру, а один из методов его реализации, позволяющий считать пер­вичные электроны. Схему счета можно построить как фильтр, но цифровой: после порогового устройства (с уровнем порога Л1Пор) поставить счетчик, выдающий число пришедших электро­нов Л'т, затем решающее устройство с порогом Мпор. При ^Лгпор оно должно принимать решение о наличии сигнала. Уровни темнового шума У^А'о, порога ЛгПОр и сигнала обыч­ным образом определяют ошибки приема — ложную тревогу и пропуск цели. В принципе можно формировать и необходимую оптимальную (квазиоптимальную) импульсную характеристику 0> усложнив счетчик: складывать импульсы от первого порогового устройства с весом Н —^), зависящим от момен­та прихода (момента счета) этого импульса

Временное разрешение. После прихода первого электрона на выходе усилителя ФПУ возникает импульс с некоторой эф­фективной длительностью Тэ. В широкополосном усилителе при режиме перенапряжения длительность Та определяется време­нем гашения лавины (7?С-постоянной входной цепи в пассив­ных схемах, постоянной обратной связи — в активных). При узкополосном усилителе длительность Тэ может определяться самим усилителем: Тэ=хэ~ 1/2/у. На период Тэ включается по­роговое устройство. Приход на этом временном интервале вто­рого электрона состояния порогового устройства изменить не

Может, и этот электрон не зарегистрируется. Поэтому два пер­вичных электрона могут быть сосчитаны, только если они раз­несены во времени более чем на эту постоянную времени Тъ. Временное разрешение 7Э является еще одним специфическим параметром счетного режима.

А какое временное разрешение необходимо? Все зависит от того, сколько темповых электронов генерируется за время действия сигнала Тс, какой поэтому необходим порог Лгпор и соответственно сколько нужно зарегистрировать электронов Л^^Л^ор. Возьмем для конкретности оценок темновой ток /0«2- 10-ь А, вероятности ошибок Рлт = Рлр = 5' 1СН0. Период следования темновых электронов при выбранном токе будет равен Тпер~ 9//0 ~ 10-4 с. За период действия импульса при его типичной длительности в высокочастотных системах ГС~ = 10-э... 10~6 с генерируются

ЯГ0 = /оЗД = Гс/Гпер = (1 о-9... 10-6)у 10-4 =

10~5... 10-2 (4.225)

Тепловых электронов. Поэтому порог срабатывания по (4.208) должен быть равным Л^ор — 2. .. 5. Чтобы принять решение о наличии сигнала, необходимо зарегистрировать не менее Лгп0^ сигнальных электронов. К приходу последнего из них должны быть зарегистрированы предыдущие Л'ПОр—1 электронов, на это уйдет время (Л'пор—1) Тэ. Если последнему электрону «не по­везет» и он попадет в тот же временной интервал, то такой электрон не будет сосчитан. Устройство обнаружит лишь «счастливый» электрон, который придет на свободном интер­вале Тс—(ЛТпор—1) Т'э (не занятом счетом предыдущих элек­тронов). Так получили еще одну причину снижения квантовой эффективности в счетном режиме, теперь уже не из-за флуктуа­ции умножения, а из-за конечности времени счета:

ТпеР>Тс; 1];ч = [Гс-(,Упор~1)Г9]/Гс - . .

= 1 —- (Л^ор— 1) Тэ/Тс. (4.226у

Принимая разумным опять значение гц^0,9, получаем следую" щее допустимое временное разрешение:

1 ■ Лсч ~ (А^пор ~ 1)ТЪ/Тс; Тэ ^ (1 'Псч) Тс/(Л^пор 1) —

-0,1 Гс/(1 ... 4)-= ту (10 ... 40). (4.227/

Не исключено использование счетного режима при длинных импульсах с, когда число электронов, генериро­

Ванных за время действия импульса,

ЛГ0=Гс/7пер=(Ю-3... 1)/Ю-4= 10 ... 104 (4.22В)

Намного больше единицы. Флуктуации в этом случае нормаль­ны, поэтому порог (превышение над постоянным уровнем ЛГ выбирается в Плт раз выше шума (4.182):

Алпор/^о = (^о + «лт]/ЛА7о)/ Л/0= 1+п„1Умй =

= 1 10 . .. 104^2 ... 3.

За каждый период прихода одного темнового электрона Гпер надо зарегистрировать по крайней мере еще один, сиг­нальный электрон, чтобы принять решение о наличии сигнала. Заменяя в (4.227) Гс-^пер и подставляя ЛгПОр=2...3, полу­чаем

Гпер«Гс; Гэ < (1 - л;ч)/(1 ... 2) Гпер =

= ТПер/(Ю * * * 20). (4.229)

Требование к полосе усилителя. Из (4.227), (4.229) для вре­

Менного разрешения вытекают следующие требования к полосе усилителя:

Гвер»Гс; /у^1/2Гв - :

= (10 .. . 40)/2Гс = (10 ... 40)/2 (10-9 ... 10-6) =

= 5-10е... 2-1010 Гц;

Тпер"^ ТС, /У^(10...20)/2Г пер —

— (10 ... 20)/2-10~4 = (5 ... 10) • 104 Гц. (4.230)

Из-за необходимости разрешить во времени каждый элек­трон полоса частот ФПУ в счетном режиме должна быть зна­чительно шире, чем в традиционном аналоговом режиме. Если

В аналоговом режиме полоса /у порядка полосы сигнала 1/2Гс

(а при оптимальной и квазиоптимальной фильтрации и замет­ном ВЧ-шуме — существенно меньше), то в счетном она на порядок и более должна превышать эту полосу 1/2Тс. При очень длинном импульсе полоса /у вообще определяется не дли­тельностью сигнала (1/2Гс), а значительно более коротким пе­риодом следования темновых импульсов (1/2Гпер). Поскольку особенно жестки требования к временному разрешению при обнаружении коротких импульсов, то полоса усилителя в этом случае должна быть особенно широкой — необходим СВЧ-уси - литель. Естественно, (4.230) определяет и требования к быст­родействию ЛФД. Эксперименты, однако показали, что основ­ные неприятности на пути повышения разрешения связаны не с необходимостью применения ВЧ - или СВЧ-техники или огра­ниченным быстродействием ЛФД, а с прилипанием носителей.

Прилипание носителей. Решив одну задачу (обеспечив большое усиление), создали новые трудности. При перенапря­жении концентрация носителей заряда в лавинной области становится очень большой, достаточной даже для экранировки поля. При столь больших концентрациях носители захватыва­ются на ловушки в ОПЗ. Когда лавина погасится, все подвиж­ные носители вынесутся полем из области пространственного заряда и на ЛФД вновь подается напряжение выше пробивно­го, «отсидевшийся» на ловушке носитель через некоторое Вре­мя тл опять выбрасывается в зону, инициируя новую лавину. Возникает ложная тревога (возрастает скорость темнового счета). Борьба с ловушками, снижение постоянной тл являются также специфическими требованиями при разработке ЛФД, работающих в счетном режиме. Для снижения ложной тревоги, обусловленной высвобождением носителей с ловушек, особенно полезными оказываются все те же схемы активного гашения. Длительность гасяшего импульса должна выбираться больше постоянной времени освобождения ловушки Тэ= (3 . . . 10)Тл. Поскольку при охлаждении постоянная времени тл возрастает, то есть некоторая оптимальная рабочая температура ЛФД: ниже нее очень велика постоянная гл, а выше — темновой ток /т. Эта температура определяется типом ЛФД (концентрацией и типом ловушек и генерационных уровней), а также требова­ниями конкретной системы по скорости темнового счета и раз­решению. Для кремниевого ЛФД значение этой температуры составляет 200 К [93].

Достижимое временное разрешение определяет и динамиче­ский диапазон схемы счета фотонов. Поскольку на счет каж­дого электрона тратится время 7Э, то за заданную длитель­ность Гс можно сосчитать не более ^тах = 7с/Т3 электронов. Если тл«Ю~8 с; Га = 5-10-8 с, то уже для 7С^10"6 с имеем Л'тшах = 20. При коротких сигналах ограничение начинается практически с пороговых значений Л. Поэтому, если требует­ся не только обнаружение, но и измерение величины сигнала, надо параллельно использовать оба режима — счетный и обыч­ный аналоговый.

Подведем итог. При низком темпе генерации носителей ток как бы рас­щепляется на отдельные, не наложенные друг на друга импульсы, индуци­рованные одним первичным электроном, что дает возможность считать каждый электрон в отдельности. Для их счета применяются специальные режимы и схемы. Например, на ЛФД подается напряжение выше пробив­ного, после инициирования лавины первичным электроном лавина принуди­тельно гасится (напряжение на ЛФД сбрасывается); применяются широко­полосные усилители (почти воспроизводящие форму лавинного импульса); •для регистрации импульса, инициируемого одним электроном, используют ■пороговое устройство. При таком способе регистрации значение коэффици­ента умножения и его флуктуации роли не играют, происходит подавление. шумов лавины. В этом и состоит преимущество счетного режима по сравне­нию с обычным аналоговым. Счетный режим характеризуют специфическими параметрами: частотой темнового счета, обусловленной темновым током; вре­менным разрешением - временем, которое тратится на счет одного электро­на (определяется временем гашения лавины, полосой усилителя, временем высвобождения ловушек от захваченных при пробое носителей); квантовой эффективностью счета (дополнительные потери — пропуск фотонов при их счете — возникают при наложении импульсов друг на друга, а также при пролете носителя через лавинный слой без ударного столкновения, вероят­ность чего хоть и мала, но конечна).

Работать в счетном режиме могут только самые совершенные ЛФД___________ с

Высокой однородностью пробоя по всей площадке, малой концентрацией ловушек, рекордно низким уровнем темнового ток