ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ХЕМИ0СМ0ТИЧЕСК0Е СОПРЯЖЕНИЕ

Механизм фосфорилирования в окислительно-восстановитель­ной цепи до сих пор нельзя считать точно установленным. Важ­ное значение для его исследования имеет теория хемиосмотиче - ского сопряжения, развитая Митчеллом. Эта теория была пред­ложена впервые в 1961 г. [41]. Ее подробное изложение содер­жится в обзорных работах Митчелла [42—45] и в монографии Скулачева [46].

Не пользуясь непосредственно представлениями неравновес­ной термодинамики, Митчелл оперирует понятием сопряжения, необходимым при рассмотрении открытых систем. Очевидно, что сопряженные процессы универсальны в живой природе. В любой биохимической реакции, катализируемой ферментом, имеется

Сопряжение между электрон­ными и конформационными пе­рестройками. В системе, содер­жащей жидкие фазы, разде­ленные мембраной, возникает сопряжение между химически­ми реакциями и мембранным транспортом, именуемое Мит­челлом хемиосмотическим со­пряжением. Мембрана играет роль сопрягающей системы. В столь общей формулировке идея хемиосмотического со­пряжения не содержит чего - либо нового по сравнению с представлениями об активном мембранном транспорте, изло­женными в гл. 2 и 3. Особенности подхода Митчелла состоят в следующем.

Предлагается конкретная модель сопряжения дыхания с фосфорилированием, исходящая из феноменологических сообра­жений.

Рассматриваются главным образом равновесные соотно­шения между факторами, определяющими сопряжение.

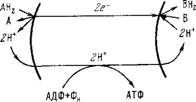
Рис. 6.12. Принцип хемиосмотиче­ского сопряжения окисления и фос­форилирования по Митчеллу. і — внутренняя, е — внешняя стороны мем­браны.

Конкретная модель представляется схемой, показанной иа рис. 6.12 [46]. Донор водорода АН2 (например, аскорбат) окис­ляется ^переносчиком электронов (например, цитохромом с) у внешней стороны мембраны. Два электрона переносятся через
мембрану по дыхательной цепи и посредством цитохромоксидазы передаются акцептору водорода В, т. е. кислороду. Акцептор присоединяет два протона из внутренней фазы митохондриаль - ного матрикеа. Создается градиент концентрации протонов — их избыток во внешней и недостаток во внутренней жидкой фазе. Вследствие этого происходит перенос протонов через мембрану в противоположном направлении, в результате чего и реализует­ся фосфорилирование — синтез одной молекулы АТФ приводит к поглощению двух протонов из внешней фазы и выделению двух протонов в матрикс. Митохондриальная мембрана работает как топливный элемент, в котором разность электрохимических потенциалов создается за счет окислительно-восстановительного процесса.

Равновесные термодинамические соотношения определяются тем, что разность свободных энергий в системе слагается из хи­мической и осмотической (транспортной) работы:

АО = ДОхим + АСосм, (6.16)

Где

Д«о;м = I V/(M7 - И?) + X v; - ц°). (6.17)

Сумма по / есть сумма по всем продуктам, сумма по і—по всем реагентам. ц® — стандартные химические потенциалы, vj, V,- — соответствующие числа молей. Если переносится лишь один компонент, то обобщенная сила, действующая на него, есть

ДІЇ = - ДСосм/v. (6.18)

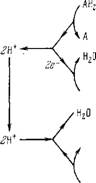
Схему, показанную на рис. 6.13, можно считать состоящей из двух «петель» (рис. 6.13, а) — окислительно-восстановительной (дыхание, о/в-петля) и гидрогенизационно-дегидрогенизацион - ной (дефосфорилирование, г/д-петля). Сопряжение обоих про­цессов посредством протонного транспорта показано на рис. 6.13,6. Согласно (6.17) имеем в равновесии

Д(ін+ = - Д0осм/2 = ^Дф, (6.19)

Где SF — число Фарадея, Дг|з — разность потенциалов (в воль­тах). В процессах о/в и г/д

- (А«оем)о/в = - (А«осм)г/д = 2 ДДн (6.20)

И в сопряженной системе

ДОосы = - (А«осм)о/в 4 (А«осм)г/д. (6.21)

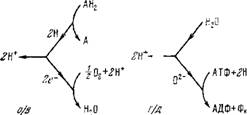
Полный электрохимический потенциал каждого компонента в системе выражается формулой

= + + (6.22)

<0

Где р — давление, — молярный объем, zt — заряд компонента, — электрический потенциал, с, — концентрация (активность).

JOi + Ztt*

АТФ+<?Н+

АДФ + Ф„

А)

Рис. 6.13. Детализация схеїмьі Митчелла.

А — петли о/в и г/д; 6 — сопряжение обоих процессов.

Полная обобщенная сила, приводящая к равновесию 1-го компо­нента во внешней фазе и в матриксе, равна

Д(хг = Уг Ap + zt&~ &i> + RTA\nCi, (6.23)

Причем можно показать, что член VtAp относительно мал. Для протонов

ДДН = Л\|з + RTA In сн+, (6.24)

Или, переходя к рН,

Д(хн = ^"Аф —2,3/?ГДрН. (6.25)

Протонодвижущая сила

Д/^Дф —ZApH (6.26)

(6.27)

Состоит, таким образом, из двух вкладов (Z = 2,3 RT/&~). При равновесии между внешней (е) и внутренней (і) фазами Д£ч = 0 и пз (6.23) следует

, с? Aib = In-*-,

С

Т. е. уже известная формула для равновесия Доннана — Нернста (см. стр. 123).

С перемещением протонов через мембрану связано опреде­ленное значение ее энергетической емкости, т. е. буферного дей­ствия. Емкости фаз е и і равны

_ dH+ dHf

Где сШ+ означает число протонов, добавляющихся в соответ­ствующую фазу. Буферная емкость мембраны В определяется числом протонов ДН+, переходящих из фазы е в фазу і на еди­ницу понижения рНе по отношению к рН,, или

L/B=l/Be+l/Bt.

ЛН+ = — В АрН. (6.30)

Аналогичным образом, электрическая емкость сопрягающей мембраны равна

С-

Где Де+ есть число положительных зарядов, переносимых из фазы е в фазу і. При С = const

Ае+ = С Лг|х (6.32)

Работа, совершаемая при генерировании разности рН обрати­мым переносом протонов, равна

-АрН

ГДрн= \ ZApHrf(AH), (6.33)

-АрН»

Где Д рН° — равновесное значение А рН и Д рН' = А рН — А рН°. При постоянной буферной емкости В

Гдрн< = '/2 ZB {(АрН)2 - (АрН0)2}. (6.34)

Аналогичным образом получаем выражение для работы, совер­шаемой при генерировании A\f> обратимым переносом протонов

Гдг = 72С{(Аф)2-(Дг|э0)2}. (6.35)

Причем

Если В = const, то

Если установлено равновесие для протонов, то протонодвижу- щая сила А/= 0 (ср. (6.26)), Дф° = £ДрН° и полная энергия

WAf хемиосмотической системы, связанная с электрическим и химическим компонентами этой силы, равна

Wsf = w \рн' + W дг = '/2 С (Аф)2 + >/2 ZB (ДрН)2 -

- 72 Z (ZC + В) (АрН0)2. (6.36)

Интегрируя от 0 до — АрН', находим выражение W\f через АрН' и Аф' = Дф —Аф°:

Wlf = '/2 С (Аф')2 + ■/, ZB (АрН')2. (6.37)

Соответственно, уравнение (6.26) можно переписать в виде

А/ = Аф' — Z АрН'. (6.38)

В митохондриях (из печени крысы) площадь сопрягающей мемб­раны оценивается в 40 м2 на 1 г белка [47]. Электрическая ем­кость при частотах порядка мегациклов составляет около 1 мкФ/см2 [48]. Отсюда находим С а 0,4 Ф на I г белка или 4 мкэкв-В/г белка. Значение В « 12 мкэкв• В/единица рН на 1 г белка. Принимая величину А/= 270 мВ, получаем W,\t = = 0,15 мкэкв - В на 1 г белка при АрН' = 0 и WAf = 7,2 мкэкв - В на 1 г белка при Аф' = 0. Свободная энергия гидролиза АТФ составляет около 10 ккал/моль или около 0,44 экв-В. Сле­довательно, W\f соответствует 0,35 мкмоля АТФ на 1 г белка при АрН' = 0 и 17 мкмоль АТФ на 1 г белка при Аф'= 0. Бо­лее точные оценки дают соответственно 0,24 и 12 мкмоль АТФ на 1 г белка. Если синтез АТФ сопряжен с переносом двух за­рядов электрона, что следует из экспериментально найденного отношения Ф„/2е - = 1 для каждого места фосфорилирования, то необходимое значение Аф' действительно оказывается не менее 200 мВ, т. е. при толщине мембраны порядка 100 А напряжен­ность электрического поля в ней не менее 2-Ю5 В/см. Значение Дф' = 200 мВ эквивалентно вкладу АрН' = 3,5 в общую прото - нодвижущую силу А/.

Разность потенциалов Аф в митохондриальной мембране мо­жет возникать не только за счет транспорта протонов, но и за счет транспорта других ионов, происходящего одновременно. Так, для ионов К+ в равновесии справедливо соотношение Нернста

Дф = гДрК, (6.3"))

Или

D (ДК+) _ D

D( ДгИ <6-40)

Где D — эффективный буферный дифференциал для К+, опреде­ляемый как

П _ d (ДК + ) U d (АрК) •

Соотношение между Аі|з и полным смещением зарядов, вызван­ным перемещением всех ионов через мембрану, есть

ЈD(Ae+) = Cd(At|>), (6.41)

И связь между Лг|) и полным перемещением зарядов (за исклю­чением перемещения, вызванного ионами К+) дается выраже­нием

£ d (Ае+) — Cd (Лг|)) — d (ЛК+) — Cd (А-ф) + - j - d(Ai|j). (6.42)

Кроме К"**

Ионы к+ считаются здесь находящимися в равновесии. Величина С + DZ~X есть полная эффективная емкость. Ее значение может сильно возрастать, если мембрана проницаема для данного иона.

Если мембрана непроницаема для ионов Н+ и і порознь, но возможен их совместный транспорт в одном направлении, т. е. симпорт (symport) по Митчеллу, то условие равновесия запи­шется в виде (v — стехиометрические коэффициенты)

Vj Арі - f - vH+ ДрН == 0. (6.43)

Если реализуется антипорт (antiport), т. е. движение ионов і в направлении, противоположном транспорту Н+, то

Vj Арі — vH+ АрН == 0. (6.44)

Симпорт с Н+ установлен, в частности, для некоторых анионов: Ар (дикарбоксилат2") + 2 АрН = 0, Ар (трикарбоксилат3-) + 3 АрН = 0. Возможны и более сложные ситуации, например, Ар (фосфат3-) + 2 АрН + АрК = 0.

Антипорт должен осуществляться для Н+ и катионов.

Соотношения между АрН и Аф можно представить в виде (см. стр. 301)

= (6-45)

Ет-^' №.46,

Суммирование проводится по различным типам реакций, в ходе которых происходит транслокация протонов и других заряжен­ных частиц. При постоянных В я С получаем выражения, ана­логичные (6.30) и (6.32):

£дН+ = - ЯДрН, 2>е+ = САг|-. (6.47)

Второе уравнение можно переписать в виде

£ЛН+ + £А1+ = САф, (6.48)

Где Л1+—члены суммы Ае+, отличные от АН+. Из выражений (6.26), (6.47) и (6.48) следует

ДрН с - V ДІ+Mf

~ ~дГ= Л в, г • (6-49)

При равновесном распределении протонов А/ = 0 и

У (д/+)°

Выражение, содержащее лишь отклонения от равновесия, имеет вид

(6.51)

Z ДрН' С - £ (А/+)'/Д?

Af С + B/Z

Таким образом, относительные вклады —ZApH и Аф в А/ зави­сят лишь от С, В и от числа смещаемых непротонных зарядов. Вообще говоря, сумма (А/+) отрицательна вследствие движе­ния ионов через мембрану по электрическому градиенту, т. е. в направлении, противоположном движению протонов. Эта сум­ма минимизируется при симпорте протонов и анионов или при антипорте протонов и катионов. Напротив, увеличение переноса ионов в присутствии, скажем, валиномицина (см. стр. 151) должно увеличивать отрицательное значение А/+ и, таким об­разом, увеличить вклад —ZApH' по сравнению с Аф'.

Не ограничиваясь приведенными соотношениями, Митчелл рассматривает кинетику генерации и затухания АрН' и Аф' в не­которых простейших случаях. Цель этого исследования состоит, в частности, в интерпретации изменений рН, возникающих после достижения равновесия под влиянием импульса окисления — восстановления или гидролиза АТФ. Такой импульс может быть создан добавлением соответствующих веществ.

Полная протонодвижущая сила А/ состоит из специфического потенциала Лф', определяемого электрическими свойствами про­тонов, и разности —ZApH', определяемой их кислотными свой­ствами. Сила А/ стремится восстановить электрическое и кис­лотно-основное равновесие. Митчелл предполагает существова­ние линейной связи между силой и потоком, т. е. рассматривает близкую к равновесию ситуацию. Полную ионную проводимость, включающую протонную, можно описать уравнением

= - gin Mf'- 2 АрН'), (6.52)

Где п — число зарядов иона, эффективная протонная проводи­мость представлена как доля 1/п от полной проводимости, г. е. g = (l/ti)g, и члены, отвечающие ZgApH для других ионов, счи­таются пренебрежимо малыми. Опыт дает на 1 г митохоидри - ального белка g— 1,7 мкэкв/(В-с). Для протонной проводимо­сти имеем

D (АН+) ,

—Jt—= — gAf. (6.53)

Из уравнений (6.26), (6.29) и (6.53) следует, что

= Дг|/_2Дрн'), (6.54)

И из уравнений (6.31) и (6.52) находим

C^p - = g(ZApW-nAV). (6.55)

Допустим, что ДрН' и Дф' генерируются импульсом окисления — восстановления, причем скорость переноса Н+ постоянна и равна

(А&р.) =_в(1Ш) =k

^ dt Л/в V dt Л/в

V dt JQlB

Полные скорости генерации ДрН' и Дг|/ даются выражениями

В d (АрН') = gm, _ z ДрН/) _ ^ (б>56)

С d — g(Z ДрН/ - П Аф') + к. (6.57)

Решения этих уравнений при начальных условиях ДрН' = Дф' = = 0 при t = 0 имеют вид

^' = С^ [-Р (" - М-ЧМ]• (6-59)

Где q — Z/B - j - п/С, ш = дД2 + г, s = Z/B — п/С, г = 4Z/CB. При стремлении —ZAрН' к стационарному значению Аф' возра­стает до максимума, а затем падает до нуля. Если мембрана про­ницаема практически лишь для ионов Н+ или ОН - и g = g или

П = 1, то решения (6.56) и (6.57) не могут быть получены в виде (6.58) и (6.59). В этом специальном случае уравнения (6.56) и (6.57) не независимы и их можно переписать в виде

D (ДрН') _

(6.60) (6.61)

D (ДрН') dt

С d (Аф')

Dt

В

Интегрирование (6.60) и (6.61) дает

- Z ДрН' =

BgO/C + Z/B)

(6.63)

Zk

[1 — ехр (— g(\/C ZjB)t)\ (6.62)

Аф' = Ц - С (- Z АрН').

В этом случае генерация Аф' и —ZApH' происходит синхронно. Время затухания обеих величин до половины исходного значе­ния определяется в основном величиной С. Для митохондрий оно составляет около 1,5 с. Вообще говоря, временной ход —ZApH' зависит от значения п, при больших п это время со­ставляет около 80 с.

Дальнейшие подробности, относящиеся к теории Митчелла, изложены в работах [42, 44]. На языке линейной неравновесной

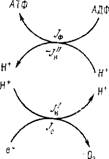
Рис. 6.14. Схема потоков в химиосмотической мо­дели.

ОнК< ) « і

А

'фН

Ф ф Н ~ ^фН^ф I ^Н

Ill

Термодинамики (см. § 6.3) соответствую­щие соотношения можно записать на ос­нове упрощенной схемы, приведенной на рис. 6.14 [34]. В области / имеем (ср. стр.294)

/' = L' АДН + L'sf'

(6.64)

}О = LoH ААн + L,

И в области II

L!'stl+L>'Aii

(6.65)

В области / окисление вызывает транс­порт протонов в направлении, противо­положном АДн, в области // спонтанный поток создает фосфо­рилирование. Общий поток протонов

J Н = }'п + /н,

Или

(6.66)

Основное предположение теории Митчелла состоит в том, что коэффициент прямого сопряжения окисления и фосфорилирова­ния равен нулю (£фО = 0). Иными словами, если Арн поддер­живается постоянным, то фосфорилирование должно быть неза­висимым от окисления, и наоборот. В частности, при АДн = 0 разобщение полное и /ф = 0, если = 0 при любом значении /о, а также /0 = 0, если si"= 0 при любом значении /ф.

Теория Митчелла — феноменологическая теория, не рассмат­ривающая механизм процесса и не учитывающая электронно - конформацнонные свойства митохондриальной системы. Тем не менее, эта теория позволяет прийти к ряду конкретных выводов, подлежащих прямой экспериментальной проверке. Вместе с тем подлежит проверке и предполагаемая в теории Митчелла бли­зость процесса к равновесию.