ТЕРМОДИНАМИКА И ЭВОЛЮЦИЯ
Теория Эйгеиа согласуется с термодинамикой нелинейных необратимых процессов (см. гл. 2 и 8). При постоянных потоках стационарное состояние характеризуется относительным минимумом производства энтропии. Такому состоянию соответствует доминирование отобранных гиперциклов. Если произошла стохастически значимая мутация, состоящая в возникновении мутанта с большей селективной ценностью, то это означает появление отрицательной флуктуации производства энтропии, и система переходит в неустойчивое состояние. Далее, система переходит в новое стационарное состояние с большей упорядоченностью, т. е. с меньшей энтропией. Изменение энтропии в эволюционирующей системе показано на рис. 9.4 [44] (ср. стр. 421).
Ясно, однако, что изменение энтропии или количества информации, вообще говоря, не может быть критерием эволюции, для которой существенно не количество, но ценность информации.
Смысл теории Эйгена состоит не в объяснении реального хода эволюции на Земле, но в демонстрации принципиальной возможности и, более того, необходимости селекции и эволюции гиперциклов. Демонстрация эта основывается на четко формулируемых физических соображениях и показывает значение ценности информации, выражаемой через измеримые величины.
Пригожин, Николис и Баблоянц провели более общее рассмотрение эволюции в терминах теории устойчивости [53] (см. также [132, 169]).
Допустим, что имеется п взаимодействующих веществ Хг- (і = 1, 2, . . . , п) с достаточно высокими концентрациями Имеем для открытой системы
Х^РЦх *„) + <^>(* *„)• (9.29)
499
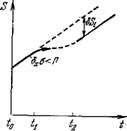
Рис, 9.4. Зависимость энтропии от времени для процесса отбора при постоянных общих потоках мономерных единиц. В интервале осуществляется стационарное состояние (а = = const), интервал t[t2 — область неустойчивости, прн t > to возни кает нозое стационарное состояние
Первый член описывает поток вещества (скажем, в форме мономеров) из окружающей среды, второй — реакции внутри системы. Считаем Z7? постоянным и систему однородной. Предположим, что уравнение (9.29) имеет по крайней мере одно асимптотически устойчивое решение; это значит, что все п
корней характеристического уравнения имеют отрицлтельныё действительные части.
Допустим теперь, что случайно возникают мутанты веществ Хг, т. е. их ошибочные копии Yj (/= 1, ..., s) с концентрациями у j. Порядок уравнений (9.29) возрастает на s. Если s=l (один мутант), то характеристическое уравнение увеличенной системы будет содержать дополнительный член порядка є. При малом є характеристическое уравнение будет иметь п + 1 корней, причем я корней будут близки к корням системы (9.29). На устойчивость стационарного состояния увеличенной системы будет влиять лишь новый корень <й„+1, который может зависеть от є либо как
Со„+1~е->, (9.30)
Если поправочный член является множителем в члене, содержащем (п 1)-ю степень со, либо как
Со„+1 ~ 8, (9.31)
Если появление Yj добавляет постоянный член в характеристическом уравнении. В результате в обоих случаях могут возникнуть корни с положительной действительной частью. Малое возмущение системы (9.29) может привести к существенному изменению ее стабильности. В случае (9.30) это изменение будет очень быстрым, в случае (9.31)—очень медленным. В случае (9.30) эволюция Y описывается уравнением
Гу = 0({х), у, г), (9.32)
И уравнения (9.29) принимают вид ({*} — совокупность всех переменных Xi)
Xi = F!({x}) + Fi({x}, у, е). (9.33)
При е = 0 последние уравнения превращаются в (9.29). В случае (9.31) уравнения (9.32) и (9.33) переписываются в виде
Г/^И + еОЛМ, У, е), (9.34)
= Я ({*}) + <F „>({*}) +b(F21)({X), у, в). (9.35)
Эти уравнения описывают эволюцию системы посредством изменений устойчивости системы при добавлении новых веществ. В частности, может возникнуть состояние, в котором вид Y будет доминирующим.
(9.36),
Рассмотрим случай (9.30). Введем новую временную переменную т = t/ssi>_ t и перепишем уравнение (9.32) в виде
%r = G({x}, у, е).
Мы видим, что уравнения (9.32) и (9.33) описывают эволюцию системы в разных шкалах времени. Уравнения (9.32) и (9.36) представляют быструю продукцию нового вещества Y при практически постоянных значениях {х}, уравнения (9.33)—медленное изменение {х} после того, как у достигло своего стабильного значения, отвечающего G({x}, у, 0) = 0. Тем самым селекция должна происходить весьма быстро. С термодинамической точки зрения ситуация эквивалентна представленной на рис. 9.4 — избыточная продукция энтропии, созданная флуктуациями, т. е. добавочная диссипация, становится отрицательной. Энтропия и ее продукция являются стохастическими функциями флуктуирующих переменных, и термодинамические величины получаются путем усреднения этих функций. При появлении нового вещества Y можно построить функцию состояния, связанную с вводимой таким образом диссипацией. Для устойчивой системы эта функция имеет минимум. Эволюция возникает, если функция имеет более чем один экстремум или седловую точку. Это — вариационный принцип, характеризующий эволюцию. После точки перехода продукция энтропии возрастает, так как система переключается на путь быстрого синтеза вещества Y,
В случае, характеризуемом со„+і ~ є (см. (9.31)), уравнения (9.34) и (9.35) описывают (при неустойчивости) медленную эволюцию вещества Y к новому режиму. Сравнение с уравнением Эйгена (9.14) показывает, что фактор є можно интерпретировать как среднюю скорость мутаций, причем неустойчивость непосредственно определяется ошибками копирования. В случае соп+1 ~ є-1 (см. (9.30)) роль мутаций состояла во введении связей между старыми и новыми переменными. Эволюция через неустойчивость определялась появлением новых элементов, как, например, новых ферментов.
Положим в уравнении (9.34) G! = 0, т. е. допустим, что новое вещество производится только мутациями. Исходная система (9.29) может стать неустойчивой, если G2 — возрастающая функция у вблизи ({хо}, У> 0), где х0 — решения исходной системы, В точке перехода добавочная диссипация, вводимая Y и соответствующими изменениями xit становится отрицательной. Наиболее интересно положение, относящееся к случаю (9.30),— когда система, эволюционируя к новому устойчивому режиму, увеличивает свою диссипацию. Такое поведение противоположно поведению вблизи стационарного состояния, не сильно удаленного от равновесия и устойчивого по отношению к флуктуациям. После достижения нового режима система вновь стремится уменьшить свою диссипацию.
Эти представления можно иллюстрировать простой кинетической моделью [53, 54]. Рассмотрим открытую систему, в которой имеется поток мономеров двух видов (скажем, нуклеотидов)
А и Ь. Внутри системы, в «ящике», происходит полимеризация, образуются цепи Ai и В. Реакция образования At протекает через промежуточную форму R, соответствующую объединению, мономеров а в линейный ансамбль, образованный нехимическими взаимодействиями. Такой ансамбль может переходить з другое состояние R*. Имеем реакции
Па R, R^R*
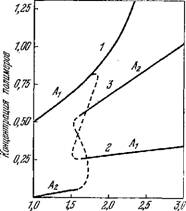
Концентрация мономеров
Рис. 9.5. Влияние флуктуаций на продукцию полимеров.
Объяснения в тексте. Концентрации — в произвольных единицах.
Sb^±B.
Как только образовались Аь R* и В, включается автокаталитический цикл, в котором Ai действует как матрица для синтеза,
В из Ь и В действует как матрица, превращающая R* в Aj. Далее А! и В диффундируют из «ящика» или дезактивируются. Имеем
A! + sb^± Ai + B, B + R*^±A, + B A, + Bj±AB,
Д диффузия /11 >■)
G диффузия ^
Численные решения, основанные на данных, полученных при изучении образования полинуклео - тидов, показывают, что при определенных значениях констант скоростей возникают множественные стационарные состояния полимеризации, отвечающие большому или малому содержанию полимеров в системе.' На рис. 9.5 кривая 1 представляет изменение А і с концентрацией мономера. Изменение R* представляется сходной кривой.
Представим себе теперь, что случайные флуктуации непрерывно создают ошибки при образовании Аь катализируемом В. Возникает новый вид А2. Полимер А2 может катализировать синтез нопого вещества Е, например, примитивного фермента из г мономеров сорта с. Будучи созданным, Е катализирует далее как собственную продукцию, так и продукцию А2. В конце
§ 9.5. термодинамика и эволюция
Концов Е и А2 уходят из «ящика». Имеем
Ek
Rc-f А25±Е + Аз, В + R* + Е ^ В + А2 + Е, гс + А2 + Е^2Е + Аз,
G диффузия ^ Д^ диффузия ^
Эта система реакций описывает нелинейное сопряжение между А2 и Е, которое тем сильнее, чем больше R*. А\ и R* зависят от стационарного состояния, достигнутого при полимеризации. Результаты численных расчетов показаны на рис. 9.5. При малой концентрации мономеров доминируют полимеры Аь Это стационарное состояние могло бы продолжаться (кривая 1), но флуктуации создают новый полимер А2 и катализатор, усиливающий продукцию А2. При критическом значении концентрации мономеров возникают неустойчивости (пунктирные кривые), и система резко переключается в новое стационарное состояние, в котором доминируют полимеры А2 (кривые 2 и 3). Переход вызван как мутациями, так и появлением катализатора Е. Первые служат триггером неустойчивости, второй определяет остроту перехода. В этом смысле модель объединяет случаи (9.30) и (9.31). Описанное эволюционное поведение системы связано с ее автокаталитическими, нелинейными свойствами.
Термодинамика дает общее понимание эволюции. В частности, возрастание диссипации может привести к эволюционной обратной связи, создающей путь к новой неустойчивости, к дальнейшей эволюции системы. Наибольшая приспособленность при этом не обязательно означает наибольшее размножение.
Конечно, такой детерминистический анализ должен быть дополнен и уточнен стохастическим (см. стр. 491).
Очевидно, что приведенное рассмотрение не дает еще теории эволюции в истинном значении этого слова. Однако оно раскрывает физический смысл эволюции и имеет безусловное иллюстративное значение.
503
Следует отметить, что качественные соображения сходного характера были высказаны ранее Молчановым [12], указавшим, что статистическая термодинамика, как таковая, применима лишь к ранним стадиям эволюции. Смысл этого утверждения состоит в том, что «применимость статистических представлений уменьшается в процессе эволюции, так как уменьшается число частиц» — скажем, из мономеров образуются полимеры. Теории Эйгена и Пригожина имеют уже не термодинамический, но
Кинетический характер. Роль термодинамики сводится, в конеч* ном счете, к анализу неустойчивостей.
Изложенная в §§ 9.3—9.5 область теоретической физики находится на начальной стадии своего развития. Однако пути этого развития намечены, и понимание добиологической эволюции вышло за пределы качественных спекуляций.