НЕЛИНЕЙНЫЕ ХИМИКО-ДИФФУЗИОННЫЕ СИСТЕМЫ

Рис. 8.14. Фазовые траектории на плоскости X, Y.
Результаты численного интегрирования уравнений (8.61) с А = 1 В = 3 при начальных значеннях: л=У = -0(1), Х=У = 1 (2), Х=10, Г = 0(3), Y= 3 (4).
Системы, рассмотренные в предыдущем параграфе, были точечными, или сосредоточенными. Происходящие в них события не зависели от положения в пространстве. Рассмотрим теперь распределенные системы. Пространственная нетермодинамическая упорядоченность, т. е. пространственная диссипативная структура, может возникать в гомогенной системе.
Впервые проблема устойчивости по отношению к диффузии была исследована в классической работе Тьюринга, имеющей примечательное название «О химической основе морфогенеза» [30]. Эта работа и исходящие из нее исследования школы Пригожина ставят своей конечной целью дать модельное толкование важнейших биологических явлений, определяющих онтогенетическое развитие (см. гл. 9).
Дополним уравнения (8.61) членами, описывающими одномерную диффузию вдоль координаты г. Имеем (см. [1, 3, 115, 116, 123])
} (8.66)
= А + Х2Г - ВХ - X + D^ д*Х
Dt п "г" л 1 ил л ~ дг2 ^ = BX-X2Y+Dy-^. j
Вещества X и Y характеризуются разными константами одномерной диффузии Dx и DY. Ищем решение системы (8.66) в виде концентрационных волн
X = + 6Х ехр (Ш + іг/А), -) У = У0 + бУехр(<в< + іг/Л). J ('
Здесь Л есть длина волны, характеризующая пространственную неоднородность, ЬХ Х0, б У Уо - Получаем характеристическое уравнение
+(Л2+ 1-fi-f а + Ь)Х + Л2(1 + а) + (1-В)й + а6 = 0, (8.68)
Где
А = Dx/A2, b = D у/Л2.
При Л->оо система становится однородной и уравнение (8.68) совпадает с (8.62).
Уравнение (8.68) характеризуется двумя типами неустойчивости. Первая возможность соответствует равенству нулю множителя при К и положительному значению суммы свободных членов. Имеем условие
Йкр < В < В"р,
Где
В'кр = 1 + А2 + а + Ь, В:р = (А2 + Ь)(\+а)/Ь.
Вторая возможность соответствует равенству нулю суммы свободных членов. При этом один из корней (8.68) обращается в нуль.
Условие нестабильности имеет вид
Длина волны, при которой В'К9 минимально, есть Л-*оо и шіпВ'кр = 1 - f А2. Минимум Вкр (Л) имеется при Л2 = (DxDy)h/А, он равен
Шіп В'кр = [l + Л (Dx/Dy)''2]2.
Неустойчивость возникает, когда В возрастает до меньшего из этих двух значений. При равенстве коэффициентов диффузии
Шіпйкр = 1 + А2 < min Blр = 1 - f A2 - f 2А
И реализуется предельный цикл. Напротив, при достаточно малых Dx/DY происходит нарушение симметрии и возникает пространственная неоднородность. Для В, немного большего В |>р,
Л
I
I
І1
І11І
Ж
I =1
53534853489101534823232353022323485348235302
О 0,5 1
Пространство, ороазв. вд.
Рис. 8 15. Стационарное распределение вещества в результате нарушающей
= 8.10"
= 1,6 ■ 10 £>у
Т. е. тіпВкр»5, шіп Вкр«7,7 [2].
Флуктуации с Л, близкой к Акр, усиливаются, и система покидает стационарное состояние. Затем она стабилизуется в новом стационарном состоянии, уже пространственно неоднородном. На рис. 8.15 показано вычисленное стационарное неоднородное распределение X и У в пространстве для системы (8.66), воз-
Симметрию неустойчивости [2]. Концентрации X, Y на границах области поддерживаются равными гомогенным стационарным значениям Х = 2, У = 2,62. Численные значения параметров: Л = 2,00, В = 5,24,
Никающее за пределами неустойчивости, нарушающей симметрию.
Переходя от уравнений (8.55) к уравнениям (8.61) и (8.66), мы пренебрегли обратными реакциями и положили k = 0. Тем самым система далека от равновесия. Диссипативная структура, изображенная на рис. 8.15, стабилизована потоком энергии и вещества из внешнего мира. Она характеризуется меньшей энтропией, чем исходная стационарная гомогенная система, — осуществлен порядок через флуктуации.
В приведенных соотношениях константы скоростей прямых реакций приняты равными единице. Если отказаться от этого упрощающего предположения, то Акр и £кр окажутся завися-, щими от Dx, Dy и от химических констант. Неустойчивость есть кооперативный эффект, в котором участвуют и химические реакции и диффузия.
Подробный математический анализ ситуаций, возникающих в случае двух реагирующих компонентов, способных к взаимной диффузии, проведен в работе [31].
Реальная модельная или биологическая система не является однородной системой с постоянными граничными условиями. Сами концентрации веществ А и В, фигурирующие в качестве параметров, зависят от г и t. Рассмотрим ту же систему (8.66), считая для простоты В постоянным, но учитывая изменения концентрации А [2]
Dt
Ищем совместное решение уравнений (8.66) и (8.69), удовлетворяющее граничным условиям
А(0) — А (/) = А, Х(0) = Х(1) = Х, У (0) = Г (/) = Р (0 < г < I).
Перечислим свойства этого решения [3]:
Вблизи термодинамического равновесия имеется единственное устойчивое стационарное состояние.
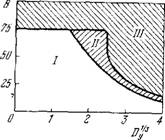
Рис. 8.16. Свойства рассматриваемой автокаталитической системы при заданных A, DA, Dx и при DB -» оо как функции В и Dy (в произвольных
Единицах). / — область устойчивого стационар - _ _ ного состояния, 11 — область мо-
Qf-2 • иотоиного возрастания флуктуа - ций, III — область усиливаемых ко - (8.69) лебаиий.
Вдали от равновесия возможны различные ситуации, представленные на диаграмме (рис. 8.16).
В области II диаграммы термодинамическая ветвь становится неустойчивой по отношению к флуктуациям химического состава. За порогом В начальные отклонения от стационарного состояния усиливаются и в конце концов приводят систему в новое стационарное состояние, соответствующее регулярному распределению X и Y (рис. 8.17).
Для DB Da DY ~ Dx термодинамическая ветвь неустойчива, но система переходит в пространственно неоднородное состояние, периодически зависящее от времени. Возникают концентрационные волны, распространяющиеся в реакционном объеме и отражающиеся от границ системы. В каждой точке происходят колебания концентрации.
Пригожин и Николис отмечают, что пространственная локализация вещества является вероятным механизмом стабилизации диссипативной структуры по отношению к изменениям химического окружения. Локализованные структуры характеризуются производством больших количеств отдельного вещества в течение короткого времени в ограниченной области пространства. Таким образом, система обладает регуляторными свойствами. Концентрационные волны являются вероятным механизмом распространения и передачи информации в форме химических сигналов, а стационарные локализованные
Структуры могут хранить информацию [2].
5. При конечных значениях DA описанные структуры локализованы внутри реакционного объема. Их границы, а также периоды определяются значениями величин А, В, Dx и т. д. независимо от начальных условий. При DA, DB^>-°о структуры захватывают весь объем. Если Dx, DY очень велики по сравнению с химическими скоростями в области III (см. рис. 8.16), то пространственные зависимости исчезают и система осциллирует везде с одной и той же фазой. Амплитуда и частота колебаний определяются свойствами самой системы. Реализуется предельный цикл, периодическое движение устойчиво.
Подробное рассмотрение систем такого типа проведено в [1,2, 123].
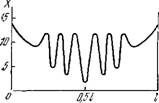
Рис. 8.17. Локализованная стационарная диссипативная структура, возникающая в области II предыдущей диаграммы.
Есть все основания думать, что можно подойти к пониманию упорядоченности живых систем на основе кинетического анализа нелинейных химико-диффузионных процессов, приводящих к упорядоченному поведению на макроскопическом уровне. Во
всяком случае, мы не располагаем пока другими подходами при изучении этих явлений. «Биологические часы» сводятся к «химическим часам», что отчетливо демонстрируется периодическими ферментативными системами, в частности системой гликолиза (см. § 8.7), а также периодичностью других биологических явлений (см. § 8.8).
Весьма обещающими для биологии являются исследования множественных стационарных состояний, возникающих в кооперативных химических и физико-химических системах (см. [7]). На основе таких исследований построены модели биосинтетических процессов в клетке и нелинейных мембранных систем (см. § 8.9). Кинетические кооперативные явления, в частности деполяризация возбудимой мембраны аксона, всегда имеют нелинейный характер.
Другой аспект изучения нелинейных процессов применительно к биологическим явлениям связан с проблемами эволюции, биологического развития. Эти проблемы рассматриваются в гл. 9.