ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ И ФАЗОВЫЕ ПЕРЕХОДЫ

Нелинейные системы характеризуются фазовыми портретами с различными особенностями, в частности, с устойчивыми и не­устойчивыми особыми точками. Нелинейные системы способны переходить из одних состояний в другие под действием малых флуктуаций, нарастающих до макроскопического уровня.

Шлёгль впервые показал, что в ряде случаев поведение не­линейной системы оказывается подобным фазовому переходу первого или второго рода [117]. Возникновение новой структуры в распределенной нелинейной системе имеет такой характер. Неравновесные переходы, определяемые неустойчивостями, дав­но известны в гидродинамике (например, переход от ламинар­ного к турбулентному течению и эффект Бенара, см. [1, 115,

116]).

Рассмотрим вслед за Шлёглем [117, 118] автокаталитические реакции (ср. стр. 415)

А + 2Х

С.

К.

■—2

Зх, в + х

Скорости реакций равны

(8.121)

V, = kxAX2-k-xX\ v2 = k2BX — k-2C,

Положим для простоты k. i = 1, k\A = 3 и обозначим k2B = р, k-чС = у. Скорость изменения концентрации X равна

X = v]-v2=-X3 + 3X2 — p>X + y. (8.122)

Стационарные состояния отвечают условию X = 0 или

Y = - ЗХ2 + pjf. (8.123)

Кривые vW, представляющие эту зависимость, показаны на

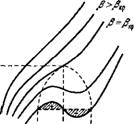
X/ Х3-7 Х2

Рис. 8.45. Фазовый переход пер­вого рода в автокаталитической химической реакции.

1.

Х

Рис. 8.45. Уравнение X = 0 имеет три корня. Эти корни совпадают при критическом значении р — = Ркр:

1, Ркр==3,

Три различных вещественных и положительных значения корней Х2 > Х3 > Х[ возможны лишь при р < 3. Решения Xi, Х2 устой­чивы, неустойчивый корень находится на убывающей ветви у(Х). Получилась картина, весь­ма сходная с диаграммой со­стояния газ — жидкость. При этом концентрация X играет роль плотности V-1, величина у соответствует давлению р, а вели­чина р — температуре RT. Имеем

(8.124)

V3

Р 3,1 Y = V-T7T+

Уравнение Ван-дер-Ваальса имеет вид

RT о_

(8.125)

Р— V — b V2

B2RT - jTT-

Или в вириальной форме

(8.126)

RT, bRT ■

V2

Полная аналогия получается для вириального уравнения со­стояния

Р = RT/V — fli/V2 + (8.127)

С вириальными коэффициентами ai и а2, независимыми от тем­пературы.

Таким образом, в рассматриваемой автокаталитической си­стеме при р < ркр происходит переход между двумя устойчи­
выми стационарными состояниями и Х2, подобный фазовому переходу первого рода. Внешним условиям, задаваемым р и у, отвечают два конкурирующих состояния Xi и Х2. Этот переход не связан с нарушением симметрии. Можно показать, что усло­вие Максвелла — равенство площадей + и — на рис. 8.45 — со­блюдается.

(8.128)

А® (Л)

(8.131)

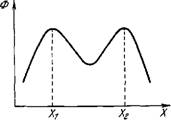
Рис. 8.46. Сосуществование фаз Xi и Х2.

(8.133)

Y = P'

*.,2=l=F(3-f5)\ *з=1.

Если одновременно с химической реакцией происходит диф­фузия компонента X (система является распределенной), то при постоянных значениях А, В, С получаем

X = у (*) + DV2X, причем y W можно представить в виде

У W'= Ж'ф Ф W = 'А*4 ~ + '/г?*2. (8.129)

Ф(^) играет роль некоторого потенциала. Считая диффузию од­номерной, перепишем уравнение (8.128) в виде

(8.130)

Стационарные состояния удовлетворяют уравнению

D4^ =

Дг2 дХ

Это уравнение сходно с уравнением, описывающим движение массы в потенциальном поле, если 2 играет роль времени, а X — коор­динаты. Имеется стационарное со­стояние, в котором сосуществуют две фазы Х\, Х2, причем Х-+Х\ при z —> ОО И Х-*~Х2 при 2 ->—OO. Xi и Х2 соответствуют относительные максимумы Ф(^). В стационарном состоянии происходит перемещение «массы» D от одного максимума Ф(Х), при котором эта масса по­коилась, к другому максимуму, в котором она также достигает со­стояния покоя. Это возможно лишь в том случае, когда значе­ния Ф в обеих точках одинаковы (рис. 8.46):

Ф(^,) = ф(^2). (8.132)

Мы получили условие сосуществования двух фаз, которое фиксирует значение у. Как показывает Шлёгль, из условия (8.132) следует

Наряду с фазовыми переходами первого рода нелинейные автокаталитические процессы могут приводить к неравновесным переходам, подобным фазовым переходам второго рода. Рас­смотрим реакции

А + X 5± 2Х, В + X ї± С.

Их скорости равны

V2 = k2BX — k-2c.

(8.134)

V^kiAX-k-tX2,

Положим kiA= 1, k-t = \, k2B = $, k-2C — у. Находим

+ + + (8Л35)

X > 0 при малых X и X < 0 при больших X. Следовательно, стационарное состояние, отвечающее X = 0, устойчиво. В этом состоянии

Y = Z2-(1 — $)X = - f{X). (8.136)

Ч1;

(8.137)

X

Если Y — О, т0

— Р при Р< 1, при 1.

Такое поведение величины X характерно для фазового перехода второго рода, скажем, перехода из ферромагнитного в парамаг­нитное состояние. В этой аналогии X играет роль параметра упорядоченности (намагниченности), у — напряженности маг­нитного поля, р— температуры. Значение р = рКр = 1 отвечает точ­ке Кюри. При р < ркр происходит нарушение симметрии. В критиче­ской точке малые флуктуации воз­растают до макроскопических зна­чений. Имеем, согласно (8.135),

Y + f(X)-,

ЬХ.

ДХ

Или

ДІ

(8.138)

6* = - (1/т) 6Z, (8.139)

Где т-1 = 2Х — (1 — р). При у —*0 и т-'->|1-р|. Но

Отсюда следует, ЧТО в критической точке Р= Ркр = 1, т —* оо.

На рис. 8.47 показаны кривые зависимости X от р при раз­личных значениях у-

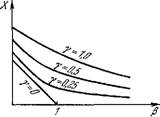
Рис. 8.47. Фазовый переход второго рода в автокаталити­ческой химической реакции.

Отсюда

X ■■ ЬХ--

Эти аналогии, найденные Шлёглем, весьма поучительны. По­ведение модельной химической системы, подобное фазовому пе­
реходу, свидетельствует о ее кооперативных свойствах в истин­ном смысле этого слова, о переходах типа «все или ничего». Как мы видим, модели биологических систем, описывающие самоор­ганизацию, имеют именно такой характер. Это — триггерные системы, совершающие переходы в результате малых флуктуа - ций. Соответственно можно думать, что идея о неравновесных фазовых переходах как механизме биологических явлений яв­ляется многообещающей. Уже получены некоторые интересные результаты. В работе [119] исследованы неравновесные фазовые переходы в системах ферментативных реакций при наличии суб­стратного ингибирования и диффузии. Показана возможность пространственного разделения фаз, соответствующих комплек­сам фермента с несколькими молекулами субстрата. Есть осно­вания думать, что эти же представления окажутся весьма важ­ными для понимания функционирования биологических регуля­торных систем, в частности мембранных.

Как мы уже не раз подчеркивали, имеется далеко идущее сходство между химическими открытыми системами и системами экологическими — соответствие между моделями Лотка и Воль­терра (см. стр. 411). Посмотрим, каким образом аналогия с фа­зовыми переходами проявляется в моделях эволюционирующих популяций [120].

Рассмотрим менделевскую диаллельную популяцию диплоид­ных организмов с полным скрещиванием.

Цр-f v(l — р).

(8.141)

Аллель а отвечает дикому типу, b — мутантному. Можно оп­ределить коэффициенты приспособленности генотипов аа, ab, bb, равные соответственно wі, w2, как удельные скорости роста численности соответствующей популяции

Пусть частота прямых мутаций а —► 6 на поколение равна ц, частота обратных мутаций b —* а равна v. Как показывает дина­мическая теория популяций (ср. [121, 122]), динамика частоты р появления гена а описывается уравнением

(ші — w2) р + ІЩ — виз) р

Шір2 + 2ffi>2p (1 — р) + виз (1 — р):

Здесь время измеряется в числе поколений. При выводе урав­нения (8.141) предполагалось, что [i, v< I; — w2, w2 — w3

(8.142)

W2. В этом случае вид формулы не зависит от того, что чему предшествует, — мутация отбору или наоборот. Перепишем уравнение (8.141) в виде

= R ' (Р) («о ~ aiP — а2р2 — ct3p3),
Где

R (р) = Wlр2 + 2®2р (1 _ р) + о>з (1 - р)2 > 0, (8.143)

/ а0 = vwu al = y, w1 — K, a2 = K(3q—l)/q,

А3 = х(1 — 2q)/q, k = w2 — w3. '

Величина q выражает степень доминирования аллели а в гете - розиготе ab, т. е. 0 < q = (w2 — w3)/(wi — ws) < 1. Выражения коэффициентов осі (см. (8.144)) получаются при условиях {3 w2,

Ц, V 1, V < ц.

В стационарном состоянии популяции р = const, и из (8.142) находим для стационарных значений р

А0 = f (Р) = «іР + а2р2 + а3р3. (8.144а)

Изменению условий существования популяции отвечает из­менение параметров р, ц, v, определяющих, согласно (8.142), темп эволюции и, согласно (8.144а), ее конечный результат. Диа­грамма стационарных состояний — зависимость f от р (8.144а)—■ совершенно подобна зависимости (8.123), представленной рис. 8.45. Эти «ван-дер-ваальсовы» кривые получаются при раз­личных значениях к при условиях к < ци>і (aj > 0) и q < '/з (a2 < 0, a3>0). При этом кубическое уравнение (8.144а) имеет три вещественных положительных корня, совпадающих в критической точке, в которой

И одновременно

ЧцЛр 9(1 — 2q) (1 — 3(/ + 3q2) ' \%)кр Зш,? (1 - 2<?) '

При к > икр существуют три стационарных значения р! < < Рз < р2, причем рз — неустойчиво, а Рь р2 — устойчивы. По­добно реальному газу популяция способна пребывать в двух устойчивых стационарных состояниях, переход из одного состоя­ния в другое аналогичен фазовому переходу первого рода. Пе­реход вызывается достаточно большими флуктуациями числен­ности и состава популяции.

Допустим, что популяция непрерывно расселена в своем ареале. Динамика популяции описывается уравнением, вклю­чающим миграцию особей (диффузию)

4F = iHp) + DV2p, (8.147)

Где г|з(р)—правая часть уравнения (8.142), а коэффициент диф­фузии D выражается через среднее расстояние г, на которое мигрируют особи за время жизни т, D = г2!т. Диффузия не на­рушает устойчивости пространственно однородных стационар­ных состояний, представляемых решениями для нераспределен­ной системы (8.144). Однако при этом возможно появление устойчивого пространственно неоднородного распределения р(л). Могут возникать две пространственно разделенные фазы, каж­дая из которых отвечает устойчивому состоянию. Согласно (8.147) условие их устойчивого сосуществования находится пу­тем минимизации функционала

W=^2?dr, (8.148)

Где лагранжиан 3? {р, Vp) равен

^ = V2D(Vp)2-^(p)dp. (8.149)

Минимизация (8.148) при постоянстве полного объема системы дает

Рг

Ф(Рі) = ЧФ2) = 0, J $(p)dp = 0. (8.150)

P.

Первое равенство (8.150) есть условие стационарности решений pi и р2, второе аналогично условию Максвелла для газа Ван - дер-Ваальса.

Аналогичные соотношения получены ранее Шлёглем для ав­токаталитической реакции (см. стр. 466), дополненной диффу­зией [117].

Пространственное разделение популяции есть первый этап на аллопатрическом пути видообразования. Дальнейшее суще­ствование аллопатрической формы приводит к накоплению в ней новых признаков и к биологической изоляции. Географическое разделение популяции оказывается подобным пространствен­ному разделению при равновесном фазовом переходе первого ряда.

Структура популяции, эволюционирующей согласно уравне­нию (8.141), может претерпевать и переходы, подобные фазовым переходам второго рода, если при некоторых бифуркационных значениях параметров нарушается устойчивость стационарных состояний по отношению к малым флуктуациям. Такой переход происходит при обращении аі в нуль, т. е. при к = {iwi. Ста­ционарная зависимость p(ai) имеет излом в точке ао = 0, ха­рактерный для фазового перехода второго рода— кривые p(ai), т. е. р(—к), совершенно подобны изображенным на рис. 8.47. Величины р, а0 и ai = \vw\ — х аналогичны, соответственно, на­магничению, напряженности магнитного поля и отклонению от точки Кюри (Г — Тк)/Тк для перехода ферромагнетик — пара­магнетик. Можно показать, что вблизи точки перехода резко возрастает время релаксации флуктуаций в устойчивом стацио­нарном состоянии и восприимчивость системы к изменению па­раметров. В распределенной системе, описываемой (8.147), при дополнительном включении в нее случайных внешних воздей­ствий объемные флуктуации и радиус корреляции флуктуаций возрастают с приближением к точке перехода. Переход к новой организации через точку потери устойчивости происходит флук - туационно — все большие объемы захватываются коррелирован­ными флуктуациями, являющимися результатом малых внеш­них воздействий. Популяция приобретает при этом лабильность, которая может привести к быстрой эволюции, например, к вьн ходу в новую адаптационную зону (ароморфоз). Такое «вскрьк тие эволюционных резервов» происходит при низкой интенсивно­сти избирательной элиминации. В эволюции этапы непрерывного развития в устойчивом режиме чередуются с переходными эта­пами, подобными фазовым переходам.

Таким образом, биологическое развитие оказывается связан* ным с нелинейными явлениями типа фазовых переходов. Даль-; нейшее построение соответствующей теории представляется мно^ гообещающим. Проблемы развития рассматриваются в следую^ щей, заключительной главе книги.