ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ИММУНИТЕТ

Специфические процессы клеточной дифференцировки ответ­ственны за иммунитет, в частности, за продукцию антител в ор­ганизмах позвоночных. Имеющаяся сейчас информация об этих процессах позволяет сформулировать физические проблемы, от­носящиеся к иммунитету, и подойти к их решению.

Строение и функции антител (AT) описаны в § 1.3. Природа взаимодействия антител с антигенами (АГ) в основном уста­новлена. Вторая главная проблема иммунологии — проблема возникновения иммунитета — гораздо сложнее.

Хорошо известно, что иммунная система животного служит для борьбы с болезнетворными микроорганизмами. Можно было бы думать, что эволюционное происхождение системы специфи­ческого иммунитета связано с этой жизненно важной задачей. Современные представления об иммунитете приписывают ему более широкую функцию контроля за генетическим постоянством клеток организма. Главной задачей иммунной системы, воз­можно, является устранение мутантных (в частности, раковых) клеток из организма многоклеточного животного. Работа специ­фической иммунной системы выражается в том, что в ответ на появление генетически чужеродного материала (антигена) орга­низм вырабатывает специфические реактивные клетки (клеточ­ный иммунный ответ) и специфические антитела (гуморальный иммунный ответ). Как специфические реактивные клетки, так и антитела могут циркулировать в организме и специфически взаимодействовать с АГ. В результате этого взаимодействия чу­жеродный материал может быть инактивирован, разрушен или фагоцитирован клетками ретикуло-эндотелиальной системы. Со­временные представления об иммунитете основываются на кло- нально-селекционной теории Бернета [146—149]. Этой теории предшествовали качественные идеи, высказанные Ерне [150]. В организме производятся лимфоциты, каждый из которых чув­ствителен к одному АГ или к нескольким родственным АГ. Воз­никают лимфоциты, чувствительные практически к любым АГ, в том числе и к таким, с которыми организм никогда не встре­чается в условиях своего биологического существования. Это оп­ределяется наличием на мембранах лимфоцитов специфических рецепторов, имеющих высокое сродство к определенному анти­гену. Антиген действует как фактор селекции, стимулирующий развитие клонов иммунологически активных клеток из лимфоци­тов, имеющих рецепторы к данному антигену. Таким образом, лимфоцит унипотентен в смысле взаимодействия с АГ. Мы не останавливаемся здесь на генетических факторах, определяю­щих синтез АТ-подобных белков рецепторов (см. [151 —153]).

Наряду с клонально-селекционной теорией следует упомя­нуть о гипотезе матричного действия АГ, предложенной Гау - ровицем [154, 155]. Согласно этой гипотезе, роль АГ состоит в стимуляции определенных генов внутри лимфоцита, который мультипотентен. АГ есть внутриклеточный фактор селекции, AT надолго сохраняются в клетке. Сциллард считал, что син­тез AT подобен индуцированному синтезу ферментов (см. § 1.6), и построил соответствующую модельную теорию [156]. АГ трак­туется в ней как индуктор, снимающий репрессию синтеза спе­цифического у"гл°булина. Однако клонально-селекционная теория лучше обоснована и подтверждена многочисленными фактами.

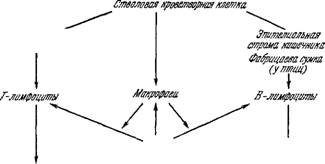
Установлено, что основными продуцентами антител являются зрелые плазматические клетки [149, 151, 152, 157]. Специфич­ность продуцируемых AT совпадает со специфичностью рецеп­торов, находящихся на поверхности клеток-предшественников [157]. Предшественниками плазматических клеток, клетками, воспринимающими антигенный стимул, являются так называе­мые В-клетки, относящиеся к малым лимфоцитам и образую­щиеся в результате дифференцировки стволовых кроветворных клеток. Роль рецепторов в В-клетках играют "иммуноглобулины (104 — 105 молекул на клетку), В-клетки сами по себе не де­лятся, они приобретают способность к пролиферации только после бласт-трансформации, т. е. после превращения в так на­зываемые бласты (у-клетки) под действием АГ [149, 151]. Бласт« трансформация происходит по истечении латентного периода'* длящегося 24—48 часов. г/-клетки интенсивно пролиферируют. Часть у-клеток дает начало клонам плазматических клеток (z-клетки). Данный клон z-клеток вырабатывает антитела, спе^ цифичность которых совпадает со специфичностью рецепторов на поверхности клеток-предшественников [149, 152, 157, 158]. Зрелые z-клетки к дальнейшему делению не способны, они су­ществуют в течение нескольких десятков часов.

Стимулированные антигеном В-лимфоциты могут, наряду с образованием клона плазматических клеток, привести к обра­зованию так называемых клеток иммунной памяти [146, 147, 151, 152]. Если организм отвечает на АГ, воздействию которого он подвергался ранее, то обычно его иммунный ответ оказы* вается более быстрым и сильным. Это явление называется им­мунной памятью. Оно связано с увеличением числа клеток, спо­
собных отвечать на повторный антигенный стимул аналогично первоначальным В-лимфоцитам [157].

Второй популяцией лимфоцитов, способных к специфиче­скому распознаванию генетически чужеродного материала, яв­ляются так называемые Т-клетки. Они, так же как и В-клетки, возникают из стволовых клеток, но в своем развитии обяза­тельно проходят через тимус. Часть 7'-клеток ответственна за клеточные иммунные реакции. В ответ на антигенный стимул

Элитшашая строма тимуса

Еласты (уТ-ттт)

АГ

Т-В-талерация

-шет/ги)

Г-B-mmm памяти \

И /ШМЯИШ • ^

1Г

Зрфеторте югетт тлага омму, (z-штт)

Тегпачша

АГ

Рис. 9.19. Схема событий, вызываемых введением антигена.

Они дифференцируются в специфические реактивные клетки (так называемые киллеры). Две другие подпопуляции Г-кле - ток (хелперы и супрессоры) играют регуляторную роль в раз­витии гуморального (а, возможно, и клеточного) иммунного от­вета. Степень участия регуляторных 7'-клеток в гуморальной иммунной реакции зависит от природы антигена. Существуют так называемые тимус-независимые антигены, способные вызы­вать нормальный ответ без помощи 7'-клеток ([152], см. также [159]).

На рис. 9.19 показана схема описанных событий [152].

Одна из важных задач биофизики состоит в построении физи­ко-математической модели явлений, происходящих при развитии

18 M. В. Волькенштейн

Иммунного ответа. Естественно, что такая модель не должна описывать все детали процесса, еще недостаточно изученные. Модель предназначена для качественного и полуколичествен­ного рассмотрения его важнейших особенностей. Соответствую­щие попытки имеются в литературе. Модель, предложенная в [160], описывает развитие клона АТ-продуцирующих клеток, т. е. ограничивается лишь частью процесса, не рассматривая им-, мунную реакцию в целом. Более сложная модель представлена в работе [161]. Другая модель предложена в работах [162, 163]. Однако она сформулирована в абстрактных терминах, затруд­няющих биологическую интерпретацию. Наиболее разработаны модели Белла [164, 165]. Модели, предложенные в [164], дают детальное описание иммунной реакции, используя весьма кон­кретные предположения о механизмах, которые, к сожалению, в некоторых случаях не установлены достоверно. Расчеты, вы­полняемые на ЭВМ, приведены в согласие с эксперименталь­ными данными по иммунным реакциям у кроликов. В более поздней работе [165] ставится задача построения достаточно простой модели, допускающей качественное исследование. Эта модель получила дальнейшее развитие в работах Пимблея [166]. В перечисленных работах (за исключением [160]) не учитыва­лись прямо эффекты запаз­дывания, связанные с ла­тентными фазами в процес­сах дифференцировки кле­ток.

Изложим здесь основ­ные результаты исследова­ния, проведенного в рабо­тах [167]. Задача состояла в построении модели, опи-г сывающей работу иммунной системы в целом и по­зволяющей с помощью ка­чественного исследования^ предсказать характер течения иммунной реакции в различных^ условиях с тем, чтобы выработать тактику целенаправленного вмешательства в ход иммунной реакции. Модель пока ограничи­вается рассмотрением гуморальной иммунной реакции.

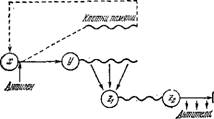
Рис. 9.20. Схема развития АТ-продуци­рующих клеток.

Волнистые линии означают. пролиферацию.

На рис. 9.20 показана используемая схема развития клона АТ-продуцирующих клеток. Как уже отмечалось, плазматиче­ские клетки (z) являются основными продуцентами антител. Развитие плазматических клеток из В-лимфоцитов требует при­близительно 3—4 дня (см., например, [151]). Поэтому иммунный ответ, состоящий в выработке AT, запаздывает по отношению к моменту стимуляции. Формирование клеток иммунной памяти

Требует, по-видимому, еще большего времени. Запаздывание в производстве AT и в формировании иммунной памяти является существенной чертой иммунной реакции.

Во-первых, продолжительность запаздывания не мала по сравнению с характерными временами процесса. Во-вторых, ма­тематическое исследование, проведенное в работах [167], пока­зывает, что продолжительность запаздывания может быть ре­шающей для характера течения иммунной реакции. В указан­ных работах запаздывание учитывается в упрощенной форме сосредоточенного запаздывания.

(9.55)

Скорость выработки антител пропорциональна наличному количеству плазматических клеток, которое определяется чис­лом В-лимфоцитов, стимулированных ранее, в момент времени, отстоящий от текущего на время запаздывания tr. Аналогично, выработка клеток памяти определяется числом актов стимуля­ции В-лимфоцитов в момент, отстоящий от текущего на опре­деленное время запаздывания tm. Процесс описывается следую­щей системой дифференциальных уравнений с запаздывающим аргументом:

X = J — x~lx(t) — Рх (t)g (t) + Атх (t - tm) g(t - tm) Є (t - tm),

G = Kg(t)-Qh(t)g(t),

H = Arx ({ - tr) g{t - tr) 0 (i - tr) - Rh {t) g (t) - Sh (0.

Здесь x, g, h — соответственно количества В-лимфоцитов, анти­гена и антител;

Если t < 0, если t ^ 0,

(9.56)

/ — скорость пополнения популяции 5-лимфоцитов в результате дифференцировки стволовых клеток, т — среднее время жизни 5-лимфоцитов. Члены —Px(t)g (t) и Атх (t — tm)g (t — tm)Q (t — tm) описывают соответственно уменьшение популяции В-лимфоци­тов в результате контакта с АГ и ее пополнение вследствие фор­мирования клеток иммунной памяти. Клетки памяти считаются идентичными первоначальным В-лимфоцитам, К характеризует скорость репродукции АГ в условиях организма (К < 0 в слу­чае неразмножающегося АГ). Члены —Qh(t) g(t) и —Rh(t)g(t) описывают соответственно уменьшение количеств АГ и AT в ре­зультате их взаимодействия. Член Arx(t — tr)g(t — tr)Q(t — tr) описывает производство AT, S характеризует скорость рас­пада AT.

Параметры Р, Ат, Ar, tr, tm, которые в дальнейшем считаются постоянными, в действительности могут зависеть от динамики численности регуляторных Г-клеток. Такое упрощение корректно при описании иммунного ответа на тимус-независимый АГ или

IS*
При быстром достижении стационарного уровня количества Ре­Гуляторних клеток. Рассмотрение системы (9.55) с постоянными параметрами необходимо также как первый шаг в изучении по­ведения полной системы, учитывающей динамику регуляторных клеток.

Уравнения (9.55) описывают систему специфического гумо­рального иммунитета. Здесь не учитывается спонтанный синтез антител и не рассматривается в явном виде действие неспецифи­ческих факторов защиты организма. Отметим только, что ука­занные механизмы, по-видимому, создают первый барьер для инфекции.

Уравнения (9.55) позволяют при разумных значениях пара­метров правильно описать динамику иммунного ответа на вве­дение неразмножающегося (К < 0) АГ. Однако наиболее инте­ресным представляется изучение иммунной реакции в случае размножающегося АГ. Далее, не приводя математических вы­кладок, мы опишем характерные особенности решений системы (9.55) при К > 0. Если

(.IxArQ/KR)1/г - 1 < (Sx (Р - Am)/R)'!\ (9.57)

Что соответствует большой скорости расходования В-лимфоци- тов, система (9.55) имеет единственное стационарное решение

Х0 = Jx, g0 = 0, fto = 0. (9.58)

Такое стационарное состояние без антигена и специфических антител неустойчиво. Если выполнено условие (9.57), то при по­падании размножающегося АГ в организм, его количество на­растает неограниченно.

Если неравенство (9.57) нарушено и

Р > Ат, (9.59)

То, помимо неустойчивого стационарного состояния (9.58), си­стема (9.55) имеет следующие стационарные решения:

2Arq • і

(9.60)

KR

Xi = [JxArQ/KR + 1 - (Р - Ат) Sx/R + DV2] ■ gl = [JxArQ/KR - 1 -(P-Am) Sx/R - Dv°] -2 (p _ Am)- , h = K/Q

V,1 KR

*2 = [JxArQ/KR +\-(P-Am) Sx/R - DVl]

2ArQ '

(9.61)

2{P-Am)x '

G2 = [JxArQ/KR - 1 - (P - AJ Sx/R + D"2] h2=KjQ,

Здесь

D = [JxArQ/KR + 1 ~(Р~Ат) Sx/RY - 4JxArQ/KR.

Стационарные точки (9.60), (9.61) слиты в одну, если (JxArQ/KR)'!* — l=[(P — Am)Sx/R],'h и различны (*, > g, < <g2), если выполняется неравенство, обратное (9.57). Если (Р — Ат) стремится к нулю, то Xi-*Jx, gi —*S/[R(JxArQ/KR—1)] и Х2 KR/AQ, Как показало исследование стандарт­

Ными методами, стационарная точка (9.61), соответствующая большему количеству АГ, неустойчива. Характер стационарной

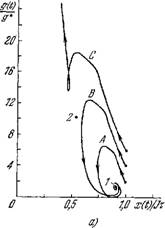
Рис. 9.21. Проекции фазовых траекторий системы (9.55) на плоскость

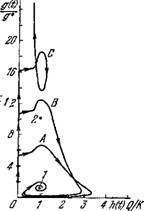
(х, g) (а) и \h, g) (б). Траектории построены для < ЛС = 1; х (0) = /т; ft (0) = 0; fxArQ/KR = 2\ ТЛГ=2; PS/RKГ = 0,04; Ат = 0; SIK = 3 и различных начальных количеств антигена g (0)/g*, равных 2 (Л), 4 (В) и 6 (С). g*=s/[R (harqikr— 1)] 1 н 2—стационарные точки.

Точки (9.60) зависит от продолжительности запаздываний. Она устойчива прн малых запаздываниях. В этом случае в зависимо­сти от начального количества АГ возможно: а) стремление ре­шений системы к стационарному состоянию (9.60); такое реше­ние указывает на возможность длительного сосуществования инфекции со специфическими антителами (состояние носитель- ства); б) неограниченный рост количества АГ (рис. 9.21). По мере увеличения запаздываний уменьшается минимальное на­чальное количество АГ g(0), приводящее к неограниченному размножению АГ. Кроме того, стационарная точка (9.60) ста­новится неустойчивой. Поэтому при малых начальных количе­ствах АГ возможно возникновение предельного цикла — перио­
дическое течение болезни (рис. 9.22). При достаточно большом запаздывании в формировании иммунного ответа (tr) количе­ство АГ растет неограниченно, независимо от начальных

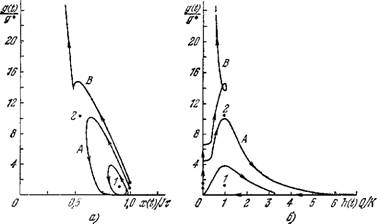
Рис. 9.22. Проекции фазовых траекторий системы (9.55) на плоскость (х, g) (а)

И (A. g) (б).

Траектории построены для < К=1,5 и g (0)/g* = l (кривые A), g(0)/g* = l,5 (кривые В). Значения остальных параметров и начальные данные те же. что и для рис. 9.21.

Условий. При Р > Ат условие, обеспечивающее неограниченный рост количества АГ, имеет вид

/Т Ktr ехр (- Юг) < ехр (- 1), Ktr> 1 • (9.62)

Рассмотрим теперь ситуацию, когда интенсивность формирова­ния клеток памяти больше интенсивности расходования В-лим - фоцитов в результате контакта с АГ, т. е.

Ат > Р. (9.63)

В этом случае система (9.55) обладает единственной поло­жительной стационарной точкой (9.60). Необходимое и доста­точное условие устойчивости этой стационарной точки при tr = = tm = 0 имеет вид

В силу (9.64) при tr = tm — 0 стационарная точка (9.60) (Ат > Р) устойчива, в частности при St > 1 (так как Х\ > > KR/AQ).

Если стационарная точка (9.60) (Ат > Р) устойчива при нулевых запаздываниях, она устойчива и при достаточно малых запаздываниях. Увеличение запаздываний неизбежно приводит к неустойчивости стационарного состояния. Для малого запаз­дывания в формировании иммунной памяти, такого, что

Атехр(-Ют)>Р, (9.65)

Решения системы (9.55) ограничены. Следовательно, если (9.65) выполнено, то возможны два типа решений.

А) Стремление к стационарному состоянию — стационарная точка (9.60) (Ат > Р) устойчива; б) циклические решения — стационарная точка (9.60) (Ат > Р) неустойчива. Если tm столь велико, что условие (9.65) нарушено, то можно показать, что для любых tr достаточно большие начальные количества АГ ведут к неограниченному росту его количества. Более того, для достаточно больших значений tr количество АГ растет неогра­ниченно при любых исходных количествах АГ.

Для более детального изучения зависимости течения иммун­ной реакции от значений параметров удобно вместо (9.55) рас­смотреть более простые уравнения. Вырабатываемые системой АТ имеют высокое сродство к АГ. Поэтому до тех пор, пока ко­личество АГ не слишком мало, появляющиеся АТ быстро реаги­руют с АГ. Действительно, заметные количества АТ наблю­даются лишь после удаления АГ [168]. Это обстоятельство по­зволяет аппроксимировать систему (9.55) уравнениями

X = 7 - т-1* (t) - Рх (t) g (t) + Атх (t - tm) g(t - tm) Q(t — tm), g = Kg{t)-Ar-Q-x(t - tr) g(t — tr) Q{t - tr).

(9.66)

Уравнения (9.66) описывают «борьбу» между В-лимфоцитами и антигеном, причем быстро действующий медиатор — антитела — не представлен в них явно. Уравнения (9.66) сходны с уравне­ниями Вольтерра для системы «хищник — жертва» (см. § 8.3), если Ат > Р. Отличие от уравнений Вольтерра состоит в нали­чии запаздывания в нелинейных членах. В нашем случае АГ играет роль «жертвы». Замена уравнений (9.55) уравнениями (9.66) формально соответствует бесконечной скорости взаимо­действия АТ с АГ. Это значит, что уравнения (9.66) не выпол­няются при g(t), близких к нулю.

Однако расчеты показывают, что уравнения (9.66) правильно описывают характерные черты иммунной реакции. Обращение g(t) в нуль, согласно уравнениям (9.66), соответствует большой вероятности уничтожения АГ в реальном процессе. Особенности течения иммунной реакции, связанные с конечной скоростью взаимодействия АГ с АТ, рассмотрены подробно в [167].

В рамках системы (9.66) найдены условия уничтожения АГ или неограниченного роста его количества.

Эти условия, в частности, показывают роль запаздываний в развитии иммунной реакции. Так, для эффективной супрессии быстро размножающегося АГ запаздывание в развитии иммун­ного ответа tr должно быть не слишком малым и не слишком большим.

Уравнения (9.66) имеют ненулевую стационарную точку

Хо = к/лг> g0 = (t — ArJx/K)/[Am х (1 - P/Am)l (9.67)

Физический смысл имеют лишь значения go > 0. Устойчивость этой точки исследуется обычным методом линеаризации урав­нений (см. стр. 397). Переходя к безразмерным переменным | = х/хо, г] — g/go, получаем вместо (9.66) уравнения

К~ л = Ті (0 - l(t - tr) ті (t - tr) Є {t - tr), j

Xi = a-l{t)-bl (t) т| (0 + c| {t - tm) n (t-tm) 9 (t-tm), )

(9.68)

Где a = JxAr/K, b =(l — а)Р/ (Am — P), с = bAJ{Am — P), a, b,c — положительны и связаны условием а — b + с= 1. Ста­ционарная точка имеет координаты г) = 1, 1. Характеристиче­ские числа Я являются корнями квазиполинома

(1 - К/К)(1 + й + Ят)-(1 +Ят) ехр (— Ur) —

- с (1 - УК) ехр (- Мп) = 0. (9.69)

При нулевом запаздывании (tr = tm = 0) и а > 0 оба корня имеют отрицательные вещественные части и точка асимптоти­чески устойчива. Если Q = 0, то оба корня чисто мнимые. Если а > 0, то стабильность сохраняется для достаточно малых не­нулевых tr, tm. Их возрастание нарушает устойчивость. При а = 0 любые отличные от нуля значения U и tm приводят к не­устойчивости. Если а = b = 0, то уравнения (9.68) принимают вид

Эти уравнения отличаются от уравнений Вольтерра — Лотка только наличием запаздываний в нелинейных членах. Колеба­тельный характер системы, сохраняющийся и при ненулевых значениях tr и tm, проявляется в циклической кинетике иммун­ной реакции.

На рис. 9.23 показаны примеры решений уравнений (9.70). Можно было бы ожидать, что увеличение запаздывания в фор­мировании иммунной памяти tm должно всегда приводить к уве­
личению времени, требуемого для элиминации АГ. В действи­тельности, однако, нарастание неустойчивости с ростом запаз­дывания может привести к сокращению времени реакции бла­годаря уменьшению числа обходов стационарной точки (см. рис. 9.23).

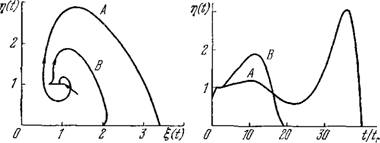
Рис. 9.23. Решения уравнений (9.70) в безразмерных единицах при trK = trx~l = = 0,3; |(0) = 1,4; ті (0) = 0,75 и для tm, равных 1,5\tr (Л) или 2,5 tr (В).

Учтем теперь конечную скорость реакции АТ и АГ, считая, что количество В-лимфоцитов мало меняется в ходе иммунной реакции, т. е. х(/)?»х(0). Уравнения (9.55) принимают форму

G = W)-Qh{t)g(t), j

H = Ag(t - tr) 9(t - tr) - Rg(t) hit) - Sh(t), ) где A = Arx(0). Если

KR/AQ < 1,

(9.71)

(9.72)

Система (9.71) имеет две стационарные точки (0,0) и

(9.73)

Стационарная точка (0, 0) неустойчива, характер стационарной точки (9.73) зависит от параметров и, в частности, от запазды­вания tr. Кривая, разделяющая области устойчивости и неустой­чивости стационарной точки в плоскости (trK, trS), задается па­раметрически следующим образом:

TrK-

У. о — П - KR/AQ) у sin у

Cos у — KR/AQ '

(9.74)

Sin у

0<*/<Arccos (KR/AQ).

В частности, стационарная точка (9.73) устойчива при trK < 1 и неустойчива при trK> я/2 (для любого KR/AQ < 1).

Система (9.71) не допускает неограниченного роста количе­ства антител (h(t)). Количество АГ растет неограниченно при выполнении1 одного из следующих условий:

> 1

AQ

(9.76)

KR

(9.75)

Или

AQ

JrfctrKexp(-Ktr)<l и Ktr> 1.

Е(,ли (9.75) и одно из неравенств (9.76) нарушено, то количе­ство АГ ограничено.

M, L 3

Итак, при выполнении условия (9.75), когда система (9.71) обладает только нулевой стационарной точкой, количество АГ неограниченно нарастает. В условиях (9.72), когда система об­ладает двумя стационарными точками, пространство параметров

1L 2 М 3 trK О Q2 0,40,50,6 0,8 1,0 КК/АО А) 'Б;

Рис. 9.24. Разбиение плоскости параметров (trK, trS) на области, соответ­ствующие различным режимам системы (9.71) (Л), и значения характерных точек L и М разбиения в зависимости от KR/AQ (Б). Точки а, б, в, г, д соответствуют фазовым траекториям, приведенным на рис. 9.25.

(trK, trS, KR/AQ) распадается на области, соответствующие раз­личным режимам реакции. На рис. 9.24, Л показано разбиение плоскости параметров (trK, trS) при KR/AQ = 0,5. В области / стационарная точка (9.73) устойчива, количество АГ ограни­чено; в области // стационарная точка (9.73) неустойчива, ко­личество АГ неограниченно нарастает.

Разбиение выполнено на основе условий (9.74) и (9.76). Видно, что с увеличением запаздывания tT система переходит из области / в // и далее в ///. На рис. 9.24, Б приведены значения L и М (см. рис. 9.24, А) в зависимости от KR/AQ:

L = Arc cos (KR/AQ)/[ 1 - (KR/AQ)2]'1', Ме~м = , M> 1.

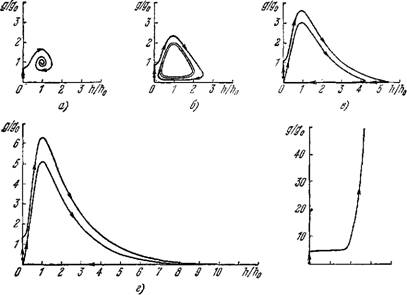
На рис. 9.25 приведены примеры фазовых траекторий системы (9.71), полученные с помощью ЭВМ. Соответствующие значе­ния параметров обозначены на рис. 9.24, А крестиками. Рис. 9.24, А (область /, устойчивая стационарная точка) соот­ветствует такому течению болезни, когда, начиная с некоторого

О 0,05 0,1 Ь/!)в 3)

Рис. 9.25. Фазовые траектории системы (9.71) в безразмерных переменных g/go, h/h0 (см. (9.73)) для KR/AQ = 0,5; S/K = 3 и значений запаздыва - ' ния trK, равных I (я), 1,25 (б), 1,5 (в), 1,75 (г) и 3 (д).

Момента, болезнь не прогрессирует, а количество АГ в орга­низме практически постоянно (организм становится носителем инфекции). Если

S KR /(. KR \

Достаточно мало, то стремление решений системы к стационар­ному состоянию соответствует, по-видимому, выздоровлению. В области // (см. рис. 9.24, Л) система имеет предельный цикл (см. рис. 9.25,6 — г), что соответствует периодическому течению болезни. С увеличением запаздывания амплитуда колебаний увеличивается, а минимальное количество АГ уменьшается. При этом доля времени, в течение которого количество АГ близко к нулю, растет (0,5 от продолжительности цикла в случае в и

0,7 — в случае г). Минимальные количества АГ для случаев в, г равны соответственно 8- Ю-4 и 8- Ю-10 от стационарного.

При учете конечной скорости реакции АГ с АТ в рамках де­терминистических уравнений (9.55), (9.71) полная элиминация размножающегося АГ невозможна. В действительности, если со­гласно детерминистическим уравнениям достигаются малые ко­личества АГ, то должен проявиться дискретный стохастический характер процесса размножения и гибели микроорганизмов, что делает возможным полное уничтожение АГ. Циклический ха­рактер решений согласно детерминистическим уравнениям ука­зывает на возможность рецидивов в ходе заболевания. В [167] предложен метод для оценки вероятности уничтожения А Г. На основе этого метода был исследован вопрос об оптимальной так­тике лечения с точки зрения предотвращения рецидивов. Пока­зано, что наиболее целесообразно вводить специфические АТ (сыворотку) в момент максимального количества собственных АТ. При использовании антибиотиков наибольший эффект достигает­ся, если начинать их применение в тот момент, когда количество АГ максимально. Слишком раннее применение как антибиоти­ков, так и антител ослабляет собственный иммунный ответ орга­низма, что приводит к увеличению вероятности рецидива. Мо-, дель также показывает, что в случае слабых хронических ин­фекций одним из приемов лечения может быть преднамеренный перевод заболеваний в острую форму, что позволяет активизи­ровать иммунный ответ организма и тем самым увеличить ве­роятность полной элиминации АГ.

Проблемы возникновения иммунитета — проблемы развития. Можно думать, что принципы трактовки иммунитета, такие, как учет запаздывания, а также рассмотрение фазовых переходов щ неравновесных мультистационарных системах (см. § 8.1,2) по| могут математическому моделированию процессов развития — онтогенеза, канцерогенеза, биологической эволюции.

[1] (р, т)=c;'eqc2\... (2.7)

[2] В тех случаях, когда это не может привести к недоразумениям, сами реагенты и их концентрации обозначаются одинаково.

[3] Здесь и далее сами частицы мы также будем обозначать через А, В и т. д.

[4]

При которых два экстремума х

X'-

Рис. 8.31.

Ингибированием.

Гиба, для которой dx/dv — 0. Если такая нелинейность имеет место, то возникает ряд специфических явлений, в частности, множественные стационарные состояния, их неустойчивость, ги - стерезисный характер зависимости v от параметров системы и