ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ БИОЛОГИЧЕСКОЙ ЭВОЛЮЦИИ И ЦЕННОСТЬ ИНФОРМАЦИИ

Модельная теория Куна, изложенная в предыдущем пара­графе, естественно, не претендует на то, чтобы реконструиро­вать истинный путь эволюции на Земле. Как пишет Кун, задача теории состоит в том, чтобы «описать модель, эксперименталь­ная проверка которой позволяет лучше познать принципы, важ­ные для эволюции» [55]. Эта модель основана на действительно важных принципах. Первый принцип — необходимая реализа­ция маловероятных событий в больших популяциях, размножаю­щихся в открытой системе, далекой от равновесия. Второй прин­цип — определяющее значение ценности информации при воз­никновении вторичной и третичной структуры, агрегации и т. д. Третий принцип — организующее значение периодичности, на­личие чередующихся стадий синтеза и распада, определяемых сменой дня и ночи. Последний принцип впервые введен в рас­смотрение в работе Куна.

Остановимся на втором принципе. Ценность информации, со­держащейся в макромолекуле в соответствии с теорией Эйгена, можно представить селективной ценностью, выражаемой через кинетические параметры. Для осуществления эволюции кинети­ческие процессы должны быть автокаталитическими и, тем са­мым, нелинейными. Здесь важно положение, отмеченное на стр. 494: автокатализ должен определяться узнаванием доста­точно протяженной системы мономерных звеньев, а не отдель­ных звеньев. Только при этом условии селективная ценность об­ретает смысл ценности информации, заложенной в макромоле - кулярной цепи.

Ценность информации впервые появляется в модели Куна при рассмотрении селекции D - или L-рибозы, необходимой для образования стереоспецифической цепи пра-тРНК, обладающей определенной вторичной структурой. Тем самым, возникновение хиральности считается очень ранним событием. В принципе по­явление хиральности можно отнести и к более поздней стадии. Преимущество хиральности для структурирования РНК оче­видно, однако необходимо объяснить, каким образом хираль - ность может быть зафиксирована. Вообще говоря, возможно од­новременное образование двух энантиомерных популяций, одна из которых состоит из D-звеньев, а другая — из L-звеньев. В це­лом система рацемична, подобно, например, месторождению кристаллического кварца, в котором встречаются с равной ве­роятностью правые и левые кристаллы. Однако при случайном, флуктуационном превышении численности одной развивающейся популяции над другой возможно эволюционное предпочтение первой популяции и ее преимущественное развитие (ср. [33]). Приведем иллюстративные расчеты.

Пусть xi и х2 — числа молекул пра-РНК в системе, построен­ных соответственно из D - и L-мономеров, обозначаемых mi и т2 Скорости образования х\ из т\ и х2 из т2 одинаковы, одина­ковы и скорости их распада. Кинетические уравнения, описы­вающие развитие системы, имеют вид

Х\ ~ %X[Wi — %Х\,

(9.38)

Х2 — %x2w2 — Хх2,

Где % и X — константы скоростей полимеризации и распада со­ответственно, а

Т, + т2 ' ""2 /П] + т2

— вероятности встречи матриц 1 и 2 соответственно с мономе­рами mi и т2. При любых значениях mi и т2

Xix2 = Xi (0) х2 (0) ехр [(% — 2Х) /]. (9.39)

Система стационарна лишь при х = 2Х. Условию стационарности отвечает рацемат, W\ = w2 = 0,5, т. е. rri\ = т2.

Если концентрация мономеров поддерживается постоянной и свободные мономеры содержатся в большом избытке, то не­тривиальное развитие системы возможно при х > 2% и неравен­стве mi Ф т2 в результате флуктуации. Допустим, без ограни­чения общности, что

И)і = 0,5 + а, да2 —0,5 — а,

Где а = const. Тогда из (9.38) получаем

Х\ = Х\ (0) ехр [(х/2 — X) /] ехр хсс/,

Х2 = х2 (0) ехр [(х/2 — X) і] ехр (— %at) ) (9,40^

С течением времени популяция Xi станет доминирующей:

Ехр 2ха/.

Х, х, (0)

*2 х2(0)

Если мономеры поступают в открытую систему в количе­ствах, пропорциональных их расходованию при полимеризации, т. е. mi и т2 пропорциональны соответственно х\ и х2, то урав­нения (9.38) приобретают нелинейную форму

Х\ = X : ХХ\,

(9.41)

1 X, + *2 ''

—54 v a. v Хх2,

(х-Х)/]},|

Х\ х2

Аналогичные уравнения написаны Аджено [60] для модели, в которой хиральность фиксируется уже на биологической ста­дии в результате полового размножения и генетического об­мена. Решение системы (9.41) имеет вид [60]

= і/2 {[А2 ехр [2 (х - X) t]+4B ехр [(х - 2Х) t]]'1' + А ехр [(> х2 = '/2 {[А2 ехр [2 (х - X) t]+4B ехр [(х - 2Х) t])'k —А ехр [(>

(9.42)

Где А = х,(0) — х2(0), В = *i(0)x2(0). Условие (9.39), конечно, соблюдается. Если хх (0) > х2(0), т. е. А > 0, то при Х<%<2Х с течением времени х\ -* оо, х2 —* 0, при 2Х < х Х\ —► оо, х2 —і► оо, но xjx2 -* оо. При х < X хх —*■ 0, х2 -* 0.

Мы видим, что вопреки утверждениям работы [60] отбор энантиомеров в принципе возможен и на добиологической стадии.

Другая модель, предложенная Франком [61] и Зеелигом [62], исходит из антагонистичности взаимодействий — встреча D - и L-цепей означает их гибель, неспособность к дальнейшему раз­множению. Нелинейные уравнения в этом случае имеют вид

Х\ = KXi — ХХ[Х2) Х2 === УСХ2 — КХ\Х2.

Условия х\ = х2 = 0 дают стационарные значения = = Это неустойчивое решение типа седловой точки на плоскости Х\, х2 (см. стр. 401). В зависимости от начальных условий будет нарастать содержание х1 или х2 и, соответственно, падать содер­жание Х2 или Х\.

Как уже указывалось на стр. 509, уравнения типа (9.43) ис­пользуются в теории происхождения жизни, предложенной в ра­ботах [59] для объяснения селекции первичного кода, и при рассмотрении последующих этапов эволюции.

Проведенное здесь рассмотрение проблемы хиральности по­лезно для понимания информационных аспектов эволюции. Хи - ральность дает количество информации, равное одному биту на звено, т. е. N бит в цепи из N звеньев. Однако суть дела заклю­чается не в количестве информации, а в ее ценности для разви­тия, находящей свое выражение в иллюстративных уравнениях (9.40) или (9.42). Во всех этих моделях ценность хиральности предполагалась абсолютной в том смысле, что размножаются лишь цепи, построенные из звеньев одинаковой хиральности. Можно представить себе иную ситуацию, в которой размно­жаются цепи с разным содержанием D - и L-звеньев, но пол­ностью хиральные цепи обладают максимальной селективной ценностью. В этом случае применима теория Эйгена, модифици­рованная таким образом, чтобы учесть ценность информации, необходимой для формирования третичной структуры цепи.

Значение ценности информации при образовании вторичной и третичной структуры РНК проявляется не только в молекулах тРНК - В работе Шпигельмана по эволюции Qp-PHK in vitro (см. стр. 497) были изолированы реплицирующиеся молекулы РНК, содержащие 218 нуклеотидов [63]. Удалось определить полную последовательность звеньев как в основной цепи этой РНК, так и в ее реплике (комплементарной цепи), и прийти к определенным представлениям о вторичной структуре [64].

(9.43)

Надо отметить, что качественные представления, близкие к идеям Эйгена и Куна, были выдвинуты независимо в работе Шноля [65]. Шноль определяет кинетическое совершенство био­логической эволюционирующей системы как меру эффективно­сти использования свободной энергии для синтеза объектов эво­люции, как меру скорости синтеза, степени изменчивости и
устойчивости и совершенства воспроизведения вариантов струк­туры, возникающих в результате флуктуаций. Эти слова не со­держат физических определений, но Шноль справедливо исходит из доминирующей роли кинетических, а не термодинамических закономерностей в эволюции. Правда, в дальнейшем изложе­нии Шноль отходит от этого принципа и пытается трактовать матричный синтез биополимеров на термодинамической, а не на кинетической основе: «процесс соединения мономеров в цепь должен быть эндергоническим, поскольку, будь этот процесс экзергоническим, способность к самопроизвольному соединению мономеров приводила бы к чрезмерно частым ошибкам в по­рядке чередования мономерных звеньев в полимерной цепи». Это утверждение более чем спорно, оно не учитывает ни кине­тики процесса, ни особенностей его протекания в открытой си­стеме.

Шноль вводит в рассмотрение понятие предельно совершен­ной системы. На добиологическом этапе предельное совершен­ство означает максимальную возможную скорость преобразо­вания веществ окружающей среды в синтезируемые цепи. Мат­рица действует как предельно совершенный катализатор, на­правляющий процесс по уникальному маршруту реакции и обес­печивающий его максимальную скорость.

По существу, количественное выражение сходных представ­лений дано в изложенных выше теориях, надо думать, не един­ственно возможных.

Проведем общее рассмотрение информационных аспектов эволюции. Следуя за Шмальгаузеном [66—68], определим ос­новные понятия, которыми оперирует теория биологической эво­люции.

Материальной основой биологической эволюции являются наследственность и мутационная изменчивость. Регулирующий механизм эволюции — естественный отбор, определяемый, со­гласно Дарвину, взаимодействием организма с внешней средой. Действие этого механизма состоит в борьбе за существование, приводящей к отбору наиболее приспособленных особей. Внеш­ней средой, регулятором, является биогеоценоз [3]. Наименьшей эволюционирующей системой является популяция особей, при­надлежащих к данному виду. Популяция есть объект, управляе­мый регулятором — биогеоценозом.

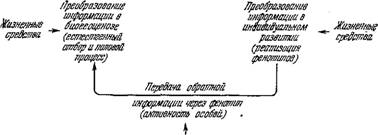
Шмальгаузен предложил кибернетическую трактовку этих регуляторных взаимоотношений [66, 67]. Биогеоценоз получает «информацию» о состоянии популяции посредством неких «об­ратных связей» и, тем самым, «включает в себя специфический механизм преобразования этой информации в управляющие сиг­налы и средства передачи последних на популяцию» [67]. Соот­ветствующая схема показана на рис. 9.7.

Наследственная информация передается от предыдущего по­коления к последующему только после ее преобразования в биогеоценозе. Сама популяция является неотъемлемой частью биогеоценоза. Механизм наследственной передачи содержится в отдельных особях, а изменения биогеоценоза относятся к по­пуляции в целом. Информация об этих изменениях передается через размножение отбираемых особей, потомство которых вли­вается в ту же популяцию. Популяция меняется, эволюциони­рует, но информация об этом изменении передается через раз­множение особей.

Помехи. ♦

Передача. наелеВшеенной

( информации через зиготу 1 и плеточные деления 1

Помехи

Рис. 9.7. Общая схема регулирующего механизма эволюции по Шмальгаузену.

Термин «информация» употребляется здесь не в количествен­ном смысле, и концепция Шмальгаузена имеет чисто биологиче­ский, но не физический характер. Шмальгаузен подчеркивал, что для эволюции существенно не количество информации, со­держащееся в хромосоме, клетке, особи, популяции, но качество, или ценность, информации. «Во всех случаях, когда проводится сравнение и отбор информации, это происходит на основе их оценки по качеству... В биологии основное значение приобретает качественная оценка информации» [66].

Эти положения согласуются с физической теорией эволюции, исходящей из понятия ценности информации (селективная цен­ность по Эйгену). Попытаемся дать характеристику ценности (качества, содержания) информации (см. стр. 94, 510) [91].

Ценность информации, содержащейся в каком-либо сообще­нии, определяется результатами рецепции этого сообщения не­которой системой [91, 92]. Тем самым, ценность должна опреде­ляться применительно к рецепторной системе, к процессу, в ней программируемому. Соответственно информация имеет ценность лишь в неравновесных условиях — в равновесии рецепции ин­формации нет. Рецепторная система является открытой по от­ношению к поступающей информации. Рецепция информации означает переход рецепторной системы из неустойчивого в одно из устойчивых состояний (которое может быть и равновесным). Таким образом, ценность информации определяется неравновес­ностью и неустойчивостью рецепторной системы.

В результате внесения в цитоплазму информационной моле­кулы мРНК синтезируется белковая цепь. Система неустойчива и обладает громадным числом устойчивых состояний — в зави­симости от внесенной мРНК в системе будет транслироваться тот или иной «текст». Если цепь мРНК содержит N нуклеоти­дов, то количество информации в ней на уровне «текста» равно Iog2 = 2N бит. На том же уровне синтезируемая белковая цепь содержит информацию, равную log2 20w3 = 1,44 N бит. Уменьшение количества информации при рецепции определяется вырождением кода. На данном уровне рецепции совместно вы­рожденные кодоны считаются тождественными. Как мы увидим, на другом уровне рассмотрения, учитывающем последствия му­таций, это уже не так (см. § 9.8).

Далее «текст» первичной структуры белка транслируется в пространственную функциональную структуру. При этом ами­нокислотные остатки, близкие по гидрофобности (см. [7], § 4.6), оказываются взаимозаменяемыми. На этом уровне рецепции про­исходит дальнейшее уменьшение количества информации. Вслед­ствие взаимозаменяемости близких по функции белков (напри­мер, протеаз) ее количество уменьшается еще сильнее на уровне рассмотрения функциональности белка.

Ценность на одном уровне отличается от ценности на другом уровне. Яркий пример такой же свертки информации дает язык. При переходе от информации, записанной буквами (безотноси­тельно к природе и смыслу текста), к информации, учитываю­щей корреляции между буквами и словами, и, наконец, к осмыс­ленному тексту все большая часть информации оказывается из­быточной (см. [93], гл. IV).

Таким образом, уровень рецепции является важнейшей ха­рактеристикой ценности информации. Именно неизбыточная ин­формация имеет ценность на данном уровне рецепции, и, сле­довательно, мерой ценности может служить количество неизйы - точной информации. Закон сохранения, связывающий энтропию и информацию

I + S = Const = / max = Smax.

Справедлив лишь при условии, что / и S определяются на одном и том же уровне. Смысл этого закона состоит в том, что энтро­пия означает информацию, которой не хватает для полного опи­сания системы. При возрастании I убывает S и наоборот (см., например, [69, 94]). Величины / и S имеют здесь макроскопиче­ский смысл. Так, при испарении жидкости исчезает макроско­пическая информация о местонахождении молекул в определен­ной части фазового пространства. Соответственно возрастает S. Макроскопическая информация превращается в микроскопиче­скую информацию, например, в информацию о корреляциях ме­жду скоростями молекул в газе, возникающих при их соударе­ниях. Но это уже не информация — ее нельзя ни зарегистриро­вать, ни «запомнить» вследствие неустойчивостей, определяемых соударениями, которые и рождают энтропию (см. стр. 86).

Фазовое пространство системы содержит устойчивые и не­устойчивые области. Через последние проходят сепаратрисы. Устойчивым областям отвечает информация, неустойчивым — энтропия. Для макроскопических систем при достаточно высо­кой температуре фазовый объем неустойчивых областей значи­тельно больше, чем устойчивых.

Возникновение информации (в отличие от трансляции полу­ченной информации) определяется возможностью выбора пути перехода из неустойчивого состояния в одно из нескольких устойчивых. Система, творящая информацию, должна обладать множественными стационарными состояниями (см. стр. 492). Это — диссипативная система, в которой малые флуктуации возрастают до макроскопического уровня. Такими системами яв­ляются и Вселенная в целом, и Солнечная система, и Земля, и биосфера, и человек в своей творческой деятельности.

Рецепция информации может происходить двумя путями. Во- первых, как в приведенном примере с мРНК, рецепторная си­стема может приобретать и перекодировать, транслировать, ин­формацию. Во-вторых, малое количество информации, воздей­ствующей на триггерную систему, может индуцировать создание новой информации. Оба процесса необратимы, в обоих случаях рецепторная система неравновесна и неустойчива. Но аналити­ческое рассмотрение ценности информации возможно лишь в первом случае [95].

Финализм в биологии (см. [7], § 1.2) исходит из рассмотре­ния цели — готовности системы к восприятию информации, т. е. к переходу в устойчивое состояние путем трансляции поступив­шей информации. Наличие цели означает неустойчивость. Сво­бода воли, свойственная высшим животным и человеку, означает возможность выбора пути к одному из многих устойчивых со­стояний. Любой вид творчества есть результат выбора [91, 92, 96].

Утверждение Шредингера о том, что организм есть аперио­дический кристалл, — не только констатация конденсированного состояния и апериодичности. Апериодическая система содержит значительно большее количество ценной неизбыточной инфор­мации, чем эквивалентная периодическая система. Весь аперио­дический кристалл является одной «элементарной ячейкой».

Итак, ценность информации определяется неравновесностью и неустойчивостью рецепторной системы и уровнем рецепции, причем ценна лишь неизбыточная информация. Рецепция ин­формации есть необратимый процесс. Можно определить коли­чественно ценность информации как повышение вероятности до­стижения некоторой цели в результате получения сообщения ([96], см. также [97, 98]).

Восприятие художественного произведения, т. е. текста, од­номерного во времени (литература, музыка), двумерного или трехмерного в пространстве (соответственно живопись и скульп­тура), означает рецепцию ценной информации, программирую­щей эмоции и мысли рецептора [92]. Неустойчивость здесь вы­ражается в готовности к восприятию текста, уровень рецепции связан с «тезаурусом», т. е. с запасом предварительной инфор­мации у рецептора. Сложность проблемы состоит в том, что вос­приятие художественного произведения содержит оба элемен­та — и трансляцию получаемой информации, и создание новой информации в ходе ассоциативных процессов (эмоциональных и интеллектуальных). Последнее именуется сотворчеством.

Опираясь на понятие свертки информации путем отсева из­быточной информации, можно считать, что ценность информа­ции, содержащейся в элементе какого-либо сообщения, тем больше, чем больше последствия замены данного элемента для рецепторной системы. В этом смысле ценность слова в научном тексте значительно ниже, чем в тексте художественном. Одно и то же научное положение можно выразить многими способами без изменения его содержания. Напротив, замена слова в стихо­творении даже синонимом резко изменяет структуру стиха [92]. На этой основе в следующем параграфе рассмотрена ценность информации в кодонах.

Согласно теориям Эйгена и Куна, химическое и биологиче­ское развитие, т. е. эволюция, идут в направлении возрастания ценности информации, определяемой как селективная ценность. Однако констатация этого положения в модельных теориях еще не означает решения проблемы, т. е. построения количественной физической теории.

Очевидно, что эволюция не могла бы проходить в обозримые сроки, если бы она состояла в непрерывном переборе любых мутантных форм. Все известное нам сейчас о функционировании геномов эукариотов свидетельствует о том, что на данном этапе эволюционного развития возможен большой, но ограниченный набор мутаций, который сужается в ходе дальнейшей эволюции,
но не беспредельно. В этом смысле эволюция есть стохастиче­ский процесс. Реализуются цепи Маркова, описываемые стоха­стическими матрицами, содержащими множество нулей (см. [46]). Иными словами, если какое-либо событие уже осуществи­лось, то вероятности многих последующих событий, которые до того были принципиально возможны, становятся исчезающе ма­лыми. Сама стохастическая матрица эволюционирует в направ­лении сужения набора реализуемых мутаций.

Вследствие полового размножения мы имеем дело с сетью це­пей Маркова. Каждая особь наследует мутировавшие признаки от двух родителей, четырех прародителей и т. д. и оставляет при спаривании с другой особью ряд потомков. Тем самым, родство особей имеет сетчатый характер в пределах вида. Повышение ценности информации, выражающееся в элиминации большого числа вариантов, приводит к физиологической изоляции особей, к возникновению видов. Общая схема происхождения видов, дан­ная Дарвином [5], показана на рис. 9.8. В ней уже отражены описываемые здесь взаимоотношения. «Сетевой» характер взаи­моотношений между эволюционирующими организмами пока­зан на схемах Шмальгаузена [68] (рис. 9.9). Обособление видов означает элиминацию промежуточных форм и определяет темп
эволюции, значительно более быстрый, чем на ранних стадиях химической и биологической эволюции, предшествовавших био­логическому видообразованию. Можно предположить, что раз­ветвление эволюционного древа при видообразовании имеет смысл повышения ценности генетической информации вследствие все большей ее незаменимости. Сравнение ценности и количе­ства информации в конечных ветвях эволюционного древа за­труднительно — в этом отношении млекопитающее столь же со­вершенно и развито, как насекомое.

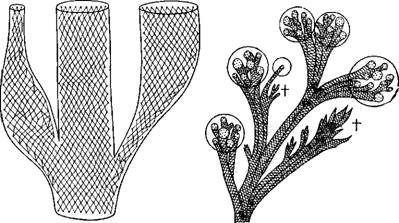
Рис. 9.9. Схемы, показывающие формы реального родства близких организ­мов по Шмальгаузену.

А. Обособление трех видов, из которых один (в центре) биологически стабилен, второй (справа) биологически прогрессивен, третий (слева) находится на пути к вымиранию Особи обозначены точками, поколения — последовательными рядами точек. Б. Родство шести родов с различным числом видов. Имеются вымершие виды и роды, обозначаемые крестом.

Иллюстрируем важнейший для эволюции процесс элимина­ции большинства вариантов внешней аналогией. Шахматист в поисках наилучшего хода в данном положении не перебирает все возможные ходы, удовлетворяющие правилам игры, но от­брасывает подавляющее большинство ходов сразу. Выбор идет всегда между небольшим числом ходов, согласующихся с «усло­виями среды», т. е. со сложившейся на доске позицией.

Развитие партии, подобно биологическому развитию, основы­вается на наличии обратных связей между результатами разви­тия и граничными условиями. Согласно [132] реализуется схема

Неравновесие -> Диссипация -> Неустойчивость и новая струкрура

N. і/

Возрастание диссипации

По мере развития партии число возможных вариантов убы­вает. Начать партию можно многими способами, но в эндшпиле выбор хода почти однозначен.

Аналогия эта, конечно, очень условна. Эволюционирующая популяция обязательно содержит много вариантов, находящихся в согласии с условиями существования. Изменчивость всегда представлена в достаточно широких пределах (см. [99]). Именно этим обеспечивается возможность естественного отбора в ре­зультате изменений условий среды. Соответственно, достаточно широкое разнообразие вариантов в пределах вида поддержи­вается на всех этапах эволюции.

В действительности, поскольку нет «высшего разума», играю­щего эту партию, более перспективны аналогии с играми, осно­ванными на случайных процессах [83].

Эволюция определяется поведением не только популяции, но биоценоза как целого. «Канализация» эволюции возникает в ре­зультате взаимодействия всех популяций растений и животных в данном биоценозе. Мутабильности взаимодействующих видов взаимно связаны. Переходя от стохастического рассмотрения к детерминистическому, основанному на решении дифференци­альных уравнений, мы встречаемся с изменениями во времени не только переменных, описывающих популяции, но и соответ­ствующих граничных условий, в свою очередь зависящих от этих переменных. При этом кинетические уравнения должны решать­ся с учетом запаздывания — состояние данной популяции зави­сит от числа актов размножения. В § 9.11 рассмотрены некото­рые системы такого типа.

Генетические механизмы определяют оптимальную мутацион­ную устойчивость эволюционирующей популяции. Рассмотрение генетических механизмов, проблем популяционной генетики вы­ходит за рамки данной книги. Этим вопросам посвящена фун­даментальная монографическая литература (см. [70—72]).

Здесь высказаны лишь некоторые качественные соображе­ния. Количественная теория эволюции, основанная на информа­ционных подходах, еще не построена.

Представления, изложенные в этом и предыдущих парагра­фах, раскрывают смысл «антиэнтропийности» живых организ­мов. Суть дела состоит не в том, что живые системы имеют вы­сокую упорядоченность, как это считал Моно [74]. Упорядочены и кристаллы, и упорядоченность организма, выраженная в эн­тропийных единицах, невелика (см. стр. 92). Организм отли­чается от кристалла тем, что, будучи сложной открытой систе­мой, находящейся вдали от равновесия, он обладает информа­ционной структурой, развивающейся в пространстве и времени. Живой организм характеризует на всех уровнях строения «па­мять», он «помнит» о своем филогенезе и онтогенезе. Соответ­ственно, понятие энтропии и эквивалентное ему понятие коли­чества информации недостаточны для описания живых систем. Именно в этом смысле организм можно считать «антиэнтропий­ным». Термодинамика оказывается недостаточной с того мо­мента, когда для процесса становится существенным не коли­чество, но ценность информации. Согласно теориям Эйгена и Куна этот момент наступает на стадии образования информа­ционных макромолекул в добиологической эволюции. Конечно, в то же время нет никакого противоречия между существова­нием и развитием жизни и вторым началом термодинамики.