ФИЗИКО-МАТЕМАТИЧЕСКИЕ ОСНОВЫ КИНЕТИКИ НЕЛИНЕЙНЫХ ПРОЦЕССОВ
Определим метод изучения биологической системы как построение кинетической модели и описание модели дифференциальными уравнениями, т. е. как построение математической модели и исследование решений этих уравнений.
Достаточно общая форма математической модели имеет вид
Df dx
(8.6)
,v
Dt
xN),
— Fn (*i. • • •» %)> ,
Где Xi, ..., xN— физические переменные, характеризующие систему и зависящие от времени и начальных условий, Fi, ... .. ., Fn — в общем случае нелинейные функции от этих переменных.
Систему (8.6) можно линеаризовать. Ищутся стационарные значения переменных х..., x°N, являющиеся решениями уравнений (8.6) при Х\ = ... = xN = 0. Далее исследуются линейные уравнения, записанные в переменных, представляющих собой малые отклонения а1=х1 — х°}, ..., aN = xN — хйы\ членами, нелинейными относительно а,, можно пренебречь. В большинстве случаев для интересующих нас задач оказывается возможным ограничиться системами второго порядка (N = 2) (см. [18]).
В соответствии со сказанным целесообразно начать изложение с исследования простой линейной модели — осциллятора
С трением. Его уравнение движения есть уравнение второго порядка
TOC \o "1-3" \h \z mx + bx+ kx = 0, (8.7)
Которое можно представить в форме двух уравнений первого порядка, если ввести вторую переменную — скорость у — х. Тогда получим линейные уравнения типа (8.6)
Vt zi т v т
Общее решение уравнения (8.7) есть
* = Л1ехрА, і/ + Л2ехр V, (8.9) где и Я2 —корни квадратного уравнения
Я2+—А + —= 0. (8.10)
' т. ' т \ • /
При Ь2 > 4km эти корни вещественны, при Ь2 < 4km — комплексны. В первом случае процесс имеет характер апериодического затухания, во втором — затухающих колебаний. Значения А і и Л г определяются начальными условиями.
Рациональный метод исследования кинетической системы состоит в получении ее «фазового портрета». Движение системы представляется движением изображающей точки на фазовой плоскости х, у, где у = х. Точка движется по фазовой траектории с фазовой скоростью. Получим уравнение фазовой траектории для осциллятора с трением, исключив время из уравнений (8.8). Для этого разделим второе уравнение на первое:
Dy 2hy + со їх
"27 е у 1 <8Л1)
Где 2h — bjm, oag= kjm. Уравнение (8.11) описывает интегральные кривые, в каждой точке которых касательная имеет наклон, равный dy/dx. Вместе с уравнением (8.8) уравнение (8.11) определяет на фазовой плоскости некоторое векторное поле с единственной особой точкой х — 0, у = 0. Удобно исследовать это поле с помощью изоклин, т. е. кривых (в данном случае прямых), являющихся геометрическим местом точек, в которых касательные ко всем интегральным кривым имеют одинаковый наклон. В нашем случае уравнение изоклины с наклоном х имеет вид
Dx
Или
СО,2
Y = ax = - TҐwr, (8.12)
Иными словами, изоклины представляют собой прямые, проходящие через начало координат — через особую точку л; = О, у = 0.
2=0
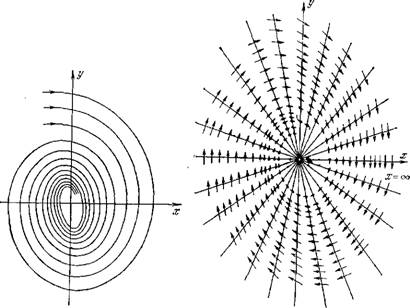
Рис. 8.1. Интегральные кривые Рис. 8.2. Векторное поле для осцилля - на фазовой плоскости для зату - тора с трением,
Хающих колебаний осциллятора с трением.
Решение уравнения (8.11) для случая затухающего колебательного процесса, Ъ2 < 4km или h2<a>2, имеет вид координатного уравнения (см. [8])
У2 + 2Нху + а>у = Сехр[2 arctg JL^L]. (8.13)
Где С — произвольная постоянная, определяемая начальными условиями. Этому уравнению соответствует семейство логарифмических спиралей, показанное на рис. 8.1. Векторное поле, построенное с помощью изоклин, изображено на рис. 8.2. Фазовая скорость находится из уравнения
V^ix + jy, (8.14)
Аа»
Где і и / — единичные векторы.
В нашем случае, согласно уравнениям (8.8), v = iy + j (— 2hy — а>2х)
Ы2 = со**2 + 4 htfxy + (1 + Ah2) у2.
Фазовая скорость убывает по мере приближения к началу координат и обращается в нуль в этой точке.
При h — 0 (т. е. b = 0) трения нет, и система становится незатухающим гармоническим осциллятором. Интегральные
Кривые представляют семейство эллипсов
T/2 + cogx2 = const (8.15)
(см. [8], а также [9], § 1.2). Уравнение изоклин имеет вид у=— а>1х/ус, фазовая скорость задается соотношениями v — iy — j®lx, I v I2 =
~ У2 (Од*2.
Для затухающего апериодического процесса b2> > 4km, т. e. h2 > <в2. Корни характеристического уравнения вещественны и отрицательны:
Я, = - h + д/h2 - и2» \ = - h-^h2-о)2.
Фазовый портрет системы показан на рис. 8.3.
В описанных примерах мы имеем дело с различными типами особых точек, во всех трех случаях расположенных в начале координат х, у. Для гармонического осциллятора без трения все фазовые кривые замкнуты (имеют форму эллипса) и охватывают особую точку, называемую центром. Для затухающих колебаний особая точка является асимптотической точкой всех кривых, имеющих вид вложенных друг в друга спиралей. Такая точка называется фокусом. Наконец, при апериодическом затухании все кривые проходят через особую точку, именуемую узлом. Проведем общее исследование особых точек.
Рассмотрим систему двух нелинейных дифференциальных уравнений типа
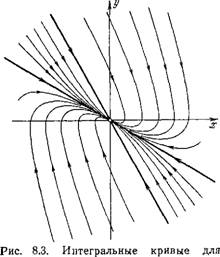
Апериодического затухания осциллятора с трением.
І = щх + а2у + Х2 (х, у), •) y = biX + b2y + Y2(X, у), j {ЬЛЬ)
Где Х2 и Y2 — полиномы, содержащие члены порядка выше первого относительно х и у. Правые части уравнений обращаются в нуль в начале координат х = 0, у = 0. Следовательно это особая точка, отвечающая стационарному состоянию х = у = 0. Ограничиваясь линейным приближением, т. е. рассматривая лишь окрестность этой точки, имеем
![]()
Dy __ Ь, х + Ь2у dx а\Х + агу '
Интегральная кривая есть
И решение уравнения (8.17) имеет вид
Х = А\ ехр %it + Л2 ехр у = В\ ехр V + В2 ехр h2t,
Где Я, и Я2 — корни характеристического уравнения
К2 — (а\ + Ь2) Я + axb2 — a2bi = 0.
Это полностью соответствует изложенному выше (в случае ое - і циллятора с трением было а, = 0, а2 = 1, = — cog, Ь2= —2h). Общая классификация особых точек, данная Пуанкаре [10], основывается на поведении интегральных кривых в ближайшей окрестности этих точек.
Если дискриминант характеристического уравнения D = = — 4a2bi—(ai — b2)2^Z 0, то оба корня Яь Я2 вещественны. Если одновременно аф2 — a2bt > 0, то их знаки одинаковы. Рассмотрим следующие случаи:
/. Яь Яа < 0. Решение имеет вид убывающих экспонент, т. е. система, выведенная из особой точки, в нее возвращается. Особая точка есть устойчивый узел. » 2. Яь Я2 > 0. Система удаляется от особой точки, представ
Ляющей собой неустойчивый узел.
D ^ 0, но a,\b2 — a2bi < 0. Корни Яі, Яг имеют разные знаки. Особая точка является неустойчивой и именуется седлом. Через нее проходят только две интегральные кривые, называемые сепаратрисами. Остальные фазовые траектории уходят в бесконечность, минуя особую точку.
D < 0, но аф2 — a2bi = 0, т. е. D = ~{ах + Ь2)2, Я, = 0, Я2 = at - J - b2. Один из корней равен нулю. Для линейной системы (8.17) получается не особая точка, но прямая, соответствующая равновесным состояниям, в которую упираются остальные интегральные прямые, направления движения по которым зависят от знака Яг.
Если дискриминант D > 0, то корни Лі и к2 комплексно сопряжены.
Вещественные части Лі, к2 отрицательны, т. е. а\ + Ь2 < 0. В системе происходят затухающие колебания, особая точка, на которую накручиваются спиральные фазовые траектории, есть устойчивый фокус.
Вещественные части Ль положительны, т. е. а\ + Ъ2 > 0. Особая точка есть неустойчивый фокус, соответствующий нарастающим по амплитуде колебаниям.
Корни Лі = — k2 мнимые, т. е. а\ + Ъ2 = 0. В системе происходят незатухающие колебания, особая точка есть центр. Фазовые траектории представляют собой концентрические эллипсы.
(8.19)
(8.20)
Виды особых точек, соответствующих случаям 1, 3, 6, 7, показаны на рис. 8.4 [8, 11]. В рассмотренном случае особая точка
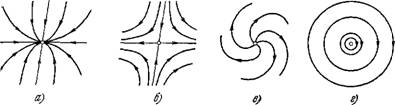
Рис.- 8.4. Типы узловых точек иа плоскости состояний.
А—устойчивый узел, 6—седло, в—неустойчивый фокус, г — центр.
Типа седла невозможна. В самом деле, условия ее появления для осциллятора имеют вид 4h2 — 4со2 >0 и со2 < 0, что лишено физического смысла при положительных значениях ^ и га, Особая точка типа седла имеется, например, в случае линейной системы, в которой действует сила отталкивания от положения равновесия, причем величина этой силы возрастает со смещением. Так ведет себя, в частности, математический маятник вблизи верхнего положения равновесия. Уравнение его движения имеет вид
G
Ф-Т-Ф = 0
Где ф — угол, отсчитываемый от верхнего положения равновесия, g— ускорение свободного падения, / — длина маятника. Перепишем это уравнение в виде
Х — пх — 0,
Или
Х = У, У — пх.
Здесь а{ = 0, а2 = 1, bi = п, Ь2 — 0 и условие 3 (см. стр. 401) соблюдается: An > 0, —я < 0. Уравнение
Dy х
Dx П у
Легко решается. Интегральные кривые отвечают уравнению семейства равносторонних гипербол
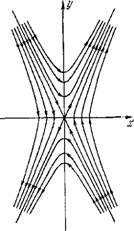
У=-л/пх
У-у/п X
Рис. 8.5. Фазовый портрет для осциллятора с отрицав тельным трением.
У*-пх2 = С (8.22)
С асимптотами у = — л/пх и у—л/пх. Эти кривые показаны на рис. 8.5. Особая точка х = 0, у — 0, находящаяся на пересечении асимптот, является седлом.
Таким образом, особая точка изображает состояние равновесия или стационарное состояние системы. Мы уже говорили об устойчивых и неустойчивых особых точках. Определение устойчивости состояния равновесия по Ляпунову [12] гласит (см. [8], [9], § 1.2):
(8.21)
«состояние равновесия устойчиво, если для любой заданной области є допустимых отклонений от состояния равновесия имеется область б(б), окружающая это состояние и обладающая тем свойством, что ни одно движение, начинающееся внутри б, никогда не достигает границы области е.» И наоборот, состояние равновесия неустойчиво, если имеется область б, для которой область б (б) не существует. Пусть на фазовой плоскости область б есть квадрат; тогда состояние равновесия х = х0, У = Уо устойчиво, если, задав наперед сколь угодно малое положительное значение б, можно найти такое б (б), что если при / = 0
I * (0 — *0 i < б
|*(0)-Хо1<8 и I у (0) — Уо I < б, то для 0 < / < оо
I У (0 — Уо I < Б.
Легко показать, что в рассмотренных случаях фокус и узел устойчивы. Гармонический осциллятор без трения совершает незатухающие колебания вокруг состояния равновесия, чему со
ответствуют движения изображающей точки по концентрическим эллипсам. Согласно данному определению устойчивости особая точка типа центра всегда отвечает устойчивому состоянию оан - новесия [8].
Фокус отвечает неустойчивому состоянию, если трение отрицательно, т. е. h -< 0. Такая ситуация реализуется, например, в ламповом генераторе (см. [8]). При этом спирали не свертываются в фокус, но развертываются из него. Аналогичным образом, при большом отрицательном трении, когда h <; 0, /?2 > > а2, возникает неустойчивый узел. Седло отвечает неустойчивому состоянию.
Теория нелинейных динамических систем различает «грубые-» и «нзгрубые» системы [8]. В первом случае малые изменения параметров системы не изменяют ее общего поведения — математическая модель устойчива го отношению к малым изменениям вида дифференциальных уравнений. Ситуации, отвечающие пунктам 1, 2, 3, 5, 6 приведенной выше классификации, характеризуют грубые системы. Напротив, в случаях 4 и 7 системы негрубые. В самом деле, в случае 4 значение параметра а\Ь2— аф\ = 0 является критическим, при переходе от его положительной к отрицательной величине вместо устойчивого узла возникает седло. В случае 7 критическим является значение параметра а\ - f - b2 = 0 — при переходе - j - b2 > 0 -*■ а{ b2 — 0 -> а\ b2 < 0 особые точки изменяют свой характер:
Неустойчивый фокус —> центр —*■ устойчивый фокус.
Такие критические значения параметра являются бифуркационными.
Проблемы теории устойчивости и методы исследования устойчивости динамических систем подробно рассмотрены в ряде монографий [8, 11 —18]. Краткое введение в рассматриваемую здесь область дано в [17—19].
Из приведенного рассмотрения линейных систем следует важный общий вывод. Среди них только гармонический осциллятор без трения характеризуется замкнутыми фазовыми траекториями, отвечающими периодическому движению. Периодические процессы невозможны для линейных неконсервативных систем.
Обратимся теперь к нелинейным системам. Колебательное поведение нелинейных систем весьма разнообразно и сложно. Его изучение имеет фундаментальное значение для очень широкого круга физических проблем. Физика нелинейных колебаний развита в трудах школ Мандельштама (см. [о, 20—22]), Ван-дер-Поля [23] и др.
Очевидно, что общие уравнения (8.6) нелинейны; то же относится к уравнениям (8.16), которые мы линеаризовали с целью
исследования окре - тностей особых точек. Но такое исследование ке. дает ответа на вопросы о поведений нелинейной системы кл чсей фазовой плоскости.
(8.23)
Нелинейная система может характеризоваться наличием ряда особых точек, отвечающих устойчивым и неустойчивым состояниям. Если система консервативна, то ее уравнения движения имеют интеграл энергии
7 itf + u(x) = &,
Где константа интегрирования & зависит от начальных условий, у2/2 — тх2/2 есть кинетическая, a U (х)—потенциальная энергии. Движение изображающей точки зависит от соотношения между U (х) и S. Рассмотрим на плоскости х, z кривую 2 = = U (х) и прямую г = &. Возможны следующие случаи [8]:
Прямая z — & не пересекает кривую U(x). Если точки кривой лежат выше точек прямой, то на фазовой плоскости нет движения с полной энергией &. Если прямая г — & лежит выше кривой z— U (х), то на фазовой плоскости х, у имеются дзе симметричные ветви фазозой траектории, по которым изображающие точки уходят в бесконечность (убегающие траектории) .
Прямая z — & пересекает кривую z— U(x). Для значений х, для которых U(x)~>^, фазовых траекторий нет, для остальных значений х существуют как убегающие, так и замкнутые ветви, отвечающие периодическим движениям.
(8.24)
(8.25)
Лрямая z — & касается кривой г = U(x). Фаговые кривые на плоскости х, у разбиваются на несколько классов. Возможны изолированные точки, вблизи которых нет ветвей фазовых кривых, отвечающие устойчивым состояниям равновесия. Возможны изолированные конечные участки фазовых кривых — замкнутые кривье или кривые, с самопересечением. Последние являются так называемыми сепаратрисами, т. е. кривыми, проходящими через особые точки типа седла (рис. 8.6). Сепаратрисы разделяют области, заполненные кривыми различных типов. Поэтому нахождение сгпаратрис очень важно для определения поведения системы. .Наконец, возможны бесконечные участки фазовых сривых. Пример нелинейной консервативной системы — маятник, выполняющий большие колебания без трения и описываемый уравнением движения
/ф - f mgl Біпф — 0,
Где /—момент инерции маятника. При наличии трекия /6 + 'оф - f - mgl sir. ф == 0,
Система уже неконсервативна и интеграла энергии не имеет. Уравнение баланса энергии имеет вид
І = _ Ьф2 < 0. (8.26)
Энергия убывает при движении системы, стремясь к некоторому равновесному значению — ф стремится к нулю.
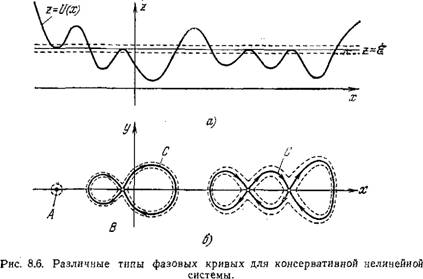
А —кривая г = £/ (х) и прямая z—% на плоскости х, г; б —фазовые траектории на плоскости х, у, Л — изолированная точка, В— изолированные участки фазовых кривых,
С — сепаратрисы.
Уравнение (8.24) можно переписать в виде
Ф = со, со = — mg/sincp//. (8.27)
Фазовые траектории удобно изобразить на развертке цилиндра на плоскости со, ф в виде полосы шириной 2я. На рис. 8.7 показаны кривая г = U(ф) = — mgl cos ф на плоскости ф, z и фазовый портрет системы. Имеются особые точки двух типов — центр (о = 0, ф = 0 и седла со = 0, ф = ± я, через которые проходят сепаратрисы. При — tngl <. 8 < tngl маятник колеблется около нижнего положения равновесия, около центра. При <§ = mgl получается интегральная кривая, проходящая через седло, т. е. состоящая из седла и сепаратрис. Седлу соответствует верхнее неустойчивое положение равновесия. При <8 > > mgl кривые соответствуют вращательным движениям маятника.
Для неконсервативной системы (8.25) картина на развертке фазового цилиндра описывается уравнением dw _ 6а + mgl sin ф
— Ти • (8-28>
Особые точки ф = 0, а = 0иф = ±я, со = 0. Точка (0, 0) есть устойчивый фокус (если Ь2 < 4/ mgl) или устойчивый узел (если Ъ2 > 4/ mgl). Точки (±я, 0)—седла. Периодических движений
Нет, система стремится к устойчивому равновесию.
Особый интерес для биологии р представляют автоколебательные системы, в которых устанавливаются и поддерживаются неза-
ПрейтныИ цикл
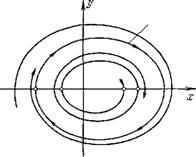
Рис. 8.7. Фазовый портрет не - Рис. 8.8. Предельный цикл,
Линейных колебаний маятника. Л —центр, В— седло, С — сепаратрисы.
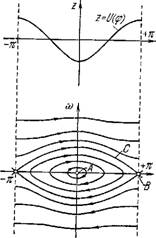
Тухающие колебания несмотря на наличие трения. Это происходит за счет сил, зависящих от состояния движения самой системы. Размах автоколебаний определяется свойствами самой системы, а не начальными условиями. Из неустойчивых особых точек фазовые траектории уходят в бесконечность или к устойчивым особым точкам. Кроме того, именно в случае автоколебаний эти траектории могут «накручиваться» на замкнутую кривую, охватывающую особую точку, — на предельный цикл (рис. 8.8). В свою очередь, предельные циклы могут быть устойчивыми или неустойчивыми. Эти ситуации присущи грубым системам, к которым относятся, по-видимому, системы биологические [18]. Устойчивый предельный цикл соответствует незатухающим автоколебаниям. С таким явлением мы уже встречались при обсуждении свойств летательных мышц насекомых (см. § 5.10). Нахождение предельных циклов на фазовых портретах есть важный момент исследования нелинейных систем.
Классический пример автоколебаний — явления, происходящие в ламповом генераторе (см. [8, 20]). В дальнейшем изложении рассмотрены соответствующие химические и биологические явления.
Подробное рассмотрение нелинейных колебательных процессов и применения теории к ряду конкретных систем — преимущественно механических и электрических—приведены в [8, 1І, 15—18]. Рассмотрим теперь некоторые химические системы, исследование которых оказывается связанным с биологией. Мы видели, что принципиальные подходы к химическим системам те же, что и в механике, и в учении об электричестве. Это с особенной ясностью демонстрируется в термодинамике сетей (см. стр. 79). Особенности химических и биологических систем состоят в следующем.
Динамическими переменными в химии и в ряде биологических проблем являются концентрации реагентов. На той же основе в качестве переменных рассматриваются числа организмов (в популяционной генетике и в экологии).
В химико-биологической системе химические процессы зачастую связаны с диффузионными, с транспортом вещества. Иными словами, здесь мы встречаемся не с точечными, а с распределенными системами. Особое значение для биологии имеет компартментализация — подразделение системы на «отсеки», разделенные мембранами. Система пространственно гетерогенна.
В химических системах живой природы нелинейные химические реакции сопряжены как с транспортом вещества, так и с механическими и электрическими процессами.
Во многих химико-биологических процессах приходится иметь дело с малым числом молекул или макромолекул. Как отмечено в [18], само понятие концентрации имеет здесь ограниченную применимость, и в качестве динамических переменных вводятся вероятности тех или иных состояний молекул и макромолекул.
В целом в химии и биологии возникает самое разнообразное нелинейное и, в частности, колебательное поведение. Прямые экспериментальные и теоретические исследования при помощи простых моделей проведены пока лишь для немногих случаев. Однако полученные результаты очень поучительны и обещают многое.