ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ФИБРИЛЛЯЦИЯ ВОЗБУДИМОЙ СРЕДЫ

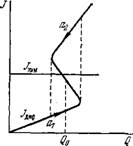
Рис. 8.40. Кооперативное изменение проницаемости мембраны при Q = Q0.

Из изложенного в гл. 5 очевидно, что любая мышечная ткань представляет собой возбудимую среду, — возбуждение, сообщае­мое сетью нервных волокон, вызывает механохимические про­цессы. Тем самым процессы в возбудимых средах имеют важ­нейшее значение для физиологии, в частности, для физиологии сердечной мышцы. Рассмотрим, следуя работам Кринского ([79, 95—99], см. также [19]), фибрилляцию сердца. При некоторых патологических состояниях ритмически сокращающаяся сердеч­
ная мышца десинхронизуется, отдельные мышечные волокна со­кращаются хаотически, асинхронно, наступает фибрилляция, приводящая организм к гибели. Спасение может быть достиг­нуто лишь быстрой дефибрилляцией, возвращением сердца к его нормальному ритму. Физическая задача состоит в анализе при­роды фибрилляции и условий ее возникновения, в нахождении таких параметров системы, при воздействии на которые сердце можно перевести в нормальный режим.

В § 8.5 рассмотрены возбудимые среды, в которых протекают химические реакции. Визуально наблюдаемые в таких средах автоволновые процессы свойственны возбудимым средам в це­лом. В частности, циркуляция возбуждения в двумерной системе приводит к общему для возбуждаемых сред явлению — к воз­никновению ревербераторов.

Само понятие возбудимой среды как среды, в которой рас­пространение импульса происходит без затухания, было введено Винером и Розенблютом [42]. Импульс генерируется каждой точкой среды. Примером одномерной возбудимой среды может служить бикфордов шнур или нервное волокно. Каждая точка возбудимой среды может находиться в одном из трех состояний: покоя, возбуждения и рефрактерности. Если на точку, находя­щуюся в состоянии покоя, подать возбуждающий сигнал, то она перейдет в возбужденное состояние, в котором пробудет время X, затем перейдет в рефрактерное состояние, продолжающееся в течение времени тr. В период рефрактерности тв точка не реа­гирует более на возбуждающий сигнал, следовательно, никакая точка не может возбуждаться с частотой, большей т^1.

Общие математические модели возбудимых сред, объясняю­щие возникновение ревербераторов, рассмотрены в работах [19, 42—45, 100]. Показано, что синхронное распространение волн может нарушаться в результате появления источников волн, вы­званного попаданием в среду внеочередного (экстрасистоличе­ского) импульса возбуждения. В неоднородных средах эти источники могут размножаться и порождать фибрилляцию.

Ревербератор в однородной двумерной системе возникает, например, при наличии отверстия, периметр которого превышает длину волны Я = vxR (v — скорость распространения волны). Циркуляция волны возбуждения возможна и в непрерывной среде, неоднородной по рефрактерности. Если в некоторую об­ласть среды, имеющую форму кольца, послать импульс, то он не будет циркулировать, так как волны возбуждения, распро­страняющиеся по часовой стрелке и против нее, встретятся и погасят друг друга. Однако если рефрактерность не всюду оди­накова, то циркуляция возникнет вследствие трансформации ритма.

На рис. 8.41 показана неоднородная среда, состоящая из двух областей с периодами рефрактерности тді и тД2- Интервал At между двумя последовательными волнами ai и а2 таков, что

\а,

А А а А

^Rt

Т-Х2

А)

Рис. 8.41. Трансформация ритма в двумерной неоднородной среде.

Л —распределение рефрактерности разрыв фронта волны а2.

Волна а2 не может возбудить область с периодом рефрактерно­сти ти2 > Tri. Возникает разрыв фронта волны а2. Рефрактер­ный «хвост» имеет большую длину в области 2, чем в 1. Транс­формация ритма состоит в выпадении второго импульса.

Ревербератор возникает при контакте фронта волны с покоя­щейся тканью. Такая ситуация создается, например, встречной

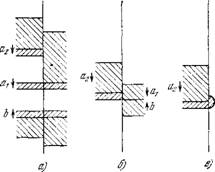
Рис. 8.42. Возникновение ревербератора в неоднородной среде.

Последовательные стадии а, б, в, г

Волной b (рис. 8.42). Волны b и ai гасят друг друга, и волна а2 переходит в правую полуплоскость в виде полукруга (рис. 8.42, в), а затем, миновав свой «рефрактерный хвост»,— в левую. Путь замыкается, и образуется ревербератор (рис. 8.42, г).

В однородной среде период волн, посылаемых реверберато­ром, равен тд, и ревербератор существует неограниченно долго.

Если он возник на границе двух однородных областей, то его время жизни конечно и тем меньше, чем больше неоднород­ность. Число оборотов волны возбуждения вокруг линии раз­рыва фаз равно

Размер ревербератора может быть меньше длины волны.

Ревербераторы могут сами служить источником волн высо­кой частоты, вызывающих появление новых ревербераторов. Иными словами, возможен процесс размножения реверберато­ров. В неоднородной среде ревербераторы посылают волны с различными частотами и не синхронизуются. Если новые источники волн рождаются чаще, чем исчезают старые, то на­блюдается сложная картина, напоминающая фибрилляцию.

Другой источник волн, не связанный с циркуляцией возбуж­дения, представляет собой так называемое эхо. Если подать не­сколько импульсов на неоднородное по периодам рефрактерно - сти волокно, то на неоднородности появляются новые импульсы, бегущие по волокну, и лишь позднее наступает состояние покоя. Возникшие импульсы подобны отраженным от неоднородности, которая рассматривается как источник эха. Кринский исследо­вал условия возникновения эха, характеристики соответствую­щего источника и их зависимости от параметров среды. Пока­зано, что эхо может появляться в средах, удовлетворяющих условию т/тr > '/2. Начальные условия состоят в наличии доста­точно большого разрыва в распределении фаз элементов по воз­будимой среде. В неоднородной среде разрыв может возникать при трансформации ритма. Свойства источников эха близки к свойствам ревербератора, за исключением того, что размер источников эха может быть как угодно мал.

Ревербератор есть источник импульсов, который может су­ществовать в среде и при т/тд < '/г - Пути, по которым возбуж­дение переходит из области с меньшей рефрактерностью в об­ласть с большей рефрактерностью и обратно, пространственно разделены, но сближаются при увеличении т/тд и при т/ти ^ !/г соединяются. Тем самым эхо представляет собой предельный случай ревербератора с нулевой длиной. Эхо и ревербератор обладают одинаковыми свойствами как источники импульсов и могут быть причинами фибрилляции в неоднородных возбуди­мых средах.

В электрофизиологии состояние сердечной ткани характе­ризуется так называемой «зоной уязвимости». Уязвимость озна­чает возникновение более чем двух ответов при подаче на по­лоску миокарда двух импульсов. Шириной зоны называется ди­апазон интервалов между импульсами At, при которых возни­кает уязвимость. Крииский показал, что уязвимость опреде­ляется величиной х' = т/тн, ширина зоны тем меньше, чем меньше т'.

В неоднородной возбудимой среде возникший источник волн, будь то эхо или ревербератор, может служить стимулятором для запуска новых источников волн. Если параметры среды таковы, что скорость «размножения» источников не меньше, чем ско­рость их «умирания», то возможна фибрилляция. При взаимо­действии нескольких источников длительность фибрилляции быстро растет с увеличением т'. Минимальное число источников, способное вызвать фибрилляцию заданной длительности, умень­шается с увеличением х'. Опыт показывает, что на полоске ткани миокарда фибрилляция может быть длительной, если размеры самой полоски достаточно велики, т. е. имеется некоторая «кри­тическая масса» для фибрилляции. Очевидно, что число источ­ников, обеспечивающее фибрилляцию, является аналогом кри­тической массы.

Основной вывод, полученный Кринским, состоит в том, что безразмерный параметр х' является важной характеристикой возбудимой среды, определяющей режим фибрилляции и время его существования.

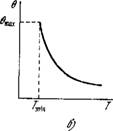
Применительно к сердечной мышце в целом необходимо найти аналог величины т, выражающей длительность возбуж­денного состояния, который можно измерить электрофизиологи­ческими методами. В качестве такой величины вводится время возникновения ответа на подаваемый импульс, т. е. латентный период 0. Известно, что чем меньше амплитуда импульса, по­даваемого на одиночную клетку, тем позже появляется ответ. При возбуждении двумя фиксированными стимулами 0 зависит от времени Т, прошедшего после последнего возбуждения клетки к моменту прихода стимула (фаза клетки). Зависимость 0 от амплитуды раздражения показана на рис. 8.43, а, зависимость от фазы клетки Т—на рис. 8.43,6. Существует максимальная задержка 0Шах, т. е. ответ не появляется при подпороговых сти­мулах А < Лт1п и при Т <jTmm - Если клетка возбуждается не стимулятором, а соседней клеткой, то при известном расстоянии между клетками график на рис. 8.43, б позволяет определить скорость распространения возбуждения. Функция 0(Г) описы­вает распространение возбуждения в системе. Теоретический анализ показывает, что каждому значению 0 отвечают два зна­чения скорости распространения возбуждения. Большая скорость характеризует устойчивый процесс «горения», меньшая — не­устойчивое «тление», не наблюдаемое при периодическом следо­вании импульсов в стационарном режиме. При увеличении ча­стоты следования импульсов меньшая скорость возрастает, а большая уменьшается. При дальнейшем повышении частоты
обе скорости совпадают, режим становится нестационарным и происходит периодическое выпадение импульсов.

Возникновение ревербераторов облегчается при увеличении параметра Эшах/тн. Если этот параметр больше '/г, возможно возникновение источников эха.

Таким образом, величина 0/тн (тд — период рефрактерности) определяет уязвимость сердечной мышцы (см. стр. 456). При­меняемые в медицине антиаритмические вещества, дефибрилля­торы, влияют именно на этот параметр. Важный для практики

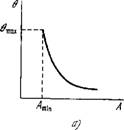
Рнс. 8.43. Зависимость латентного периода от амплитуды раздражения (а) и его зависимость от времени, прошедшего после возбуждения (б).

Результат теоретического исследования состоит в том, что най­дены физические критерии антиаритмогенных воздействий, кото­рые могут изучаться на тканевых моделях путем определения изменений 0/тд. На тех же основаниях исследуются факторы, вызывающие фибрилляцию. Действительно, удалось показать экспериментально, что вещества, уменьшающие 0/тд, обладают антиаритмическими действиями, а вещества, увеличивающие это отношение, напротив, способствуют возникновению сердечных аритмий, в соответствии с тем, что в моделях возбудимых сред уменьшение 0/тн затрудняет возникновение источников волн — эха и ревербераторов.

Более детальное количественное рассмотрение исходит нз математической модели передачи возбуждения по системе электрически связанных клеток. Прежде всего нужно устано­вить, какими свойствами клеточных мембран определяется величина ©шах-

Поведение одиночной возбудимой клетки можно описать си­стемой уравнений

8ф = /(ф, /) + /„„(/), 1 ,0,,сч

/-*<ф./). І (8Л15)

Здесь є — малый параметр, <р — мембранный потенциал, I — ионный ток, /вн — внешний импульс тока. Функции / и g таковы,

Что фазовый портрет системы при /Вн = 0 характерен для воз­будимой мембраны. Изоклина /вн = 0 имеет N-образную форму, с единственной особой точкой О, под действием деполяризую­щего тока изоклина, отвечающая ф = 0, смещается вверх.

Поведение двух связанных клеток описывается уравнениями

Ефі = / (фі, /і) + а (ф, — ф2), J

'Г'1"'!* , , (8.116)

Еф2 = f (ф2, /2) - f а (ф2 — фі), J

І 2 = g{<P2, h)- )

Член а(фі — ф2) представляет ток /вн. текущий через клетку 2 от клетки 1.

Если в момент t = 0 клетка 1 находится в состоянии, соот­ветствующем появлению потенциала действия (ПД), то ток, те­кущий из клетки 1 в клетку 2, может вызвать в ней ПД. На­чальное состояние клетки 2 определяется следующим: возникает ли в ней ПД и через какое время после t = 0. Задержка 0 есть время от t = 0 до возникновения ПД в клетке 2. В норме 0<t (т — длительность ПД), так как в момент t = 0 клетка 2 находится в покое. Если режим аномален, т. е. импульсы по­даются с высокой частотой, то в момент возбуждения клетки 1 клетка 2 может оказаться в рефрактерном состоянии. В резуль­тате либо блокируется передача импульса от клетки 1 к клетке 2, либо ответ возникает с большой задержкой 0max ~ т. Второй случай особенно опасен для миокарда, так как при этом воз­можно возникновение экстрасистол. Большие задержки ответа могут происходить в клетках, в которых постоянный ток может вызвать автоколебания.

Таким образом, задача о задержках сводится к изучению па­раметров клеточной мембраны, определяющих ее поведение под действием деполяризующего тока.

Систему уравнений (8.116) можно переписать в виде

Ефі=/(фі, /і) — аф2, І\ — S(Фь /і),

Єф2 = /(ф2, /2) — Яфь

/2=ё(Ф2, h), где

/(Фь //) == f (Ф/, /Л + афь i=l,2.

Внешний ток, поступающий в клетку 2, задается теперь сле­дующим образом:

(8.117)

/в Н«=-яФі(0. (8.118)

Пусть фі есть прямоугольный импульс; тогда

'-«-{оГ ',5:; <8Л19>

Где 1А = ЯфА, Фа — амплитуда ПД, т — его длительность. Имеем систему

«Ф=?(ф, />+/„«>, 1

/=«№,'), )

И /вн(0 определяется выражением (8.119).

Фазовые траектории для клетки 2 показаны на рис. 8.44.

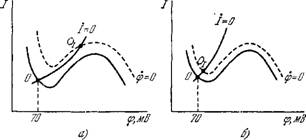
Рис. 8.44. Нуль-изоклины для клеток с большими (о) и малыми (б) задерж­ками.

Пунктир —изоклина при q>=0 при пропускании деполяризующего тока, а —особая точка Oj

Неустойчива, б—устойчива.

Если точка Ог устойчива и находится на левой ветви изо­клины при ф = 0, задержки отсутствуют. Для возникновения больших задержек существенно, чтобы под действием тока не оставалось особой точки на левой ветви изоклины при ф = 0. Большие задержки будут наблюдаться и в тех случаях, когда под действием тока особая точка О/ смещается на правую ветвь и возникает устойчивая деполяризация. Для уменьшения за­держки надо менять параметры мембраны так, чтобы особая точка Oj под действием тока оставалась на левой ветви. Можно, скажем, увеличить наклон изоклины при ф = 0. Таким образом, теоретический анализ позволяет сформулировать требования к веществам — антиаритмикам.

Кринский проанализировал также режим эха в теоретиче­ской модели мембраны. Эхо возникает, если в мембране под действием внешнего тока небольшой величины возникают по­вторные ответы, причем длительность импульса составляет не менее половины периода автоколебаний. Теория Кринского осно­вана на широком применении метода фазовых портретов, отве­чающих модельным уравнениям, описывающим мембранные системы.

Теория фибрилляции сердечной мышцы, исходящая из общих положений физики нелинейных колебательных систем, является прекрасным примером биофизического исследования, доведен­ного до важных практических приложений. Задачи физиологии четко сформулированы здесь как физические проблемы. Это краткое изложение показывает, что именно физический подход к физиологии обеспечивает строгость и общность анализа и под­линное обоснование получаемых выводов.