ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

АВТОКАТАЛИТИЧЕСКИЕ ХИМИЧЕСКИЕ СИСТЕМЫ

В биологии особое значение имеют автокаталитические хи­мические системы. Достаточно указать, что авторепродукция КДеток и организмов эквивалентна автокатализу.

Вернемся сначала к феноменологическому термодинамиче­скому рассмотрению. Как мы видели, для химических процессов критерий эволюции выражается условием (ср. (8.3))

D*a = Т Z Vl Ші ^ 0 (8,29)

І

И условие устойчивости стационарного состояния имеет вид

£ 6с,- Ь£Фі > 0. (8.5)

І

Из (8.29) следует, что вблизи стационарного состояния

Гб^с = Ц бс,-d (б^г)<0. (8.30)

І

Разлагая бсг в ряд по bs4-!t получаем

БС( = £ L'u ШІ, (8.31)

/

Где

Г' dvl

Причем производные взяты для стационарного состояния. Во­обще говоря, Lij может содержать как симметричную, так и антисимметричную часть. В условиях линейности, т. е. вблизи равновесия, коэффициенты Ьц совпадают с коэффициентами Онзагера Lij и антисимметричные их части равны нулю. Вдали от равновесия это также возможно. Тогда

Tdxa = < 0, ' (8.32)

Где

Ч' = 'A Z L-jbsti б а, (8.33)

І,1

Есть кинетический потенциал. Однако если антисимметричные части L'a отличны от нуля, то в общем случае кинетический по­тенциал не существует. Допустим, что два химических процесса описываются чисто антисимметричной матрицей Lijt т. е.

L\\ = Z-22 = 0, L\2 = — Li\ = — L.

Тогда

Tdxa = U (6^2 das4-\ - б^, dbst2) < 0. (8.34)

Такая система вращается вокруг стационарного состояния, не попадая в него. Фазовая диаграмма имеет вид, показанный на
рис. 8.9; точка, отвечающая стационарному состоянию, есть центр. Вводя полярные координаты г и ср на плоскости 2,

Имеем

Tdxa = - L'r2 dtp < 0. (8.35)

Но функция Y = L'r2ф не является кинетическим потенциалом вследствие своей многозначности — она возрастает на 2nL'r2 при каждом обороте [1].

Антисимметричность феноменологических соотношений вы­ражает нелинейность.

Рассмотрим нелинейную систему химических реакций — мо­дель колебательной химической системы, впервые исследован­ную Лотка ]24]

TOC \o "1-3" \h \z ^ (I)

О

X + Y«=*2Y, (II)

К-2

Г Y^fE - (Ш>

Кр^г 8с9Тац°ИоРн^неого со" Глобальная реакция" есть А^Е. Про - стояния антисимметрич - иесс автокаталитическии на стадии (II). иой химической систе - Считаем, что вещество А присутствует в мы [1] избытке, и поэтому реакция (I) нуле­

Вого порядка. Общее сродство, отвечающее глобальной реакции,

= + + = ^^ ■ (8.36)

Вблизи равновесия система линейна:

^01 = kt ^щг, Vq2 = k2XeqYeq -j^r, u03 — k$Yeq. (8.37)

Условие устойчивости имеет вид

Ft, (6j*,)2 + k2XeqYeq (6^2)2 + k3Yeq (б^з)2 > 0. (8.38)

Вдали от равновесия можно пренебречь обратными реакциями, т. е. положить k-\ = k-2 = k-ъ = 0. Следовательно, оо. Ки­нетические уравнения антисимметричны

DY dt dE

(8.39)

=k2XY-kzY,

DX

Dt--kx-k2XY,

Единственное стационарное решение отвечает условию X — = У = 0. Имеем

X° = k з/й2, Y° = kl/k4.

Модель Лотка сходна с моделью «хищник — жертва», исследо­ванной Вольтерра [25] (подробный анализ см. также в [261). В некотором замкнутом районе живут хищники и их жертвы, скажем, рыси и зайцы. Рыси питаются только зайцами, зайцы питаются растительной пищей, имеющейся всегда в избытке. Число жертв Хи число хищников Х2. Изменения численности по­пуляций со временем описываются уравнениями

= kxXx — kXiX2, ]

DXt, I (8-4°)

H X\X2 — k2X2. J

Dt

Константа fei характеризует размножение жертв, k — их убыль вследствие встреч с хищниками, k' — размножение хищников, для которого необходимо питание, т. е. встречи с жертвами, k2 — вымирание хищников. Все коэффициенты k\, k, k', k2 поло­жительны.

Проведем рассмотрение системы Вольтерра — Лотка в этом простом случае (см. [1, Ю, 26], а также [8], стр. 164). Найдем стационарные значения X? и Х2. Из уравнений (8.40) при Х\ = Х2 — 0 получаем

X\ = k2\k', Xl = kjk.

Представим значения Х\, Х2 в виде

X^joexpa;, X2 = X°expa2. (8.4-1)

Очевидно, что a, i = In (Xi/Xf) являются мерой отклонения Xt от стационарного состояния, в котором aj = 0. Уравнения (8.40) перепишутся в виде

А, = 1 ехр а2), ] , \ (8.42)

= 1-ехра,). J

Умножим первое уравнение на expotj), второе —на

—ехра2) и сложим:

4" (1 - ехр а,) + jr Х°2а2 (1 - ехр а2) = 0, (8.43)

Или

Ж [т (ехр а» - а0 + "F ^ (ехр - N] =

Т. е.

Y (ехра, — а,) + (ехр а2 — а2) = К = const. (8.44)

Величина К есть постоянная движения. Оба члена в К положи­тельны, так как если а* > 0, то ехр а* > осі, а если осі < 0, то

Рис. 8.10. Построение интегральных кривых для модели Вольтерра —

Лотка [26].

Объяснение в тексте.

Ехр а і > 0. Следовательно, К > 0. Введем обозначение ехр аг = = Pi. Умножив обе части (8.44) на kk', имеем, так как k'X\ = &21 kX°2 = klt

K2 (ft - In p,) + kx (Pj - In Pa) = Kkk'\ откуда, поделив на kxk2, находим

X Ф. - In ft) + £ № - In р2) - К = const.

Потенцирование дает

(р, ехр (- р,))№ (ft ехр (- р2))№ = UtU2 = const. (8.45)

Уравнение U\U2 = const есть уравнение гиперболы. Ее график показан на рис. 8.10, а. На рис. 8.10,6 и в показано поведение U2 и V\ как функций р2 и ft соответственно. Кривые t/i(ft) и U2($2) имеют максимумы. Зависимость р, от р2, следующая из (8.45), показана на рис. 8.10, г Максимумам IJ\ и U2 отвечают точки В и А на гиперболе. При движении между этими двумя
предельными точками на плоскости Pi, р2 описывается цикл. Характер цикла зависит от начальных условий. Стационарному состоянию соответствуют точки А и В на гиперболе, точки мак­симумов М\ и М2 на кривых Ј/i(Pi) и U2(Р2) и особая точка типа центра на плоскости рь р2. Определим поведение системы вблизи

(8.47)

J6V

$8 120

І I

T80

1

J 47

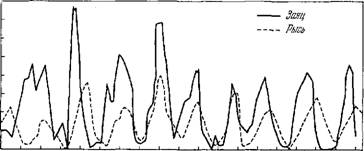
1845 1855 1855 , 1875 1885 1895 1905 1915 1925 1935 Рис. 8.11. Динамика популяций зайцев и рысей в Канаде за 1845—1935 гг.

Особой точки. Линеаризуем систему (8.40), т. е. будем искать ее решение в виде

*,(/) = Я?+ 6JT, ехр (W), Х2 (і) = Х2 + 6X2 ехр (Я/), (8.46)

Причем | 6X1 К Хи | 6Х21 •С Х2. Пренебрегая членами, нелиней­ными относительно 6Х1( 6Х2, получаем

Характеристическое уравнение есть

]2 I k\k'zk2 -

А "Г k,2 - U, и Я, = fсо—мнимая величина. Частота колебаний равна

© = (8.48)

Таким образом, величины Xi и Х2 испытывают периодические колебания, амплитуды и фазы которых зависят от начальных условий. Фазы Х\ и Х2 разнятся. Для сравнения приведем рис. 8.11, на котором показана динамика популяций зайцев и ры­сей в Канаде за 1845—1935 гг. [27].

Посмотрим, выполняется ли термодинамическое условие ста­бильности в системе (8.40). Трактуя Х\ и Х2 как концентрации химических соединений, a k\, k2, k, k' как константы скоростей, имеем, варьируя для первой реакции Х\,

Bvx = kxbXx-kX\bXx,

2

Для второй реакции Х2

6v2 = k'X'l 6Х2 - k2 ЬХ2,

Лі

Причем = X\ = ki[k. Находим

"I" ~ hllf)(6X,)J + {k2lf~ = (8-49)

Т. е. условие устойчивости выполнено.

Мы исследовали поведение консервативной системы. В дей­ствительности популяции видов могут расти лишь до некото­рого предела, до значений Х[т) и Х2т\ отвечающих насыще­нию. Это обстоятельство можно выразить уравнением Фер - хулста [107] (см. также [26, 108])

X = kX{X^-X) . (8.50)

Вводя предел размножения жертв в уравнения Вольтерра, по­лучаем

^ {х[т) - Xt) - kX, X2, }

Ї (8.51)

Х2 == kf Х\Х2 — k2X2. )

Такая система более не является консервативной и не имеет постоянной движения.

Уравнения типа (8.40) можно обобщить на любое число взаи­модействующих видов. Исследование соответствующих систем очень важно для экологии (см. [26]<).

То обстоятельство, что постоянная движения консервативной системы К выражается суммой индивидуальных членов, относя­щихся к отдельным видам, позволяет трактовать систему как статистическую. Такая трактовка для ансамбля большого числа

Видов, взаимодействие которых описывается уравнениями Воль­терра, была предложена Кернером [109]. Вернемся к химическим реакциям.

Рассмотрим теперь поведение системы в промежуточной об­ласти конечных, но больших значений полного сродства 1 <С <С S4-/RT < оо. Представим систему реакций Лотка в несколько изме­ненном виде [1]

А + Хф+2Х,

K-i

X + YJ=*2Y, yJ^E.

Положим 4 = 1 и для простоты примем ki = — kz = 1 и k-\ — — k-2 = k-3 = k. Здесь мы уже не можем пренебречь обратными реак­циями. Имеем

X = X + kX2 - XY + kY\ 1

\ (8.52) Y = XY + kY2~Y + kE, J

И стационарные решения удовлетворяют уравнениям

Хй = 1 + kYa - kE/Y0, т* - f (1 - k + 2k2) r30 + (k - 1 - kE - 2k3E) Y2 +

+ (kE-2k2E)Y0 + k3E2 = 0. (8.53)

На рис. 8.12 показаны эти решения как функции полного срод­ства зФ для k = Ю-2 [1]. Характеристическое уравнение имеет вид

А2 + (У0 - Х0 + 2kX0 + 2kY0) Х + Х0 + 2кХй -

- 1 - 2kXl - 2kY0 + Yu + 4k2X0Y0 = 0. (8.54)

При всех значениях общего сродства вещественная часть X от­рицательна. Следовательно, термодинамическая ветвь устойчива и флуктуации затухают. При А > 9,2 RT величина X становится комплексной и возникают колебания. При k = 0, Х0 = Y0 = 1, имеем X = і (см. также [28]).

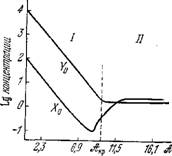
Рис. 8.12. Кривые зависимостей стационарных концентраций Х0 и Y0 от полного сродства в ло­гарифмическом масштабе.

] — область монотонного поведения // — область колебаний.

Обратимся к исследованию химических нестабильностей. Ясно, что они возникакт при наличии автокаталитических стадий (см. стр. 76). Рассмотрим систему химических реакций
несколько более сложную, чем система Лотка — Вольтерра:

(I)

2X + YJ^3X, (И)

K-2

B + xJ^D + Y, (III)

-з

| (8.55)

Х^±Е. (IV)

Суммарная реакция есть А + В D -)- Е. Условия равновесия имеют вид

Положим для простоты k\ = ki = k3 = k4 = 1 и k-\ = = = fe-з = ft-4 = 0. Кинетические уравнения записываются следующим образом:

X = А + X2Y - ВХ — X + k (DY + Е — X - X3),

Y = BX — X2Y + k (X3 - DY).

Стационарные решения имеют вид

A + kE k)& +В

Х0 = — , Yq = У Ха. 8.56)

0 1 + k х2 +в '

Реакции (I) и (IV) на устойчивость системы не влияют. По­этому можно упростить выражения (8.56), считая, что А и Е находятся в равновесии, т. е. А = k2E. Получаем

У —А v — А И2 + кВ) ,я А2 + к* В ■

Ищем решения линеаризованных уравнений вблизи стационар­ного состояния и находим характеристическое уравнение (ср. стр. 415)

Tf + lxl + B + l-2X0Y0 + k(3Xl + D+\)~]X +

+ ХІ+ k(X20 + D) = 0. (8.58)

Значение BID, при котором коэффициент при X обращается в нуль, отвечает точке перехода. В ней вещественные части кор­ней Яі и \2 меняют знак, и система становится неустойчивой.

Имеем Ул + = 0, и условие перехода на основании (8.57) и (8.58) имеет вид

Якр = ("§-)кр =

Соответствующее критическое сродство равно

SЈKp = - RT In RKpk2.

Зависимость критического сродства от D (при А = казана на рис. 8.13. Из (8.59) сле­дует, что Rtф >0, если 0 < D < < A2/k3. При D = 0 или беско­нечности S& КР стремится К ОО, для значения Рт 1л сродство имеет минимум. Стационарные состояния устойчивы и лежат на термоди­намической ветви для значений s4- < st>Кр.

X. 1

J (8.61)

Причем

Упростим задачу. Положим k = = 0; тогда кинетические уравнения (8.55) примут форму

X = A + X2Y-BX' Y — ВХ — X2Y.

Уравнение (8.58) превратится в уравнение

+ + 1 -2X0Y0)X + Xl = 0, (8.62)

Х0 = Л, У0 = В/А. (8.63)

Система становится неустойчивой при переходе через значе­ние В, удовлетворяющее условию

ХІ+В+ 1 -2XqY0 = A2+ В+ 1 — 26 = 0,

Т. е. при

1) по-

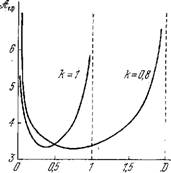
Рис. 8.13. Зависимость крити­ческого сродства от D.

В>Вкр=\ + А2. (8.64)

Х + А

Исключая У и У из (8.61) и положив X(t) = A + x(t), получаем нелинейное уравнение для х:

[х3 + ЗЛл-2 + (ЗЛ2 - В - \)х + А(А2 - В + 1) - 2х] х +

+ х(х + Л)2 = 0. (8.65)

14 М. В. Волькенштейн

Теория показывает, что при

А2 — В + 1 <0

Последнее уравнение имеет периодическое решение. Но ЭТО и есть условие неустойчивости (8.64). За точкой перехода периоди­ческие решения всегда находятся на конечном расстоянии от стационарного состояния.

Точка перехода есть точка бифуркации (см. стр. 404), опи­сываемая схемой

Устойчивы^ предель - Устойчивый Центр (в линейном приближении); S Ный цикл фокус негрубое образование V гг „ „ ,

4 Неустойчивый фокус.

Для области за точкой бифуркации численные расчеты фазо­вых траекторий, отвечающих системе (8.61) при различных на­чальных значениях X, Y, проведены в работе [29]. Результаты расчетов показаны на рис. 8.14. Неустойчи­вый фокус (он показан крестиком) находится при X— 1, У = 3. Пре­дельный цикл, представляющий не­затухающие колебания, возникает независимо от начальных условий и является устойчивым и единствен­ным. В отличие от системы Лот­ка— Вольтерра, имеющей беско­нечное число возможных периодиче­ских движений, система (8.55) или (8.61) характеризуется когерент­ным поведением и не является кон­сервативной. Это автоколебатель­ная система, которую можно на­звать «химическими часами» (см. § 8.5). Дальнейшие подроб­ности см. в работах [1, 2].

Рассмотренные нелинейные химические системы обнаружи­вают поведение, упорядоченное во времени, —• периодические ко­лебания.