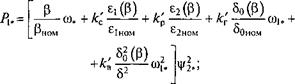ЭНЕРГОСБЕРЕГАЮЩИЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД
Мощность потерь в системах ППЧ — АД при типовых законах частотного управления
При частотном способе регулирования скорости асинхронных электродвигателей, как отмечалось выше, необходимо изменять не только частоту, но и амплитуду питающего напряжения. От соотношения частоты и амплитуды зависят механические характеристики и энергетические показатели электропривода, поэтому с практической точки зрения важно знать механические и энергетические характеристики асинхронного электропривода при различных законах частотного управления в условиях изменения скорости и момента нагрузки.
При регулировании скорости АД ниже номинальной широко распространены следующие законы управления:
закон пропорционального управления и,/со, = const; управления при постоянстве потокосцепления обмотки статора ej/co! = i|/i = const;
управления при постоянстве главного потокосцепления е0/(о{ = |/0 = const;
управления при постоянстве потокосцепления обмотки ротора e2/(tii =j/2 = const, где Щ, Є, е0 и е2 — модули векторов напряжения статора и ЭДС, наведенных потоками статора, главным потоком и потоком ротора; |/ь ц/0 и |/2 — модули векторов полных потокосцеплений обмотки статора, главных и полных потокосцеплений обмотки ротора.
В первом приближении расчет механических и энергетических характеристик привода можно производить, пренебрегая насыщением магнитной цепи АД. В этом случае удается получить сравнительно простые аналитические выражения и процедуры расчета характеристик при перечисленных законах управления. Однако при учете нелинейности кривой намагничивания для получения более точного расчета в ряде случаев, например при законах управления Wi/cdj = const и = const, расчет механических и энергетических характеристик существенно усложняется. Это вызвано необходимостью определения магнитного состояния АД (координат точки кривой намагничивания машины), что связано с применением итерационных процедур решения нелинейных систем алгебраических уравнений.
Исходные характеристики установившегося режима асинхронного двигателя. Примем в дифференциальных уравнениях (2.27)... (2.31) математической модели системы ПЧ—АД оператор дифференцирования р = d/cit, равным нулю. В результате будем иметь уравнения, описывающие установившийся режим работы системы. Дальнейшее преобразование этих уравнений позволяет получить ряд полезных характеристик асинхронного электропривода при частотном способе регулирования скорости двигателя.
Исходные характеристики АД запишем в частично относительной системе единиц, представив их в виде зависимостей модулей результирующих векторов напряжения И,,= щ/щнои, ТОКОВ /}, = ij/ijном, потокосцеплений |/у, = |/у/|/уном и ЗЛЄКТрОМаГНИТНОГО момента Мщ = = М/МНом двигателя ОТ скорости (О, = C0/(w1hom/Ai)3 абсолютного скольжения (3 = (сої — со3)/а)іном и модуля результирующего вектора полных потокосцеплений обмотки ротора |/2*. Напомним, что Ю] = 2тг/ь а
^ІНОМ = 2Tif ном-
Относительная угловая частота напряжения и тока статора
(Oj* = со* + |3. (3.5)
Напряжение, ток и полное потокосцепление обмотки статора в относительных единицах находятся по формулам:
2 Cl 2 х-5 г
щ*=—р - щ*, (3-6)
Ыном
|
Єї |
/2 =£!ІР)¥2>; (3-7)
НОМ
,2 _5'(0Ь
vf.=^v!.. (3.8)
*^1ном
Результирующий ток намагничивания и главное потокосцепление в относительных единицах определяются по формулам:
&=—Ч&; (3.9)
^Оном 9 5о (р) ,
Vo*=X"^¥2*- (3.10)
ООном
Ток обмотки ротора в относительных единицах рассчитывается по формуле
/22*=^-®V2*. (ЗЛ1)
^2ном
Электромагнитный момент в относительных единицах находится по формуле
М’=-Г - vI - (3.12)
Рном
В формулы (3.6)...(3.11) входят функции, которые зависят от частоты вращения и абсолютного скольжения или только от абсолютного скольжения и рассчитываются по следующим формулам:
Сі (ю„р) = 2Й, (со, +Р)РЛ2-' + [б2 +с2(о>. +р)2]р2Л2-2 +
+d1 + е2 (<в, +Р)1 ; £,(Р) = V + ^2(i + ^0'%o)2P2;
to(P) = V(i+^A!); (ЗЛЗ)
є2 (р) = Я2~2р2;
81 (р) = е2 + R22c2$2; бо (р) = і + /г22х2стр2.
Коэффициенты b, с, d, e определяются по значениям параметров Т-образной схемы замещения АД при переменной частоте [53]:
Ъ = ЗД + Х2аХ-0') с = Х1а + Х2а + адДо1;
d=R, Xt, е=1+Х1аХъ
где индуктивные сопротивления Xla = L]a(0lHOM; Х2а = I2aco, HOM; XQ =
= ZqCO|hom.
При учете насыщения двигателя по главному магнитному пути изменяется индуктивное сопротивление Х0 = Lowihom - Характеристика намагничивания представляется нелинейной функцией вида
Уо* = Уо*0'о*) или /0» = /о*(і|/о*).
При этом связь между величинами і|/0*, /о* и Х0 устанавливается формулой Х0 = Х0номщ*/і0*.
В выражения (3.6)...(3.11) входят константы, которые определяются с помощью формулы (3.13) при подстановке номинальных значений со* = соном» и 3 = рном. Тогда
Сіном = Cl(^ ном*? Рном)з ^НОМ “ ЄіО ном) 5 ^Оном “ Чф НОм) з
^2ном = ^2(Рном)з ^Іном = ^1 (Рном)з ^Оном = ^о(Рном)*
Энергетические характеристики АД (активную Ри, реактивную (),*, полную S{*, механическую Рмех, МОЩНОСТИ И COSCpflB) можно также представить функциями от скорости со*, абсолютного скольжения Р и модуля результирующего вектора полных потокосцеплений обмотки ротора ц/2*. При выборе в качестве базисной величины электромагнитной мощности двигателя в номинальном
режиме энергетические характеристики АД записываются в следующем виде:
|
|
|
Оном |
(3.14)

|
(3.15) |
|
>ном |
|
|
|
cos фдв =Pi*S{};
'ном 'ном |
(3.16)
(3.17)
(3.18)
В формулах (3.14)...(3.18) постоянные коэффициенты к'с =
_ А^ім. ном/Дм. ном) кр ~ А^м. ном/^эм. номэ — ^Рс. г.ном/Дм. HOM5 ~
= АЛс. в ном/Дм. ном характеризуют удельный вес составляющих полных потерь по отношению к электромагнитной мощности двигателя при работе в номинальном режиме.
Номинальный параметр машины, определяемый как отношение полной мощности к электромагнитной мощности двигателя в номинальном режиме [63], определяется по формуле
|
|
|
ном |
К особенностям приведенных выше исходных характеристик электропривода относятся следующие. В качестве независимых внешних переменных наряду со скоростью двигателя со* и абсолютным скольжением (3 принимается полное потокосцепление ротора у2*. Выбор со*, (З, |/2* в качестве независимых величин при расчете характеристик позволяет исключить в цифровых алгоритмах деление на 0 при значении р = 0. В некоторых случаях для достижения этой цели вводится вспомогательная переменная [63]. Кроме того, сочетание со,, р, |/2* дает возможность в ряде случаев более эффективно решать задачи синтеза законов управления, оптимизирующих режимы работы частотно-регулируемого асинхронного электропривода. Наконец, используемый вариант системы относительных единиц позволяет оценить исследуемые режимы
двигателя по отношению к его характеристикам в номинальном режиме.
Закон пропорционального управления. При этом законе управления амплитуда напряжения, прикладываемого к обмотке статора, изменяется пропорционально частоте со^ Закон пропорционального управления является самым простым из известных законов частотного управления. На практике используется зависимость
и, =кт ь
где и1ном и (о1ном — значения амплитуды и угловой частоты напряжения в номинальном режиме асинхронного двигателя.
Основные соотношения в режиме пропорционального управления получим, воспользовавшись исходными характеристиками АД. В случае пренебрежения нелинейностью кривой намагничивания двигателя расчет его механических характеристик при законе пропорционального управления сводится к следующей процедуре. При фиксированной частоте о»!*, задавая шаг Дсо* для ряда значений угловой скорости со*, рассчитываются напряжение их„ параметр абсолютного скольжения 0 и электромагнитный момент М* асинхронного двигателя. Расчеты целесообразно производить по следующим формулам:
|
«!* = &&>!*; (3 = со і * — со*;
|
(3.19)
(3.20)
(3.21)
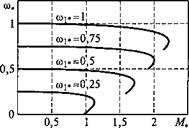
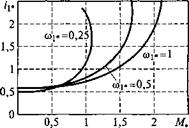
По данным расчетов строится зависимость Л/*(со*) для заданной фиксированной частоты «!*. Задаваясь рядом значений фиксированных частот coj*, получим семейство механических характеристик двигателя при данном законе управления. На рис. 3.4 показаны рабочие характеристики АД при законе пропорционального управления.
На рис. 3.4, а изображено семейство механических характеристик АД типа 4А132М6, имеющего Рнои = 7,5 кВт, при фиксированных частотах.
Приведенные графики механических характеристик показывают, что при изменении Mj* согласно формуле (3.19) в диапазоне частот 0,5 < coj* < 1 критический момент и критическое скольжение двигателя незначительно отличаются от их значений при номинальной частоте.
|
|
|
«і- |
|
При дальнейшем уменьшении частоты со!* механические характеристики заметно ухудшаются, критический момент существенно уменьшается, а критическое скольжение увеличивается. Значения координат характерных точек механических характеристик можно рассчитать по известным аналитическим выражениям. Так, в случае пренебрежения эффектами насыщения магнитной цепи и вытеснения тока в роторе координаты критических точек механических характеристик в режиме пропорционального управления определяются по следующим формулам: |
|
Рис. 3.4. Рабочие характеристики АД: механические (а) и напряжения статора (б) при законе пропорционального управления |
|
id2 + е |
|
Ь2 + с |
|
В которых константа Сном = 2Л, + (Ь2 + с2 )|3Н0М R21 + (d2 + е2)рн'м R2. При оценке момента короткого замыкания АД, когда со* = 0, Р = со!*, в случае пренебрежения эффектом насыщения магнитной цепи и вытеснением тока в роторе можно пользоваться выражением М = Г _________________________ ^ Ю|*___________________ кл* Shom 2Д, со2* + (b2 + с2со2*)R2lсо2* + (d2 + e2co2*)R2' Известно, что причиной ухудшения механических характеристик АД при уменьшении частоты является снижение магнитного потока, что обусловлено падением напряжения в активных сопротивлениях Л, обмотки статора (см. рис. 1.1). На рис. 3.5 приведе- |
|
Я, СО,* ± b2 + c2cof* ){d2 + £2С02* ) |
|
к2 со2* |
|
а>1»=0',75 |
|
coi*=0,5 |
|
0,5 |
|
Ш]*=0,25 |
|
0 |
|
Л/. |
|
0,5 |
|
1,5 |
|
1 |
|
2(0к |
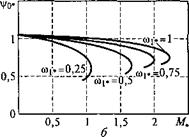
ны зависимости тока намагничивания и главного потокосцепле - ния двигателя от М», соответствующие семейству механических характеристик в режиме управления щ = кщ. Эти характеристики, если не учитывать насыщение двигателя, могут быть рассчитаны по следующим формулам:
Vo. = to, Js'H°M г trW (3-22)
у^Оном Cl (®1*jP)
(3.23)
|
|
|
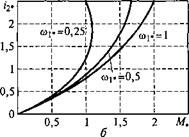
Рис. 3.6. Электромеханические характеристики изменения токов статора (а) и ротора (б) АД при законе пропорционального управления |
Как следует из формул (3.22) и (3.23), результирующий ток намагничивания и соответствующее этому току главное потоко - сцепление уменьшаются с уменьшением частоты питающего напряжения. Снижение этих величин проявляется особенно заметно в области низких частот. Вместе с тем изменение момента оказывает влияние на намагничивающий ток и главное потокосцепление,
|
|
|
Рис. 3.5. Зависимости тока намагничивания (а) и главного пото - косцепления двигателя (б) от М, при законе пропорционального управления |
которые увеличиваются по мере того, как увеличивается момент двигателя.
Рассмотрим энергетику привода в режиме пропорционального управления. При расчете суммарных потерь в двигателе АРдв необходимо знать согласно формуле (2.42) главное потокосцепление j/0, ток статора і і и ток ротора /2 АД при законе пропорционального управления. Для линейной магнитной цепи двигателя главное потокосцепление |/0 определяется по формуле (3.22). Для расчета токов обмоток статора /] и ротора /2 можно воспользоваться следующими формулами:
Формулы (3.24) и (3.25) можно также использовать для расчета токов статора и ротора в режимах идеального холостого хода и короткого замыкания, подставляя в первом случае со. = со^, Р = О, а во втором — со* = О, (3 = coj*. Ток статора в режиме идеального холостого хода определяется при законе пропорционального управления выражением
*Чном /?2 + -^1а ) СО
а ток короткого замыкания — выражением
|
Ак. з* — ^СО, |
С,„„и R?(b>RM,+d>R2)
є1ном 2^caf, + (b2 + c2co2*)R2 ‘cof, + (<d2 + e2cof*) R2
Характер изменения токов статора /ь ротора /2 и главного по - токосцепления |/0 позволяет оценить тенденцию изменения составляющих суммарных потерь в двигателе и системе ПЧ—АД.
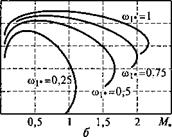
На рис. 3.6 показаны электромеханические характеристики изменения токов статора и ротора АД при законе пропорционального управления. Как видно на рис. 3.6, в диапазоне частот 0,5 < coj*< 1 при изменении момента от нуля до номинального значения токи статора и ротора мало зависят от частоты. В этом случае основное влияние на токи статора и ротора оказывает изменение момента нагрузки. Однако при дальнейшем снижении частоты все больше
проявляется тенденция к увеличению токов в обмотках двигателя, что особенно заметно при значениях момента, превышающих номинальное значение. Следствием этого является увеличение потерь в меди обмоток статора и ротора при уменьшении частоты напряжения в режиме пропорционального управления. Увеличение тока статора приводит также к увеличению добавочных потерь, пропорциональных квадрату тока статора. Что касается потерь в стали и механических потерь, то эти составляющие суммарных потерь в режиме пропорционального управления по мере снижения частоты уменьшаются.
Для определения суммарных потерь в двигателе значения токов и потокосцепления, рассчитанные по формулам (3.22), (3.24) и (3.25), нужно подставить в выражение суммарных потерь в двигателе (2.42), предварительно записав его в относительных единицах, т. е.
Л/U = (кс + кд)/J + kpil + (кт + квcoj*)co1#j/g* + кмехоуЦ2. (3.26)
Постоянные коэффициенты, характеризующие удельный вес составляющих суммарных потерь по отношению к мощности потерь в номинальном режиме, определяются по следующим формулам:
/ _ Д^ІМ. НОМ. / _ Д-^2м. ном. / _ Д^їс. Г.НОМ.
с " АР ’ р " АР т~ АР
дв. ном LXA дв. ном дв. ном
АР АР АР
1. _ ІС. В.НОМ. 1Г _ доп. ном. / _ *-»-* мех. ном
в " АР ’ АР ’ мех ~ АР
ДВ. НОМ LS1 ДВ. НОМ 1Л1 ДВ. НОМ
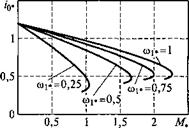
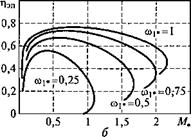
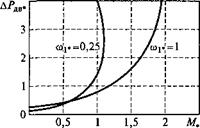
На рис. 3.7 показаны энергетические характеристики суммарных потерь и КПД АД типа 4А132М6 при фиксированных частотах. Анализ кривых (см. рис. 3.7) показывает, что при номинальном моменте потери в двигателе практически равны номинальным потерям при изменении частоты в диапазоне 0,5 < о>|* < 1. При том же моменте уменьшение частоты приводит к увеличению суммарных потерь по сравнению с номинальными. Так, при (Oj* = 0,25 суммарные потери в двигателе превышают величину его потерь при номинальном режиме работы на 20 %.
Потери в двигателе зависят как от частоты, так и от момента нагрузки. При невысоких нагрузках суммарные потери в двигателе с уменьшением частоты уменьшаются. Однако при перегрузках (М* >1) характер поведения суммарных потерь в двигателе меняется. В этих случаях с уменьшением частоты суммарные потери в двигателе начинают увеличиваться за счет увеличения потерь в меди обмоток статора и ротора, при том что потери в стали и механические потери уменьшаются. Так, при о»!* = 0,25 и перегрузке двигателя всего на 10 % суммарные потери в нем увеличиваются в 2 раза.
|
Рис. 3.7. Энергетические характеристики суммарных потерь (а) и КПД (б) АД типа 4А132М6 при законе пропорционального управления |
|
Рис. 3.8. Энергетические характеристики суммарных потерь (а) и КПД (б) системы ПЧ—АД при законе пропорционального управления |
|
|
|
|
а а
Пдв 0,8 0,6 0,4 0,2 0

Коэффициент полезного действия двигателя в режиме пропорционального управления также существенно зависит не только от частоты, но и от момента нагрузки. В исследуемом диапазоне частот 0,25... 1 максимальное значение КПД приходится на точку, характеризующуюся величиной момента М„, примерно равного 0,5.
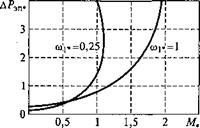
Проанализируем суммарные потери в системе ПЧ—АД и ее КПД, энергетические характеристики которой при законе пропорционального управления приведены на рис. 3.8. Характер поведения зависимостей потерь и КПД системы ПЧ — АД от частоты и момента в целом такой же, как в АД. Объясняется это тем, что основную долю потерь в системе составляют потери в двигателе. Однако за счет потерь в преобразователе частоты потери в системе ПЧ—АД увеличиваются, а ее КПД уменьшается.
Заметим, что входящее в формулы расчета характеристик индуктивное сопротивление Х0 считалось постоянной величиной, равной его значению при номинальном режиме работы АД (Х0 = Х0ном).
Правомочность практического использования приведенных ранее выражений для расчета характеристик при Х0 = ЛГ0ном может быть оценена по методике [63], которая сводится к анализу числен
ных значений главного потокосцепления |/0* и определения по ним рабочего участка реальной характеристики намагничивания.
В том случае, когда значения |/0* соответствуют нелинейному участку характеристики намагничивания и оценка по |/0* не удовлетворяет точности, расчет механических и энергетических характеристик производят с учетом насыщения машины. Рабочая точка на нелинейной характеристике намагничивания, соответствующая фиксированным значениям со^ и со*, определяется решением следующих нелинейных уравнений:
СіномМРК* -§0„омСі К, Р)|/о* = 0; (3.27)
«!* = A:coj*; (3 = coj* - со*; (3.28)
*0 = *0„ом%; (3.29)
/о*
h* = *о* (Vo*)* (3.30)
Совместное решение этих уравнений при фиксированных значениях coj* и со* дает потокосцепление j/0*.
Для решения уравнений (3.27)... (3.30) можно воспользоваться рекуррентными методами, разработанными для вычисления корней. При использовании метода касательных уравнение (3.27) приводится к виду
У^(^0*) = Сіном^О (Р)Ц* — ^ОномСі
Тогда итерационная формула метода касательных будет выглядеть так:
где X — коэффициент укорочения шага приближения, способствующий улучшению условий сходимости решения, А, < 1; Ґ(Щ*п)~ производная функции /(|/0*„) по переменной j/0*; п — номер итерации.
Для определения производной можно воспользоваться
точечной оценкой по формуле
/'(VO.») =^[/(Vo. + s)-/(Vo.-s)].
где g — достаточно малая величина, называемая базой оценки, т. е. расстояние между двумя значениями функции, g > 0.
Искомыми данной задачи являются |/0*, /0* и Х0. Зная (3, |/0* и Х0, нетрудно определить электромагнитный момент, токи и потокосцепления обмоток статора и ротора, а также рассчитать ряд других рабочих характеристик АД, ПЧ и в целом системы ПЧ—АД.
Вначале по формулам (3.29) и (3.30) определяется Х0. Затем
после определения коэффициентов a, b, end рассчитывается функ-
А/
ция/(уо*) и оценка ее производной/ (|/о*)- Далее рассчитывается приращение Л|/0*, которое сравнивается с заданной величиной погрешности вычисления корня ц/о*. Если выполняется условие Л|/0* < 0, то это свидетельствует о том, что корень найден. В противном случае производится новое определение потокосцепления J/0„, с которым проводится очередной цикл вычислений.
Таким образом, использование закона пропорционального управления Wj/cl»! = const для электропривода в области низких частот, а также для электропривода с глубоким регулированием скорости неэффективно. В этих случаях применяют специальные режимы управления с использованием средств автоматического регулирования или корректируют закон пропорционального управления, обеспечивая увеличение отношения их/Wj при понижении частоты СО] для частичной или полной компенсации падения напряжения на активных сопротивлениях обмотки статора.
Так, в промышленных электроприводах предусматривается следующая коррекция зависимости в области низких частот:
ихнт+кхщ при со, < со1гр; щ =
[к2щ при о, > со1гр,
где и1нач — значение напряжения при со, = 0; со1гр — граничное значение частоты, при которой происходит излом характеристики; кх, к2 — постоянные коэффициенты.