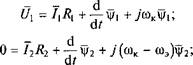ЭНЕРГОСБЕРЕГАЮЩИЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ И МОДЕЛИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ В УСТАНОВИВШИХСЯ И ПЕРЕХОДНЫХ РЕЖИМАХ
Располагая математическим описанием процессов работы асинхронного двигателя в статическом и динамическом режимах, можно получить временные зависимости токов статора и ротора, определить потери в асинхронной машине, проанализировать возможности их снижения при использовании энергосберегающих алгоритмов управления электроприводом в переходных и установившихся режимах и выбрать рациональные по электропотреблению способы и законы управления асинхронными двигателями.
Для математического описания процессов в асинхронной машине обычно используются дифференциальные уравнения обобщенной двухфазной машины переменного тока [32, 33, 71], полученные при общепринятых допущениях (без учета потерь в стали, высших гармоник магнитного поля при равномерном воздушном зазоре и напряжении питания, являющимися симметричной системой синусоидальных напряжений). Предполагается также, что параметры роторной цепи приведены к статорному контуру.
Исходные уравнения, записанные с использованием обобщенных пространственных векторов в системе координат, вращающихся с произвольной скоростью шк (при отсутствии внешних источников напряжения в роторных цепях) имеют вид:
|
|
(1.3)
|
|
(1.4)
|
(1.5) |
где Uх — обобщенный вектор напряжения статора; /ь /2 — обобщенные векторы тока соответственно статора, ротора; RUR2 — активное сопротивление обмотки соответственно статора, ротора; ргь j/2 — обобщенные векторы потокосцепления соответственно статора, ротора; сок — электрическая угловая скорость вращения координатных осей; соэ — электрическая угловая скорость вращения ротора,
о)э= ті,
где ш — механическая угловая скорость ротора; М — электромагнитный момент, развиваемый двигателем; рп — число пар полюсов асинхронной машины; L0 — индуктивность намагничивающего контура; Jm — знак, указывающий на то, что берется только вещественная часть комплекса.
|
|
Для исследования переходных процессов система уравнений
(1.3) и уравнение (1.4) дополняются уравнением движения электропривода:
(1.6)
где Мс — момент статической нагрузки; J — приведенный к валу суммарный момент инерции электропривода, /= /дв + /мех; /дв и /Мех— момент инерции двигателя и приведенный к валу двигателя момент инерции механизма.
Система уравнений (1.3), записанная через проекции обобщенных векторов на ортогональные оси и, jv координатной плоскости, вращающейся с произвольной скоростью сок, имеет следующий вид:
Щи ~ Rhu PWu
|
(1.7) |
uv = Rhv +а)к¥іиі
О = R2i2u + p|/2« - (сок -(o3)|/2t,; 0 = R2i2v +PV2v+ (а>к ~ <*>э)Х|/2«,
где p — оператор дифференцирования.
В этом случае электромагнитный момент, развиваемый асинхронным двигателем, может быть определен из выражения
|
(1.8) |
М - — Рп^о (huhv ~ huhv)-
Рациональное значение сок зависит от типа решаемой задачи и, как правило, принимает одно из следующих значений: шк = О (в этом случае принято обозначать координатные оси а, у'Р); сок = = (о0э (координатные оси х, jy) сок = соэ (координатные оси d, jq). Здесь со0э — электрическая угловая скорость электромагнитного поля статора. Эта величина соответствует электрической скорости холостого хода. Заметим, что механическая угловая скорость холостого хода, она же — синхронная скорость, со0 = щэ/рп.
Отметим, что, обозначая угловую скорость через со и измеряя ее с-1, зачастую определение «угловая» опускают и оперируют термином «скорость».
Связь между полным потокосцеплением статора j/b ротора j/2, главным потокосцеплением j/0 и токами статора ix и ротора /2 ненасыщенной асинхронной машины выражается следующим образом:
|
(1.9) |
¥і - Ls! + LqIj', ¥2 = Lrl2 + LqIu
где Ls= L0 + LXa — полная индуктивность обмотки статора; Z, lcr — индуктивность рассеяния обмотки статора; Lr= L0 + L2a — полная индуктивность обмотки ротора; Ь2а — индуктивность рассеяния обмотки ротора. _
Если учесть, что /0 = І + І2, то выражения (1.9) можно записать в следующем виде:
|
(1.10) |
¥1 - Lah + ¥<ъ ¥2 = blah + ¥05
где щ = LqIq, LXaIi =|f]a; Ь2аІ2=Щв ¥іо, ¥20 — потокосцепления рассеяния соответственно статора, ротора.
Запишем выражения для потокосцеплений через проекции на оси комплексной плоскости:
|
(1.11) |
¥iw ¥o« ohm ¥ь = ¥(b + Iao4v ¥2и = ¥o« + J-Q. Ju
¥2у = ¥0t) + J-Q. ahv
¥ои —
¥(b - Loiov
При необходимости учета насыщения целесообразно использовать следующую систему уравнений:
щ =|/0 +Vi„;
¥2 =¥0 +?20;
|
(1.12) |
Vo = А) (|А)|)Лъ 70 - 7j + 72; ¥іст - - А О A 5 ¥2а = Llall-
В системе уравнений (1.12) переменная индуктивность L0(J01), с помощью которой учитывается насыщение двигателя по главному магнитному пути, рассчитывается по кривой намагничивания:
Г. П/П ¥°(17°1)
где ¥о(|^о|) — нелинейная функция (характеристика намагничивания, определяющая связь между модулем |j/0| результирующего вектора главных потокосцеплений vj/0 и модулем |/01 результирующего вектора намагничивающих токов /0).
В ряде случаев для вычисления индуктивности удобно использовать выражение
kflffi п (N)
м) V ¥о / т /|_ | 5
(|Vo|)
где /0(|¥о|) — обратная по отношению |/0(|701) нелинейная функция.
Приведенные уравнения могут быть использованы для анализа как переходных (в этом случае система уравнений асинхронной машины является нелинейной и может быть решена численными методами с использованием ЭВМ), так и установившихся режимов.
Для анализа установившихся режимов при переменной частоте питающего напряжения (/, * const) примем в системе уравнений (1.3) скорость сок = о)0э = 2nfb производные примем равными нулю, тогда получим следующую модель, описывающую установившийся режим работы двигателя:
U = усад/і + Rh
0 = У(03Оэ -W3)¥2 +^2^2;
j7, =j/0 + via;
V2 = Vo + V2C;
|
(1.13) |
Vo = A) (|/o|)/o; i0 = ix + /2;
Via = AaAi V2a = LlcJl,
M = |д, Im[j/0x/i];
M = MC.
На основании уравнений установившегося режима построим схему замещения асинхронного двигателя при переменном значении /. Для этого в уравнениях электрического равновесия напряжений исключим результирующие векторы полных потокосцеп - лений обмоток статора. vj/ х и ротора j/ 2. В полученных уравнениях выразим результирующие векторы главных потокосцеплений j/0 и потокосцеплений рассеяния обмоток статора vj/la и ротора Ц/2о через результирующие токи соответственно 70, Iх и 72. После несложных преобразований получим уравнения следующего вида:
|
(1.14) |
U = RXJX + j(Oo3LaIx + ушоэ А)Ль
R? - -
О = ^2 + 7<*>0э^2а^2 + .М)эА)Ль
|
|
|
— скольжение; со0 = |
|
Wq СОдэ |
—; 03ОЭ = 2 л/,.
Ра
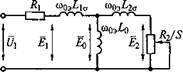
Системе уравнений (1.14) соответствует схема замещения асинхронного двигателя при переменной частоте питающего напряжения, приведенная на рис. 1.1.
В схеме замещения учтено насыщение асинхронного двигателя с помощью переменного коэффициента L0, являющегося функцией тока намагничивания |/0|.
Наведенные в электромагнитных контурах ЭДС можно записать следующим образом:
Е = Усо0э? ь
Ёо = У<ооэ? о; Ё2 = М)э?2-
Схема замещения, приведенная на рис. 1.1, может использоваться для анализа установившихся режимов асинхронного двигателя при частотном способе регулирования угловой скорости.
В системах асинхронных электроприводов с регулированием напряжения первой гармоники переменного напряжения или добавочного сопротивления в роторе частота питающего напряжения остается постоянной и равной номинальному значению, т. е. fl = ~ / ном и со0э = Ыоэ. ном = 2те/1ном. Для этих случаев уравнения статических режимов приобретают следующий вид:
U = IR + jIX + j'IqXo',
0 = T2R2 + j'IqXqS + jT2X'2S,
ГДЄ X — ОІОз-ном-^Іст 5 X2 — Wo3-Hom^-'2o? -^0 — ^Оэ. ном-^СЬ X, X2 ИНДУК - тивные сопротивления рассеяния обмоток соответственно статора, ротора; Х0 — индуктивное сопротивление контура намагничивания.
В уравнениях статических режимов (1.15) с помощью I2, R{, Х2 обозначены параметры ротора, приведенные к параметрам обмотки статора, а выражение IqXq представляет собой ЭДС контура намагничивания:
Ео=ЛоХо=Мэ. ноМ - (1-16)
С учетом (1.16) система уравнений (1.15) будет представлять собой систему уравнений статического режима работы асинхронного двигателя при /, = fH0M, которому соответствует Т-образная схема замещения (см. рис. 1.1).
|
Ri/S |
|
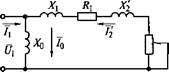
Рис. 1.2. Г-образная схема замещения асинхронного двигателя в статических режимах |
|
|
Часто для упрощения анализа статических режимов используют Г-образную схему замещения, для чего подключают контур намагничивания непосредственно к зажимам питающего напряжения, что не вносит существенных погрешностей в расчеты. Г-образная схема замещения асинхронного двигателя в статических режимах приведена на рис. 1.2. В такой схеме ток /0 = Ux/XQ
|
Рис. 1.1. Схема замещения асинхронного двигателя при переменной частоте питающего напряжения |
остается в процессе работы двигателя постоянным и не зависит от скорости (скольжения) двигателя.
|
|
Приведенные при /і = /і ном уравнения статических режимов (1.15) и схема замещения (см. рис. 1.2) могут быть использованы для исследования свойств и характеристик асинхронного электропривода как при регулировании напряжения Ub подводимого к статору, так и при регулировании добавочных сопротивлений ротора і?2доб. Это можно реализовать в асинхронных двигателях с контактными кольцами, для чего в схеме замещения вместо R2 нужно использовать значение R'2Z = R'2+ R2a06- Для двигателей с короткозамкнутым ротором R'2X = R'i- Тогда ток ротора
(1.17)
|
|
При известном токе ротора можно определить статорный ток:
(1.18)
где /1ном и 1'2ном — соответственно номинальный ток статора, приведенный номинальный ток ротора.
Выражение (1.18) может быть преобразовано следующим образом:
|
|
(1.19)
где Мном и 5ном — соответственно номинальный момент и скольжение двигателя.
Момент двигателя

|
|
|
3 U}R[, |
|
1 ^21 |
|
М = |
(1.20)
Называемый критическим максимальный момент двигателя
|
|
(1.21)
Критическое скольжение, соответствующее критическому моменту,
(1.22)
№+(X1+Xif
В формулах (1.21) и (1.22) знак «+» соответствует двигательному режиму работы двигателя, а знак «-» — тормозному. Используя формулы (1.21) и (1.22), можно получить уточненную формулу Клосса для записи зависимости момента асинхронного двигателя от скольжения:
2МК (1 + aSK) .. ...
М - —------------------- —— (123)
S/SK+SJS + 2aSK’
где а = R/R'21.
В ряде случаев используют упрощенную формулу Клосса, приняв а = 0. Тогда
2 М
М= ‘. (1.24)
S/SK + SK/S
При исследовании переходных режимов систему уравнений
(1.3) , формулы (1.4) и (1.5) записывают обычно в относительных единицах [63, 71, 76]. Рациональный выбор системы базовых единиц зависит от типа анализируемого асинхронного электропривода и исследуемых задач [63].
Приведенное математическое описание переходных и установившихся процессов в асинхронном двигателе показывает, что управляющими воздействиями, изменяющими характеристики двигателя, являются амплитуда (или действующее значение) переменного питающего напряжения, частота и амплитуда переменного напряжения, подводимого к статору, суммарное активное сопротивление роторных цепей (для двигателей с фазным ротором, когда можно изменять значение добавочного сопротивления ротора).
В современных системах электропривода регулирование указанных параметров производится с использованием различных типов полупроводниковых преобразователей, поэтому исходные выражения должны быть дополнены математическим описанием и моделями рассматриваемых типов преобразователей с учетом систем управления ими, что позволит анализировать процессы в системе «преобразователь — асинхронный двигатель». В зависимости от рассматриваемого класса регулируемых асинхронных электроприводов и исследуемых режимов анализ процессов может быть проведен с учетом полигармонического состава питающего напряжения при использовании полупроводниковых преобразователей или
только по гладкой (полезной) составляющей питающего напряжения, а также с учетом насыщения магнитной цепи асинхронной машины или при постоянстве параметров и др. Эти вопросы будут проанализированы в гл. 2.