Электронный Парамагнитный резонанс в биологии
Электронное расщепление в атомах переходной группы
Выше мы рассмотрели электронное расщепление в случае I риплетного состояния, обусловленного двумя неспаренными электронами, находящимися на делокализованной молекулярной чрбитали. Однако и единичный атом может обладать не одним, .1 несколькими неспаренными электронами; особенно это характерно для атомов переходной группы. В атомах 1-й переходной группы, например, сначала запо. лняется 4?-оболочка, а затем уже '«^-оболочка; следовательно, могут существовать такие атомы или ноны, где число электронов на Зй-оболочке варьирует от 1 до 10 и, таким образом, на данной атомной оболочке могут находиться до пяти неспаренных электронов. Действительно, существуют атомы железа и марганца с пятью неспаренными электронами на Зй-оболочке; все эти электроны могут быть ориентированы н одном направлении, и в этом случае полное электронное спиновое квантовое числю S = 6/2. Эти ионы представляют значительный интерес для биологических и биохимических исследований; ион железа играет важную роль в молекулах такого типа, как гемоглобин, а ионы марганца часто присутствуют в качестве примесей в водных растворах и, следовательно, их спектр необходимо отделять от спектров исследуемых веществ. Поэтому полезно рассмотреть частный случай электронной структуры этих двух атомов в качестве еще одной иллюстрации электронного расщепления в типичном спектре ЭПР:
Следует отметить, что у этих двух ионов (каждый из них характеризуется спектроскопическим состоянием 6S) полное электронное спиновое квантовое число S может быть равно 5/2 только при условии, что они связаны со своими ближайшими соседями ионной, а не сильной ковалентной связью. Далее будет показано, что такая сильная ковалентная связь может изменять число неспаренных электронов в ионах железа и марганца, но л ока мы предположим, что существует только связь ионного типа и что, следовательно, каждый из пяти электронов Зй-оболочки обладает собственной орбиталью, спины их ориентированы в одном направлении и S = ®/2. Спектроскопическое состояние 6S есть не что иное, как орбитальное синглетное состояние, не обладающее угловым моментом. Таким образом, в первом приближении можно считать, что в этом с. лучае магнитные моменты по. лностью обусловлены спином и, следовательно, значение ^-фактора также очень близко к 2,0.
|
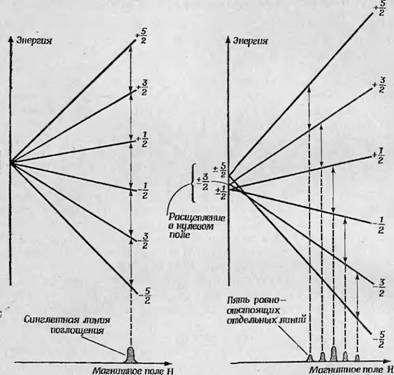
Фиг. 7. Электронное расщепление в спектре ЭПР иона Мп2+. А — расхождение энергетических уровней щщ наложении магнитного поля в отсутствие внутренних электрических полей; Б — расхождение подуровней, образующихся в результате расщепления в нулевом магнитном поле под действием внутренних полей, при наложении магнитного поля. |
|
А Б |
|
(фиг. 7, А). При наложении внешнего магнитного поля для спинов будут возможны только такие ориентации по отношению к этому полю, в которых их проекция Мs имеет значения +5/2 (в направлении поля), +3/2, +1/2", —г/2, —3/г и Этим различным ориентациям соответствует и разная энергия; таким образом, наложение внешнего магнитного поля вызывает расщепление энергетических уровней (фиг. 7, А). Переходы из одного состоя- |
У свободных ионов железа или марганца, не подвергающихся действию внутрикристаллических или молекулярных электростатических полей, различным ориентациям полного спинового вектора с квантовым числом S = 5/2 соответствует одна и та же - энергия и, следовательно, все энергетические уровни вырождены
пин в другое, как и всегда, подчиняются обычному квантовому правилу отбора Ms = ±1, откуда следует, что разрешены только' переходы, обозначенные стрелками; очевидно, что для данной микроволновой частоты все возможные переходы будут иметь место при одном и том же значении внешнего магнитного поля и, следовательно, так же, как и в случае трех уровней (фиг. 5, А), Нее пять переходов дадут одну-единственную линию поглощения.
Если, однако, ион железа или марганца входит в состав кристалла или молекулы, то он будет испытывать действие внутренних электростатических полей; при этом вступит в действие эффект Штарка и так же, как в случае триплетного состояния, произойдет расщепление энергетических уровней. Величина расщепления опять-таки зависит от симметрии и напряженности внутренних нолей, но при этом остается справедливым то же самое общее правило: электрическое поле с осевой симметрией само по себе не может снять двойное вырождение состояний, которые характеризуются квантовыми числами, различающимися только знаком. Действие внутреннего поля будет поэтому таким, как показано слева на фиг. 7, Б, т. е. в нулевом магнитном поле произойдет электронное расщепление и возникнут три уровня, соответствующие квантовым числам ±1/2, ±3/г и ±5/2. Наложение внешнего магнитного поля снимает это двойное вырождение, и по мере увеличения поля уровни все больше расходятся. При достаточно высокой напряженности внешнего магнитного поля уровни располагаются последовательно в порядке, указанном на фиг. 7, Б. В этом случае разрешенные переходы между ними имеют место при разных значениях внешнего магнитного поля, и потому наблюдаются пять отдельных линий поглощения. Расстояние между этими линиями непосредственно отражает величину расщепления в нуле - пом магнитном поле под влиянием электростатических внутренних полей, и поэтому его можно использовать в качестве меры этого расщепления (так же как и в случае триплетного состояния).
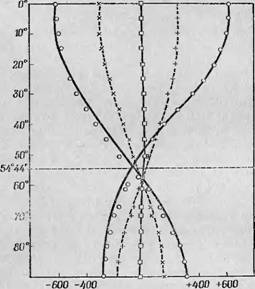
Описывая изменения энергетических уровней в зависимости от величины прилагаемого поля, мы, как и в предыдущем разделе, ве учитывали эффекты второго порядка и конкуренцию между электрическим и магнитным полями за эффективную ось квантования. По мере перехода к слабым магнитным полям энергетические уровни ведут себя более сложно, но это имеет значение только в области очень слабых полей. Как и в случае триплетного состояния, здесь имеет место сильная угловая зависимость электронного расщепления, и положение пяти переходов будет заметно изменяться с изменением угла между внешним магнитным полем и направлением внутреннего электростатического поля. В первом приближении это изменение будет описываться функцией (3cos20—4), как обычное диполь-дипольное взаимодействие. Такой характер угловой зависимости виден вполне отчетливо на фиг. 8, где приведены экспериментально полученные кривые, характеризующие положение пяти линий, соответствующих пяти электронным переходам, для соли марганца при длине волны 3,2 см и значениях магнитного поля порядка 3000 Э. Такие магнитные поля недостаточно велики для того, чтобы уменьшить упомянутые выше эффекты второго порядка до пренебрежимо малой величины, и потому экспериментальные точки нестрого
|
Величинг расщепльлия, Э >т?*ловая завпсимость Ьлектроп'иош расщеплепия Ндалюдаемое в экйгернменте расЭЯпленце для Мп2+ при Д1&ше волны 3 см [румерения йроводилйс§> на фторосЬликпте марганца. |
[ложатся на кривую функции (3 cos2 0 — 1). Однако основные закономерности выявляются на графике достаточно ясно (в частности, почти полное исчезновение расщепления при 0 = 54°44', гаогда выражение (3cos20 — 1) обращается в нуль).
Подробное изложение теории электронного расщепления с учетом эффектов второгс порядка и других факторов монщо найти в книге Ассенгейма ([1], стр. 37). В гл. 6 мы на примере металло - органических соединений несколько подробнее обсудим вопрос о том, какую информацию может дать изучение такого электронного расщепления в нулевом поле.
I.ti. Сверхтонкое расщепление и его происхождение