Электронный Парамагнитный резонанс в биологии

Чувствительность спектрометров

Прежде чем обсуждать схему более совершенных ЭПР-спектро - метров, рассмотрим основные факторы, определяющие чувстви­тельность любого спектрометра. При исследовании спектров ЭПР биохимических и биологических систем чувствительность может явиться одним из самых важных лимитирующих факторов, эксперимента. Так, если объект исследуется в условиях, близких к условиям in vivo, то, как правило, приходится иметь дело с раз­бавленными растворами изучаемых соединений и концентрация неспаренных электронов оказывается очень низкой. Кроме того, сигнал ЭПР в биологических объектах существенно ослабляется из-за присутствия воды, всегда входящей в качестве раствори­теля в состав объекта. Вода обладает высокой диэлектрической проницаемостью, и переменное электрическое поле характери­зуется большими диэлектрическими потерями. Поэтому при изу­чении водных растворов их необходимо помещать в специальные кюветы, расположенные так, чтобы образец заведомо находился вне области электрического микроволнового поля.

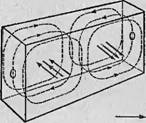
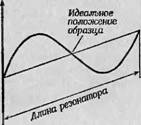
На фиг. 16 показано распределение магнитного и электриче­ского полей в простом прямоугольном резонаторе, чахце всего используемом в ЭПР-спектрометрах. Можно видеть, что линии переменного микроволнового магнитного поля концентрируются в центре полости резонатора и направлены здесь вертикально вниз. Именно в этом месте и помещается кювета с образцом. Максимумы напряженности электрического поля располагаются на расстоя­нии четверти длины волны по обе стороны от этой точки. При колебаниях такого простого основного типа силовые линии элек­трического поля перпендикулярны широким стенкам волновода. Амплитуда колебаний этого поля уменьшается по мере удаления от точек максимума и проходит через нулевое значение как раз в точке максимума магнптпого поля (фиг. 16, Б). Однако даже на очень небольшом расстоянии от центральной зоны электри­ческое поле уже отлично от нуля, и поэтому при исследовании сред, в которых диэлектрические потерн очень велики, например водных растворов, объем образца должен быть ограничен разме­рами очень узкой области, прилегающей к центральному нуле­вому участку. Поэтому спектрометры для исследования водных образцов снабжаются, как правило, специальной плоской квар-
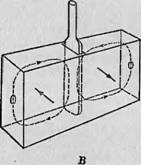
девой кюветой прямоугольной формы, расположенной перпенди­кулярно длинной оси волновода и полностью перекрывающей его сечение (фиг. 16, .В). Таким способом удается поместить мак­симальной количество образца в переменное микроволновое поле, не заходя в область электрического поля. Однако в этом случае «коэффициент заполнения», т. е. отношение объема образца,

Е

Находящегося в микроволновом поле, к общему объему, занимае­мому этим полем, гораздо меньше, чем при работе с образцами, не обладающими такими высокими потерями; это также($ значи­тельно снижает максимально достижимую чувствительность при исследовании большинства биологических объектов. По всем этим причинам при изучении водных растворов необходимо исполь­зовать спектрометры с возможно большей чувствительностью.

Другим основным параметром, опредетающим качество и при­годность спектрометра, является разрешение, т. е. минимальное расстояние между дауыя линиями поглощения, при котором их можно различить. Предел разрешения иногда определяется самим
образцом; очевидно, что в веществе, дающем широкие линии поглощения, наблюдать какие-либо тонкие детали спектра невоз­можно. В то же время при исследовании растворов многие про­цессы, приводящие к уширению сигнала ЭПР, усредняются, как упоминалось выше, до нуля, и это позволяет наблюдать очень узкие линии поглощения в спектре ЭГГР. В подобных случаях раз­решение часто лимитируется конструкцией самого спектрометра, главным образом степенью однородности магнитного поля. Если расстояние между суперсверхтонкими компонентами спектра составляет 30 мЭ или меньше, напряженность магнитного поля не должна изменяться по объему образца более чем на 30 мЭ; в про­тивном случае наблюдать индивидуальные линии будет невоз­можно. Помимо пространственной однородности внутри объема образца, магнитное поле должно быть достаточно стабильным и во времени. Так, например, если полная запись спектра зани­мает 20 с, а поле'изменяется за время записи больше чем на 30 мЭ, то спектр окажется неразрешенным и смазанным. Такие же тре­бования предъявляются, естественно, и к стабильности сверхвы­сокой частоты; если частота будет меняться в процессе записи, спектр также будет размазанным и выявить сверхтонкое расщеп­ление не удастся. Итак, разрешение в любой системе ЭПР зависит в основном от двух факторов — временной стабильности сверх­высокой частоты и магнитного поля и пространственной одно­родности магнитного поля в объеме образца. Эти факторы подробно рассматриваются в книге Уилмхэрста ([1], гл. 6), и поэтому здесь мы на них останавливаться не будем.

Обратимся теперь к определению параметров, реально опреде­ляющих чувствительность спектрометра, т. е. минимальное коли­чество неспаренных электронов, которое может быть обнаружено с его помощью. Ограничение.„чувствительности обусловливается главным образом шумами, возникающими в самой системе детек­тирования, причем основная доля шумов приходится на полу­проводниковый кристаллический детектор, находящийся в конце волноводного тракта. Следовательно, для того чтобы рассчитать предельную чувствительность спектрометра, нужно определить 1) напряжение шумов, создаваемое в детекторе, и 2) парамагнит­ную восприимчивость образца (и тем самым число имеющихся в нем неспаренных электронов), при которой сигнал поглощения даст то же напряжение, что и шумы. Если бы детектирующий кри­сталл представлял собой идеальный детектор и не давал своих собственных избыточных шумов, создаваемое на нем напряжение шума определялось бы формулой

^щум = (^о кТ • Av)1 /2, (2.1)

Где Rо— импеданс волновода, к — постоянная Больцмана, Т — абсолютная "температура, Av — используемая полоса частот.

На практике, однако, в общее выражение, характеризующее мощность шума Ршум на выходе детектора, входят шумы, обу­словленные целым рядом дополнительных причин, т. е.

^шум= (^r+^ + Fc-l) kT'HV' (2-2)

Где Nm — шум, поступающий нз волиоводного тракта; L — потери преобразования в кристалле^ FA — коэффициент шума усилителя и TD — относительная шумовая температура [1] самого кристалла.

Для определения парамагнитноМ восприимчивости (и тем са­мым — концентрации неспаренных электронов), при которой сигнал на детекторе имеет мощность, равную уровню шума, необ­ходимо сначала рассмотреть эффект поглощения в резонаторе. Поглощение микроволновой мощности! обусловлено взаимодей­ствием магнитных моментов неспаренных электронов с магнит­ным полем высокочастотных колебаний. Общее выражение для динамической восприимчивости неспаренного электрона может быть записано в виде

Х = У.'-}-%", (2.3)

Где действительная часть % отражает намагниченность, меняю щуюся в фазе с магнитным полем, а мнимая часть у"— намагни­ченность, сдвинутую по фазе относительно магнитного поля. Таким образом, если образец поместить в переменнее магнитное поле Н s'n cof, то его намагниченность будет выражаться формулой

%'Н1 sin col— '/"II, cos at.

Энергия, поглощенная при магнитном взаимодействии, опре­деляется общим вырэдкением II {DM'Dt), где М — намагничен­ность. Таким образом, чтобы получить общую мощность Ра, погло­щенную содержащимися в образце неспаренными электронами, нужно разделить полную энергию, поглощенную в течение одного периода, на длительность периода ЕяТсо:

ЖШ I щШ (2-4)

Период

Интеграл берется по этому же периоду 2эт/(о и, следовательно, 2Jt/(D 2Я,"СО

Ра = -^г j b i to sin соT [x'costo^-j x"sincoЈjЈ®,

О о

Т. е.

Ра= (2.5)

Рассмотрим влияние поглощения энергии на добротность резо­натора Q. Добротность характеризует отношение энергии, накоп­ленной в резонаторе, к энергии, рассеиваемой в результате потерь, обусловленных сопротивлением стенок резонатора, утечкой через отверстия связи или какими-либо другими причинами. В отсут­ствие резонансного поглощения добротность определяется фор­мулой

______________ Энергия, накопленная в резонаторе

^ Рассеиваемая мощность

Или

<?о = -^Цг------------------------------------------ (2.6)

И:

Где Vc— объем резонатора, а Ри, — мощность, рассеиваемая в результате утечек через отверстия связи или из-за сопротивле­ния стенок резонатора.

В результате резонансного поглощения появляются дополни­тельные потери энергии и, следовательно, добротность резонатора уменьшается; новое ее значение определяется формулой

Где интеграл в знаменателе отражает взаимодеиствие микровол­нового поля с содержащимися в образце неспаренными электро­нами (см. уравнение 2.5). Следует заметить, что в этом случае интеграл берется не по объему всего резонатора Fc, а только по объему образца Fs.

Мощность, поглощенную образцом, можно считать малой по сравнению с другими потерями мощности; тогда, разделив числитель и знаменатель на Рш и развернув полученные выраже­ния, находим, что

Ю I jjv. fiy

<?Погл = -8я J 1 (i • • •)' (2-8)

Откуда т. е.

<?nor«-<?ofl-W<?o]- (2.9)

Символ г], которым здесь обозначено отношение двух интегра­лов,— это так называемый коэффициент заполнения, показы-
вагощий, какая часть эффективного микроволнового магнитного поля заполнена образцом.

Итак, в результате поглощения, обусловленного неспаренными электронами, добротность Q уменьшается на величину

= (?о' 4лщ"; (2.10)

Относительное изменение добротности, которое можно приравнять к относительному изменению эквивалентного демпфирующего сопро­тивления В, выразится тогда следующим образом:

Щ - = -Jf = ■ Q0. (2.11)

Для того чтобы рассчитать, как изменится падение напряже­ния на детекторе в результате такого изменения добротности

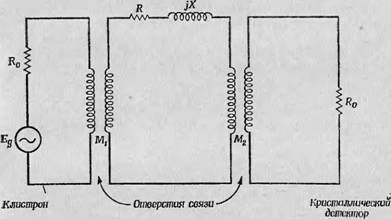
Резонатора, представим микроволновую систему в виде низкоча­стотной эквивалентной схемы. Такая эквивалентная схема для простейшего спектрометра проходного типа приведена на фиг. 17. Клистрон, являющийся источником микроволновой мощности, представлен здесь в виде генератора Eg с импедансом R0. Через отверстия связи резонатора, представленные взаимоиндуктивно­стью Ми генератор Eg связан с резонатором (центральный кон­тур схемы с омическим сопротивлением В и реактивным сопро­тивлением X). Далее мощность через второе отверстие связи Мг Поступает на кристаллический детектор (расположенное в конце схемы согласованное сопротивление В0, на котором и создается регистрируемое падение напряжения VL ). Напряжение на детек­
торе выражается через константы двух других контуров схемы следующим образом [2]:

У*-£'тя+,х+т1тш (2Л2)

-"О "о

При поглощении, обусловленном неспаренными электронами (в эквивалентной схеме это соответствует малому изменению омиче­ского сопротивление ft), напряжение VL изменяется следующим образом:

Ш т%мг

BR Efr ( , Jm{ co'W|2- (2-13)

Для обеспечения максимальной чувствительности спектро­метра выражение (2.13) должно быть максимизировано. Отсюда сразу следует, что X = О (т. е. что резонатор должен быть настроен на ^резонансные условия) и, следовательно, при опти­мальных значениях параметров связи

Со Wf _ соR 9 ,

Щ Щ 2Н0 •

Таким образом, для максимума SVL/6R получаем выражение

F>VL_ Eg

6 R 8 R

Откуда наблюдаемое изменение напряжения на детекторе, выражен­ное через изменение добротности резонатора Q, равно

6у _ ЕШ Ее Д<3 ,2,

Подставив выражение Д(?/<?0 из уравнения (2.11), получим

Или

(2.17).

Чтобы найти минимальную обнаруживаемую восприимчивость, Нужно приравнять это изменение напряжения к напряжению - Щума на детекторе, определяемому уравнением (2.1):

Т. е.

„ _ 1 / 4Л'0-А:7'-Лу I/a El ) '

Или

<2-'8>

Где Р0, заменяющее E2G/AR0,— максимальная мощность микро­волнового поля, которую можно получить от клистрона.

Следует заметить, что это выражение выведено из уравнения (2.1), относящегося к случаю, когда кристаллический детектор не обладает избыточными шумами. Однако, как уже отмечалось (уравнение 2.2), существует ряд дополнительных источников шума, которые также должны быть включены в коэффициент

Шума F, определяемый выражением

+ + (2Л9>

Выражение для минимальной обнаруживаемой восприимчивости примет тогда вид

1 /F-kT-AvVа /0 оп.

Ь...н=^0(—р—) • (2.20)

Как правило, практический интерес (особенно в биологиче­ских и биохимических приложениях ЭПР) представляет число содержащихся в образце неспаренных электронов, а не величина мнимой части парамагнитной восприимчивости, определяемая уравнением (2.20). Поэтому для оценки фактической чувстви­тельности ЭПР-спектрометра мы должны найти соотношение между числом неспаренных электронов в образце и величиной %". Но сна­чала рассмотрим соотношение между числом неспаренных элек­тронов и статической восприимчивостью, определяемой в клас­сической теории парамагнетизма.

Намагниченность, а следовательно, и восприимчивость образца определяются разни:(ей в количестве спинов, ориентиро­ванных параллельно и антипараллельно полю. Как уже было показано в гл. 1 (уравнение 1.3), отношение числа тех и других пропорционально E~HvLkT, где v — частота падающего микровол­нового излучения. Выражение Hv при резонансе можно заменить на gfiH. При Нормальных условиях' эта энергия много меньше энергии, обусловленной температурой образца и равной кТ; Следовательно, отношение GfiII/кТ мало и экспонента может быть аппроксимирована первыми двумя членами степенного ряда, т. е. выражением (1 — GfiII/кТ). Такая аппроксимация неправо­мерна для температур жидкого гелия и ниже, но для температуры кипения жидкого водорода (20 К) и выше, а следовательно, почти во всё^!'экспериментах, выполняемых на биологических образ­цах, она вполне применима. Таким образом, разницу в числен­ности между двумя группами электронов можно приравнять к (NJ2) (g^H'kT), где N0— общее число неспаренных электронов, а следовательно, число активных атомов или молекул.

В магнитном поле каждый из избыточных электронов обладает магнитным моментом 1/2 gfi вдоль направления поля, и, таким образом, существует магнитный момент, некомпенсированный другими электронами и равный (g2fi2N0-H)i(ikT). Статическую восприимчивость обоазца, отнесенную к единице массы, можно получить, разделив это выражение на величину магнитного поля, или, другими словами,

(2-21)

Подставив в уравнение (2.21) численные значения атомных кон­стант и предположив, что значение ^-фактора близко к значению G- фактора свободного электрона (это справедливо для всех образцов, содержащих свободные радикалы), получим следующее соотношение между N0— общим количеством неспаренных элек­тронов в образце — и статической восприимчивостью:

-А^ = 1,60 • 1024 • 71 • Xoi (2.22)

Где %0 выражено в электромагнитных единицах CGS.

Итак, мы получили выражение, связывающее число неспарен­ных электронов в образце со статической восприимчивостью. Сле­дует заметить, что при выводе этого выражения рассматривались только электроны, распределенные между двумя возможными энергетическими уровнями и, следовательно, обладающие спи­ном S = 1/2. Это, как правило, верно для всех биологических ибразцов, за исключением те[х, которые содержат ионы элементов переходной группы, где на атом может приходиться не один, а несколько неспаренных электронов. Нетрудно модифицировать общую теорию парамагнитной восприимчивости таким образом, чтобы распространить ее и на эти случаи, так как создаваемое магнитным полем распределение электронов между (2S fj 1) различными уровнями можно подсчитать с тем же приближением, что и раньше. Значения намагниченности, создаваемой каждым из этих уровней, можно просуммировать и получить окончатель­ный результат для всех возможных проекций магнитных момен­тов. Выражение для статической восприимчивости, отнесенной к единице массы, принимает тогда более общий вид [3]

(2.23)

Дальнейшие расчеты в этой главе мы будем, однако, проводить в предположении, что в рассматриваемом образце имеется только один неспарзьный электрон на атом или молекулу и, следова­тельно, можно пользоваться уравнениями (2.21) и (2.22) [хотя при лкелании те же рассуждения можно провести и для более общего случая, представленного уравнением (2 23)1-

Последний этап расчета состоит в том, чтобы, получить соотно­шение между статической восприимчивостью ул и величиной %". Следует напомнить, что впервьм поняти^комплексной восприим­чивости было введено при рассмотрении количества поглощен­ной микроволновой мощности. Эту последнюю можно также найти, рассматривая фактическое число электронных переходов между двумя состояниями. Так, было показано, что для простого слу­чая, когда на атом или молекулу приходится один неспаренный электрон, разница в заселенности двух уровней равна

И каждый из переходов между уровнями сопровождается погло­щением кванта энергии Tt со, где со ■— угловая частота и h = h/2n. Следовательно, результирующая величина микроволновой мощ­ности, поглощенной при переходах между этими двумя уровнями, равна

Т, Щ /г2-ш2 /о о N

= ■■- kf--Pm- (2.24)

Здесь

Pm=Il. y2.Hl-g(iо-со0), (2.25)

ТЩу— гиромагнитное отношение для электрона, равное Tt, A g (го — со0) — функция, описывающая форму линии поглощения (уравнение 1.6). Объединив уравнения (2 24) и (2.25), получаем

Щ11• <® " юо)- (2.26)

Если воспользоваться уравнением (2.21), то можн®» записать /'аос в виде

= (2.27)

Приравняь это выражение к выражению (2.5), полученному ранее; когда впервые было введено понятие комплексной восприимчи­вости, получим, что

(со — «Во). (2.28)

Вспомним теперь о параметре Т2, определяемом уравнением (1.9); в разд. 1.3.2 было показано, что величина, обратная этому параметру, служит мерой ширины линии поглощения. Ширину линии, А(о, можно, таким образом, представить в виде 1/л-£макс, ГДе йиакс — максимальное значение функции G (со — ю0) при резонансной частоте со0. Из этого следует, что при достижении резонансной частоты уравнение (2.28) принимает вид

'' = Хо Ш ' (2-29)

X

И если это уравнение объединить с уравнением (2.21), то мы полу­чим окончательное выражение для отношения между комплексной восприимчивостью и содержанием неспаренных электронов в об­разце:

Подставив, наконец, в это уравнение правую часть уравнения (2.20), в котором минимальная обнаруживаемая восприимчивость выражена через фактические параметры ЭПР-спектрометра, полу­чаем следующее окончательное уравнение:

ТО-Н= Т ОБразца • ^ '^Ь) ' ([

Образец Условия Резонатор Детектирующая

Резонанса система

Уравнение (2.31) дает строгое соотношение между минималь­ным числом неспаренных электронов, которое может быть обна­ружено в образце, и практическими параметрами всей системы ЭПР-спектрометра. Эти параметры разделены на четыре основные группы. В первую группу входят атомные константы и темпера­тура образца (как правило, она отличается от температуры детек­тора, включенной в состав четвертой группы). Вторая группа включает резонансную частоту со0 и ширину линии А си (первый параметр определяется условиями эксперимента, а второй — свойствами самого образца). В третью группу входят добротность и коэффициент заполнения — параметры, связанные исключи­тельно со свойствами резонатора. Параметры четвертой группы характеризуют свойства детектирующей системы; к этой же груп­пе относится и фактическая мощность, проходящая через спектро­метр. Теперь можно рассмотреть влияние каждой из этих групп параметров на предельную чувствительность спектрометра и ука­зать пути обеспечения максимальной чувствительности в каждом конкретном случае.

А. Понижение температуры образца

Очевидно, что температура образца — это единственный под­дающийся изменению параметр из первой группы в уравнении (2.31), и если сделанное в начале расчета приближение право­мерно, то с понижением температуры чувствительность будет линейно увеличиваться. Могут существовать также и иные мотигы для понижения температуры образца, например необходи­мость уменьшения ширит: линии A to. В то же время некоторые эксперименты желательно проводить при комнатной температуре; в особенности это относится к биологическим и биохимическим исследованиям, где условия должны быть как можно ближе к условиям in vivo. Поэтому в таких случаях возможность повы­шения чувствительности^а счет снижения температуры образца по большей части исключена.

Б. Повышение резонансной частоты

Если по-прежнему считать, что принятые допущения верны, то чувствительность спектрометра должна линейно расти с повйт! шением резонансной частоты (на практике чувствительность растет быстрее, так как с повышением со0 растут и некоторые другие параметры, например добротность резонатора). Из этого следует, что измерения на более высоких частотах всегда будут давать более высокую абсолютную чувствительность, и это одна из при­чин, по которой исследования на монокристаллах, как правило, лучше проводить в диапазоне 8 мм (^-диапазон), чем в диапазоне 3 см (Х-диапазон).

Как ужё| говорилось, магнитное поле в 13 ООО Э, необходимое для работы в ^-диапазоне'являлось раныые^верхним пределом, ограничивающим дальнейшее повышением частоты. С появлением сверхпроводящих магнитов положение в корне изменилось, и в настоящее время негр) недостатка в работах, выполняемых ь диапазоне 4 или даже?«2 мм, где чувствительность спектрометра при исследовании малых кристаллов (каковыми в ряде случаев являются биологические образцы) можно значительно повысить. Подробное рассмотрение таких сверхвысокочастотных спектро­метров проведено в разд. 3.6, и потому здесь мы не будем спе­циально останавливаться на них.

В. - Уменьшение ширины линии поглощения

Совершенно ясно (даже и без уравнения 2.31), что при одной и той же интегральной интенсивности узкую линию поглощения обнаружить легче, чем широкую,, и что, следовательно, между А со Й чувствительностью спектрометра должна существовать прямая зависимость. Однако ширина линии, как правило, определяется свойствами самого образца и экспериментатор не может изменять ее по своему усмотрению; лишь в некоторых случаях А со можно уменьшить путем охлаждения образца и тем самым повысить чувствительность.

Г. Увеличение добротности резонатора

Увеличение добротности резонатора непосредственно влияет на чувствительность спектрометра, и поэтому при изготовлении резонаторов стремятся добиться максимально высокой степени точности и идеальной полировки поверхности. Добротность резо­натора можно также несколько повысить путем серебрения или золочения его внутренней поверхности. Следует помнить, что при введении в резонатор образца эффективное значение доброт­ности заметно понижается; поэтому очень важно сконструировать резонатор таким образом, чтобы его добротность была возможно более высокой.

Д. Увеличение коэффициента заполнения

Коэффициент заполнения по существу служит мерой того, насколько удачно расположен образец в микроволновом магнит­ном поле. Для обеспечения высокого коэффициента заполнения необходимо тщательно продумать геометрическую конструкцию держателя или кюветы. При этом, однако, часто приходится идти на компромиссные решения, так как если образец попадает в область электрического микроволнового поля, то это приводит к большим электрическим потерям (об этом уже говорилось при рассмотрении водных растворов; см. фиг. 16). Таким образом, увеличение коэффициента заполнения часто лимитируется мак­симальным размером кюветы, допустимым с точки зрения элек­трических потерь. Надо также заметить, что при большом коэф­фициенте заполнения часто заметно снижается добротность, так что на самом деле параметром, величины которого необходимо максимизировать, является произведение Qr■

Е. Повышение уровня микроволновой мощности

Чувствительность спектрометра (в отсутствие насыщения об­разца) пропорциональна корню квадратному из мощности падаю­щего излучения, которая целиком определяется выходной мощ­ностью клистронов; это необходимо иметь в виду при конструи­ровании спектрометра. Следует, однако, заметить, что чрезмерное повышение уровня микроволновой мощности при исследова­нии биологических объектов приведет к появлению эффекта насы­щения и связанного с ним уширения сигнала ЭПР, так что чув­ствительность не может увеличиваться беспредельно за счет уве­личения мощности. Эффекты уширения, вызванные насыщением, подробно рассмотрены в разд. 3.7.

Ж. Понижение уровня шумов детектора

Различные факторы, регулирующие уровень избыточного шума в системе детектирования, уже вкратце упоминались выше и были суммированы в уравнении (2.2). Мы подробно обсудим их в следующем разделе, так как на практике именно они огра­ничивают чувствительность спектрометра. В том же разделе рас­смотрены методы уменьшения различных форм избыточного шума.

З. Сужение полосы пропускания детектирующей системы

Из уравнения (2.31) можно видеть, что в принципе чувстви­тельность спектрометра можно неограниченно увеличивать, умень­шая ширину полосы пропускания, A-v, детектирующей системы. При таком сужении полосы необходимо обеспечить высокую по­стоянную времени спектрометра, а следовательно, и высокую временную стабильность всех его блоков. Это основное требование, предъявляемое к любому ЭПР-спектрометру, объясняет, почему приходится уделять столько внимания стабилизации магнитного поля и микроволновой частоты. Если эти параметры удается достаточно хорошо стабилизировать, можно добиться значитель­ного повышения чувствительности, удлиняя время записи и поль­зуясь схемами с очень узкой полосой пропускания. Постоянную времени можно увеличить за счет интегрирования большого числа повторяющихся быстрых временнйх разверток, что зачастую более удобно с практической точки зрения. Методы усреднения будут подробно рассмотрены в разд. 3.2, так как они представ­ляют собой одно из последних и наиболее важных достижений современной экспериментальной ЭПР-спектроскошш.